1から9までの二つの数を加え合わせる計算は,四則計算の基礎になるものである。したがって,計算についての理法がわかったら,その計算が反射的にできるようにしなければならない。このような意味から,この種の計算を,加法九々ということにした。減法九々は,減数差が,ともに,1から9までの数になる計算である。しかし,加法九々,減法九々は,決レて乗法九々のように,呼び声としてのものではない。
b)単位分数
5/6は,1/6 単位として数えて,5に当たるものである。すなわち,5/6は1/6の5倍である。このように考えると,1/6は6を分母とするあらゆる分数の単位であるとみられる。そこで,分母が整数で,分子が1である分数を,特に,単位分数ということにした。
c)正方形グラフ・帯グラフ
これは,ともにグラフの一種である。
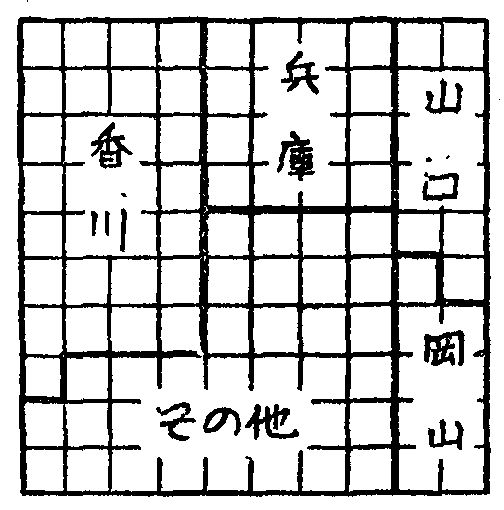
正方形グラフ(第1図参照)は,正方形を100個の小さな正方形に等分し,全体に対する各部の割合を,その小さな正方形の個数で示すことにして作られたものである。
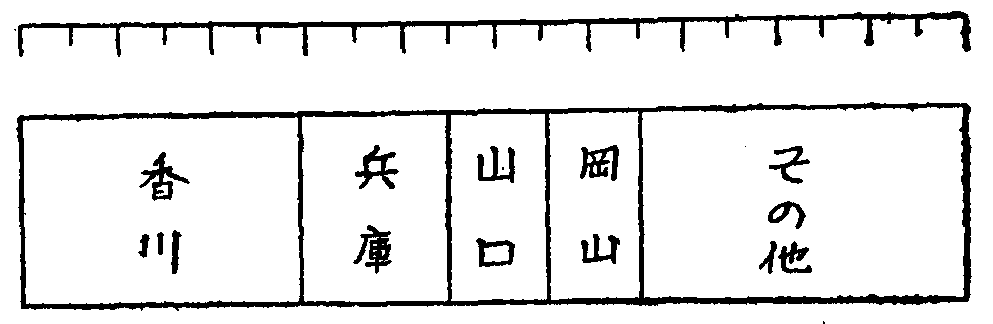
帯グラフ(第2図参照)は,矩形グラフともいわれたものである。矩形の矩は当用漢字にはないため,矩形グラフを帯グラフということにした。帯グラフは,全体に対する各部の割合を,帯の長さで示すことにして作られたものである。
第1図
わが国における塩の生産能力
(昭和二十一年四月統計)
総量 500,000㎏
第2図
わが国における塩の生産能力
(昭和二十一年四月統計)
総量 500,000㎏
d)台形
梯形の梯は,当用漠字にないために,梯形を台形ということに一応定め,一般からの意見を求めることにした。
e)一段階の問題・二段階の問題
一段階の問題の例;えんぴつを2本もっています。きょう,おかあさんから3本いただきました。みんなで,なん本になったでしょう。
二段階の問題の例;ひろしくんの家で,大工さんをたのみました。おとうさんが6日間の賃金として,900円支払われました。この割合で,あと30日間の賃金を支払うのだそうです。いくら支払うことになりますか。
四則のどれか一つの計算で,すぐに解決できる問題を,一段階の問題ということにした。四則計算の二つを組み合わせて解決できる問題を,二段階の問題ということにした。但し,加法と加法というように,同じ種類のものを組み合わした問題も含まれる。
f)一次元の表・二次元の表
一次元の表(第3図参照)は数が縦,あるいは横の一方にだけ並んでいる表のことである。二次元の表(第4図参照)は,数が,縦にも横にも,並んでいる表のことである。
第3図
昭和22年度の東京都内における小学生交通事故の表(警視庁交通課調査)