第１　目　　標

１　数量や図形に関する基礎的な概念や原理・法則の理解を深め，より進んだ数学的な考え方や処理のしかたを生み出す能力を伸ばす。

２　数量や図形に関して，基礎的な知識の習得と，基礎的な技能の習熟を図り，それらを的確かつ能率的に活用できるようにする。

３　数学的な用語や記号を用いることの意義について理解を深め，それらによって，数量や図形についての性質や関係を簡潔，明確に表現したり，思考を進めたりする能力を伸ばす。

４　ものごとを数学的にとらえ，その解決の見通しをつける能力を伸ばすとともに，確かな根拠から筋道を立てて考えていく能力や態度を養う。

５　数学が生活に役だつことや，数学と科学・技術との関係などを知らせ，数学を積極的に活用する態度を養う。

以上の目標の各項目は，相互に密接な関連をもって，全体として数学科の目標をなすものであるから，指導にあたって，この点を常に考慮しなければならない。

第２　各学年の目標および内容

〔第１学年〕

１　目　　標

(１)　整数，小数および分数を数として統一的にとらえさせ，その取り扱いに習熟させる。さらに数を正の数，負の数にまで拡張して，数の概念の理解を深め，これらの数を用いて数量を統一的に表現し，処理する能力を養う。

(２)　文字を用いて数量についての関係や法則を一般的にしかも簡潔に表現して，ものごとを考察し，処理する能力を養う。

(３)　比についての理解を深め，その取り扱いに習熟させる。また，事象の変化について，これを数量的にとらえ，変数や対応の考え方や見方をしだいに伸ばし，各種の数量関係を見いだす能力を養う。

(４)　計量の意義や方法についての理解を深めるとともに，基本的な図形の面積や体積を求める能力を伸ばす。

(５)　図形について，基本的な操作に慣れさせる。また，これらの操作や計量などを通して，基本的な図形について相互の関係や性質の理解を深め，図形の観念を豊かにする。特に，空間図形と平面図形との関連を明らかにする。

　Ａ　数

(１)　四則についての相互関係や法則が，整数，小数および分数を通じて変わらないことなどについて理解を深める。

(２)　整数の約数と倍数についての性質を明らかにし，分数などの計算に習熟させる。

(３)　正の数，負の数を用いると，式がより広い意味に用いられることを理解させるとともに，これらの数の四則計算に習熟させる。

(４)　場面に応じて，適切な近似値の取り扱いができるようにする。

ア　誤差や有効数字の意味と近似値の表わし方。

イ　計算尺による乗法と除去。

加法，減法，乗法，除法，四則，逆数，累乗，２乗，平方，３乗，立方，指数，交換法則，結合法則，分配法則，偶数，奇数，素数，公約数，公倍数，最大公約数，最小公倍数，正の数，負の数，符号，正の符号（＋），負の符号（−），絶対値，項，数直線，不等号，＞，＜，誤差，近似値，有効数字

(１)　文字を用いて，数量およびその間の関係や法則を式に表現することができるようにする。
ア　式の中の文字は，数の代わりの記号であること。

イ　式の中の文字に，数値を代入して式の値を求めること。

ウ　文字を用いた式における乗除の表わし方の規約。

(２)　等式において，値のわからない文字が一つのとき，その文字の１位を，逆算で求める能力をいっそう伸ばす。

式の値，代入

(１)　比および比例式についての理解を深め，その取り扱いに習熟させる。
ア　比の三用法の相互関係

イ　利率，指数など社会で用いられている各種の比率の意味。

ウ　連比および比例式の意味ならびに比例式の基本的な性質。

(２)　伴って変わる二つの量の関係を，グラフや式などに表わしてその特徴を見いだし，これを用いることができるようにする。
ア　二つの量の関係を表やグラフに表わすことおよびその変化の特徴。

イ　式の形の上からみた比例および反比例の特徴。

単利，復利，元金，利率，期間，利息，日歩，元利合計，指数（割合に関するもの。），連比，比例配分，比例式，比例定数

(１)　測定の意味の理解を深め，測定には必ず誤差を伴うことを明らかにする。

(２)　単位系の理解を深め，メートル法の長所を活用できるようにする。

ア　メートル法の単位が，基本単位と誘導単位からできていることおよびそれらの単位の間の関係。

イ　メートル法と尺貫法およびヤードポンド法との単位の関係ならびに表またはグラフを用いて換算すること。

ウ　現行計量制度についての知識。

(３)　図形の計量についての能力を伸ばす。
ア　小学部で学習した各種の基本図形についての求積公式の理解を深めることおよび球やすい体の求積公式を知り，これらを用いること。

イ　円における中心角と弧との関係およびおうぎ形における中心角と面積との関係を知り，これらを用いること。

ウ　図形を基本的な図形に分解して，その図形の面積や体積を求めること。

π，メートル毎秒，ｍ／Ｓ，キロメートル毎時，km／ｈ（はたはkm／時）

(１)　基本的な作図についてくふうさせ，これらを通して平面図形の概念や性質を明らかにする。
ア　平行線，角の二等分線，垂線，線分の垂直二等分線などの作図。

イ　各種の三角形と四角形の作図およびそれらを決定する要素と性質。

ウ　二直線の位置関係と平行線の性質。

エ　図形を基本的な図形に分解し考察すること。

オ　三角形や多角形の角についての性質。

(２)　直線図形の間の特殊一般の関係について理解を深める。
ア　三角形の種類とその相互関係。

イ　四角形の種類とその相互関係。

(３)　空間図形の中に平面図形を見いだしたり，平面図形から空間図形を構成したりする操作に親しませ，図形の概念を明らかにする。
ア　直線と直線との位置関係，平面と平面との位置関係および直線と平面との位置関係ならびにその基本的な性質。

イ　基本的な立体図形の展開図と性質。

ウ　基本的な立体図形の投影図または断面と性質。

エ　平面図形の運動（回転移動と平行移動）によって空間図形ができることおよびこれらと関連した円柱，円すい．球などの性質。

(４)　回転や対称の見方に親しませ，これらによって新しい図形を作ったり，図形の性質を明らかにしたりする。
ア　ある図形と対称な図形の作図。

イ　二等辺三角形，長方形，正方形，正多角形などの性質。

ウ　円の性質や円と直線との位置関係およびこれらを球の性質や球と平面との位置関係などに拡張すること。

線分，半直線，中点，二等分線，垂線，上，平行線，//，距離，分（′），秒（″），対頂角，錯角，同位角，∠，∠Ｒ，鋭角，鈍角，余角，補角，頂角，底角，内角，外角，斜辺，△，鋭角三角形，鈍角三角形，

正多角形，弧，弦，弓形，接点，接線，内接多角形，外接多角形，平面，ねじれの位置，正三角すい，正四面体，平行六面体，角すい台，円すい台，母線，正多面体，大円，小円，投撮図，基線，平画面，立画面，側画面，平面図，立面図，側面図，点対称，線対称，面対称

(１)　Ａ(４)イの計算尺については，乗法と除法の計算に利用される器具であることを知る程度とする。

(２)　Ｂ(２)の等式については，主としてすでに公式としてわかっているものや立式の容易なものを扱う。

(３)　Ｃ(１)アの比の三用法については，歩合，百分率などの各種の比率を含めて扱うものとする。

(４)　Ｃ(２)の伴って変わる二つの量の数量関係については，主として具体的な量を扱う。

(５)　作図については，定木とコンパスに限らず，必要に応じて分度器やものさしなどの用具を使用させる。

１　目　　標

(１)　正の数，負の数の理解を深め，それらを式やグラフの取り扱いに活用する能力を伸ばす。

(２)　文字は，数と同じように取り扱えることを理解させ，式の基本的な操作に習熱させる。また，文字を用いることにより，数量的な関係を，一般的にしかも手ぎわよく処理する能力を伸ばす。

(３)　一次や比例の関数関係を式やグラフに表わし，それらの特徴を理解させる。また，そのようなことを通して，変数や対応の考え方や見方を深め，見通しをもって，数量的な関係を処理する能力を伸ばす。

(４)　合同，相似などの図形の性質を活用して，直接測定が困難なものの測定をくふうしたり，能率のよい測定方法を考えたりする能力を伸ばす。

(５)　合同や相似の概念を明らかにし，それらに基づいて図形の基本的な性質を明確にする。また，図形に対する直観的な見方や考え方をさらに伸ばすとともに，論証の意義や方法について理解させ，論理的に筋道を立てて考える能力を養う。

　Ａ　数

　前学年に引き続いて，正の数，負の数の理解を深め，これらの四則計算にいっそう習熟させる。

　Ｂ　式

(１)　文字および文字を用いた式の意味の理解を深め，数量や数量の間の関係を表現する能力をいっそう伸ばす。
ア　文字で表わされた式を一つの数とみること。

イ　式の中の文字を変数としてみること。

ウ　等式の中のある文字を未知数としてみること。

エ　未知数として一つの文字を用いて，数量の間の関係を方程式に表わすこと。

オ　未知数として二つの文字を用いると，数量の間の関係が方程式に表わしやすくなること。

カ　式が表わす関係は，用いる文字にはかかわりなく，式の形のみに依存すること。

キ　文字を用いて数量の間の関係を表わしたとき，文字のとりうる値の範囲に制約のあること。

(２)　文字および文字を用いた式が，数と同じように操作できることを理解させ，次の計算に習熟させる。
ア　単項式の四則。

イ　多項式の加法と減法。

ウ　多項式と単項式との乗法。

エ　多項式を単項式で割る除法。

(３)　等式の性質を理解させ，これを用いて方程式を解くことができるようにする。
ア　一元一次方程式の解法およびこれを用いて問題を解くこと。

イ　数係数の簡単な連立二元一次方程式の解法およびこれを用いて簡単な問題を解くこと。

項（式に関するもの），単項式，多項式，同類項，係数，一次式，二次式，等式，方程式，一次方程式，根，解く，未知数，左辺，右辺，両辺，移項，連立方程式，消去，代入法，加減法

(１)　座標や式のグラフの概念を理解させ，簡単な関数関係をグラフに表わし，関数関係を明確にする。
ア　ｙ＝ａｘ，ｙ＝ａｘ＋ｂおよびｙ＝ａ／ｘのグラフ。（数係数の場合）

イ　グラフにおける式の係数の意味。

(２)　比例関係および一次の関係の特徴を式の形や計算を通して明らかにし，これを用いることができるようにする。
ア　一次の関係と比例との関連ならびに一次の関係の特徴。

イ　反比例の関係は逆数に比例する関係ともみられることおよび一般の比例関係の特徴。

ウ　実験，実測などの結果を表わす直線のグラフから，その式を求めること。

(３)　必要に応じて，公式の中のある文字を変数，他の文字を定数とみなして，比例関係や一次の関係を見いだすことができるようにする。

変数，定数，座標軸，原点，ｘ軸，横軸，ｙ軸，縦軸，ｘ座標，ｙ座標，一次関係（一次凾（かん）数），傾き（こうばい），切片，双曲線，２乗に比例，３乗に比例，２乗に反比例．積に比例

(１)　適当な縮図を用い，直接測定の困難な量を測定することができるようにする。
ア　簡単な縮図を用いて，高さ，距離，方向などを求めること。

イ　縮図が種々の場面に応用されることを知ること。

仰角，ふ角

(１)　図形の合同の概念を明確にし，三角形の合同条件を理解させ，これを用いることができるようにする。
ア　平面図形についての合同の意味。

イ　三角形の合同条件と，これから導かれる簡単な図形の性質。

(２)　図形の相似の概念を明確にし，三角形の相似条件を理解させ，これを用いることができるようにする。
ア　平面図形についての相似の意味。

イ　三角形の相似条件と，これから導かれる簡単な図形の性質。

ウ　二つの図形が相似の位置にあることの意味および図形を拡大，縮小すること。　

エ　相似形の相似比と面積比との関係。

オ　簡単な立体図形についての相似の意味およびその相似比と体積比との関係。

(３)　　図形についての研究方法として，論証を用いる意義や方法の理解を図り，論理的に筋道を立てて考えることができるようにする。
ア　帰納や類推の方法によって，推測した図形の性質が正しいかどうかを確かめるには，根拠とすることがらや用語の定義が明確であり，推論の筋道が論理的に正しいことが必要であること。

イ　論証における仮定と結論の意味。

(４)　次のような図形の基本的な性質を明らかにし，これを用いることができるようにする。
ア　三角形の基本的な性質。（直角三角形と二等辺三角形の中線についての性質や一般の三角形について内心，外心および重心が存在することなど。）

イ　平行線に関する線分の比例についての性質およびこれらの平行平面への拡張。

ウ　平行四辺形の基本的な性質およびこれから類推される平行六面体の性質。

合同，≡，合同条件，相似，∽，相似条件，内分，外分，対応（合同と相似に関するもの），相似の中心，相似の位置，相似比，定義，定理，証明，仮定，結論，中線，重心，内心，外心

(１)　Ｂ(３)アにおける文字係数の一元一次方程式については，公式の変形に関連して必要なものを取り扱う程度とする。

(２)　Ｃの「用語と記号」に示した「傾き」の代わりに「こうばい」を用いてもよいが，いずれか一方を用いる場合には，他方の表記を指導しておく必要がある。

(３)　Ｄ(１)については，実測などの作業は必要最少限にとどめ，そのもとになっている数学的な原理を明らかにすることを重視する。

(４)　Ｅ(３)の図形についての論証とは，それ以前に学んだ図形の基本的な性質を根拠にして，種々の性質を演えき的な推論によって導くことを意味する。また，論証の対象としての図形の性質については，主として基本的で平易なものを扱う。

(５)　Ｅ(４)アの三角形の基本的な性質については，その一部を第３学年において扱うことができる。

１　目　　標

(１)　数の平方根を理解させ，これまでの有理数と合わせて，数の概念の理解を深める。また，これらの数を用いて数量の処理ができるようにする。

(２)　式を扱いやすい形に変形する方法や乗法公式などを理解させ，見通しをもって式を収り扱う能力を養う。

(３)　式やグラフで関数関係を表わすことの理解を深め，簡単な二次関数の特徴や関数と方程式との関係を理解させ，見通しをもって数量的な関係を処理する能力を伸ばす。また，統計的事象について，度数分布を考えてその傾向をとらえる能力を伸ばす。

(４)　三角比や三平方の定理が，計量において果たす役割について理解させ，これらや式の変形などを活用して，計量がいっそう能率よく，しかも詳しくできるようにする。

(５)　図形の性質の理解を深め，計量的に扱う能力や与えられた条件を満たす図形を求める能力を養う。図形について，見通す力や論理的に考える力をいっそう伸ばすとともに，論理の過程を正確に表現する能力を養う。

　※のついたものは選択教科としての数学の内容とする。

　Ａ　数

(１)　数の平方根の意味とその必要を理解させ，これを用いることができるようにする。
ア　数の平方根には有理数でないものがあること。

イ　根号を用いて種々の量を式で表わすこと。

ウ　平方根表を用いて，数の平方恨を求めること。

※(２)　数の平方根について，次の計算法則を明らかにし，これを用いることができるようにする。
√ａ√ｂ＝√ａｂ

平方根，根号，√，有理数，無理数

(１)　式の計算にいっそう習熟させるとともに，基本的な乗法公式を利用できるようにする。
ア　多項式と多項式との乗法。

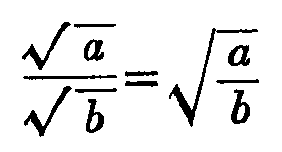
イ　次の乗法公式を用いる式の展開と因数分解。

(ａ＋ｂ)^２＝ａ^２＋２ａｂ＋ｂ^２

(ａ−ｂ)^２＝ａ^２−２ａｂ＋ｂ^２

(ａ＋ｂ)(ａ−ｂ)＝ａ^２−ｂ^２

(ｘ＋ａ)(ｘ＋ｂ)＝ｘ^２＋(ａ＋ｂ)ｘ＝ａｂ

※(ａｘ＋ｂ)(ｃｘ＋ｄ)ａｃｘ^２＋(ａｄ＋ｂｃ)ｘ＋ｄｂ

※(２)　式を文字で置き換える方法を理解させ，これを式の計算に利用できるようにする。

※(３)　分数式は，分数と同じような計算のしかたで計算できることを理解させ，簡単な分数式の四則計算ができるようにする。

(４)　次のような数係数の二次方程式について，その必要性や解き方を知らせる。

ａｘ^２＋ｂ＝０（ａ，ｂは整数で，実根をもつ場合。）

ｘ^２ｐｘ＋ｑ＝０（ｐ，ｑは整数で，実根をもつ場合。）

※(５)　二次方程式の必要性を知らせ，一般の二次方程式（係数は有理数で，実根をもつもの。）が解けるようにする。

(６)　連立方程式の理解を深め，数係数の連立二元一次方程式を用いて問題を解くことができるようにする。

※(７)　未知数を適当にとって連立一次方程式をたてる能力を伸ばし，問題をうまく解くことができるようにする。

ア　未知数の数と方程式の数との関係。

イ　連立三元一次方程式が連立二元一次方程式と同じ考え方で解けること。

ウ　数係数の簡単な連立三元一次方程式の解法。

展開，因数，因数分解，二次方程式

(１)　簡単な二次関数のグラフについて理解を深め，これを用いることができるようにする。
ア　ｙ＝ａｘ^２およびｙ＝ａｘ^２＋ｂのグラフ。（数係数の場合。）

イ　「ア」のグラフの特徴および係数と形との関係

ウ　「ア」に掲げる二次関数と一次関数との値の変化のしかたの違い。

エ　「ア」のグラフを用いた二次方程式の解法。

(２)　一つの二元一次方程式は，二つの変数の間の関数関係ともみられることを理解させ，この関係をグラフに表わすことができるようにする。また，方程式をグラフに表わすことによって，連立方程式を解くことについて理解させる。

※(３)　式のグラフの見方，作り方の理解を深めて，簡単な数係数の二次三項式のグラフをかき，これを用いることができるようにする。

(４)　資料を整理し，表，グラフ，代表値などを用いて，その資料の傾向を知ることができるようにする。

ア　度数分布の意味とヒストグラムの見方。

イ　代表値の意味。

ウ　簡単な場合の相関表や相関図の見方。

二次関数（二次函数），放物線，度数，分布，階級，ヒストグラム，代表値，相関図，相関表

(１)　鋭角についての三角比の意味を理解させ，三角比に関する計算ができるようにする。
ア　正接，正弦および余弦の意味。

イ　三角比の表の使い方。

(２)　三角比を用いて数量の間の関係を式に表わし，これを用いることができるようにする。
ア　直角三角形の辺と角との関係。

イ　三角比を用い表て三角形の面積などを計算すること。

(３)三角比相互の基本的な関係を理解させ，これを用いることかできるようにする。

三角比，正接，tan，正弦，sin．余弦，cos

(１)　三平方の定理を理解させ，これを図形の性質の考察や計量に用いることができるようにする。
ア　三平方の定理。

イ　平面図形や空間図形について，三平方の定理を用いること。

※ウ　線分の投影図から，その実長を計算や作図により求めること。

(２)　基本的な図形の性質の理解を深め，これを用いるとともに，図形に対する直観力や論証の能力をいっそう伸ばす。
ア　円と直線，二つの円に関する基本的な性質およびこれを用いることならびにこれから類推される球の性質。

イ　円周角と中心角との関係およびその簡単な応用。

※(３)　平衡線，角の二等分線，線分の垂直二等分線，円などが，ある条件を満たす点の動いてできたものとみなすことができること，および点の運動によって，新しい図形が生まれることを理解させる。

※(４)　※(３)の場合にむいて，条件がさらに一つ加われば，点の位置が決定することを理解させる。また，このことを利用して作図ができるようにする。

動心円，用心線，内接，外接，共通内接線，共通外接線，円周角

(１)　Ａにおいて分母を有理化する場合は，ｂ／√ａの有理化の程度とする。

(２)　Ｂ※(２)の式を文字で置き換える場合は，単項式や簡単な二項式を一つの文字で置き換える程度とする。

(３)　Ｃ(２)については，第２学年において扱うことができる。

(４)　Ｃ※(３)における二次三項式のグラフについては，主として点をとってグラフをかくことを扱う。

(５)　Ｅ(１)※ウの作図による方法については，原理を扱う程度とする。

(６)　Ｅ(２)アのうち，円と直線および二つの円に関する基本的な性質の一部を，第２学年において扱うことができる。

(７)　論証の対象としての図形の取り扱いについては，第２学年の３の(３)に準ずる。

(８)　選択教科としての数学は，必修教科としての数学と密接な関連を図って，指導計画を立てて実施するようにする。また，選択教科としての数学と必修教科としての数学とを合わせて一貫した指導計画を立てて実施することもできる。

第３　指導計画作成および学習指導の方針

１　各学年の内容は，五つの領域（数，式，数量関係，計量および図形）に分けて示してあるが，これはこの五つの領域に分けて指導したり，示した順序に指導したりすることを意味するものではない。指導計画を作成する場合には，各領域の中の内容の前後関係や他の領域の中の内容との関連を考え，これらの内容がすべて含まれるよう適切に計画しなければならない。

２　各学年の内容として示したものは，その取り扱いに深浅の程度が考えられるから，実情に即して適切な指導する事項や指導法を考慮する必要がある。

３　概念や原理・法則を理解させる場合には，なるべく多くの具体的なものを与えて，抽象化できるようにするとともに，概念や原理・法則などを実際の場に用いて具体化できるようにすることを考慮する必要がある。また，指導の内容に応じて，実測などの各種の作業も重視して指導することも考慮しなければならない。

４　生徒が与えられた問題を解くことも重要であるが，それとともに進んで問題を見いだし，その解決に努力することも重要である。そのためには，常に生徒の自主的な学習を尊重し，創意くふうする態度を育てるように努めることが必要である。

５　図形や数量における演えき的な考え方の指導については，生従の発達段階をじゅうぶん考慮し，演えき的な考え方を漸進的に向めていくように配慮することが必要である。

６　数量の指導と図形の指導との関連に意を用いて，数学を一体として学習できるようにすることが必要である。

７　数学の学習の素材として，他の教科の学習の成果も用いたり，また，数学の学習の成果を他の教科の学習において用いたりできるように留意する必要がある。

８　生徒の視力またはその他の視機能の障害の状態，失明の時期，生育歴および視覚表象の有無等の違いは，数学科の指導上いろいろと関係するから，これらをじゅうぶん慮することが必要である。