第3節 数 学
第1款 目 標
1 数学における基本的な概念,原埋・法則などを理解させ,より進んだ数学的な考え方や処理のしかたを生み出す能力を伸ばす。
2 数学における基本的な知識の習得と基本的な技能の習熟を図り,それらを的確かつ能率的に活用する能力を伸ばす。
3 数学的な用語や記号を用いることの意義について理解を深め,それらによって,数学的な性質や関係を簡潔,明確に表現したり,思考したりする能力を伸ばす。
4 ものごとを数学的にとらえ,その解決の見通しをつける能力を伸ばすとともに,論理的な思考の必要性を理解し,筋道を立ててものごとを考えていく能力と態度を養う。
5 数学が体系的にできていることと,その体系を組み立てていく考え方を理解させ,その意義を知らせる。
6 数学が生活に役だつことや,数学と科学・技術その他との関係などを知らせ,数学を積極的に活用する態度を養う。
以上の目標の各項目は,相互に密接な関連をもって,全体として「数学」の目標をなすものであり,「数学」の各科目の目標のもととなるものである。指導にあたっては,各科目の目標とともに教科の目標の達成に努めなければならない。
第2款 各 科 目
第1 数 学Ⅰ
1 目 標
(1) 代数における基本的な概念,原理・法則などを理解させ,式を的確かつ能率的に活用する能力を養う。
(2) 初等的な関数について理解を深め,代数的な操作を運用する能力を伸ばす。
(3) 図形の研究における解析的な方法を理解させ,これを用いて図形や数量の関係を適切に表現し,考察する能力を養う。
(4) 平面図形や空間図形についての基本的な概念や性質の理解を深め,これを応用する能力を養う。
2 内 容
以下に示す「数学Ⅰ」の内容は,5単位を標準とし,全日制の課程にあっては第1学年,定時制の課程にあってはこれに相応する学年において履修させることを前提として作成したものである。
(1) 式とその計算
式について,その概念の理解を深めるとともに,計算の基本的な法則を明らかにし,計算する能力を伸ばす。
ア 整式と分数式
(ア) 整式とその計算
主として,乗法・除法とする。また,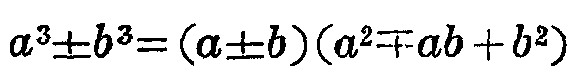 を用いる程度の因数分解を含む。
を用いる程度の因数分解を含む。
(イ) 分数式とその計算
イ 無理式
用語と記号
整式,次数,分数式,有理式,既約分数,無理式,│a|,有理化
(2) 方程式と不等式
方程式と不等式の基本的な概念および性質ならびに解法の原理の理解を深め,これらを活用する能力を伸ばす。
ア 二次方程式
(ア) 根の公式と判別式
(イ) 複素数とその四則
イ いろいろな方程式
(ア) 簡単な分数方程式・無理方程式・高次方程式
二次方程式に帰着できる程度とする。
(イ) 連立方程式
二元二次方程式の程度とする。
ウ 不等式
(ア) 不等式の基木的な性質
(イ) 一次不等式,二次不等式
用語と記号
完全平方式,実数,虚数,虚数単位,i,複素数,実根,虚根,判別式,重根,分数方程式,無理方程式,同値,必要条件,十分条件,恒等式,因数定理,絶対不等式,条件つき不等式
(3) 関数とそのグラフ
関数の概念の理解を深め,初等的な関数について,その関数の特徴を明らかにする。
ア 二次関数,分数関数,無理関数
(ア) 二次関数
グラフの対称性と頂点
(イ) 簡単な分数関数・無理関数
分数関数はy=ax+b/cx+d
’,無理関数はy=√ax+b程度とする。
イ 三角関係
(ア) 一般角の三角関数
(イ) ある角の三角関数と,その角の符号を変えた角,余角および補角の三角関数との関係
(ウ) 弧度法
ウ 指数関数
(ア) 指数の拡脹
(イ) 簡単な底の指数関数
エ 対数関数
(ア) 対数
(イ) 指数関数と対数関数との関係
(ウ) 対数計算,計算尺の原理
用語と記号
関数(函数),f(x),分数関数,無理関数,コタンジェント,cot,一般角,動径,象限,周期,周期関数,正弦曲線,ラジアン,指数関数,底,累乗根,指数法則,対数,真数,対数関数,逆関数,logax,常用対数,logN,指標,仮数
(4) 平面図形と式
平面図形,座標の概念および平面図形と式との関係について理解を深める。
用語と記号
軌跡
(5) 空間図形
空間における直線,平面などの関係およびそのとらえ方について理解を深めるとともに,空間座標を導入し,空間図形の概念を豊かにする。
ア 直線,平面などの関係
(ア) 直線・平面の結合関係・位置関係および二面角
(イ) 三垂線の定理
(ウ) 直線,平面および円の投影図
イ 空間座標
点の座標,二点間の距離(球の方程式にふれる。),座標平面に平行な平面用語と記号
二面角,正射影,跡(直線,平面に関するもの),だ円(長円)
(6) 数学と論証
体系的に論理を進めていく方法を,図形や数・式を通して理解させる。
ア 公理,定理,証明
イ 命題とその逆
ウ 証明の方法
直接証明法,間接証明法
用語と記号
命題,公理,逆,対偶,背理法
3 指導計画作成および指導上の留意事項
(1) 中学校において,選択教科の数学を履修していない生徒に対しては,その内容を適宜補充して指導するように考慮する。
(2) 内容は,六つの領域に分けて示してあるが,これは六つの領域に分けて指導したり,示した順序に指導したりすることを意味するものではない。指導計画を作成する場合には,各領域の中の事項,用語記号の前後関係やこれらと他の領域の中の事項,用語,記号との関連を考えて,適切に計画しなければならない。以下「数学ⅡA」「数学ⅡB」,「数学Ⅱ」および「応用数学」においても同様とする。
(3) 2の(4)のうち,平面図形については,初等幾何学的な扱いを加えて指導してもよい。
(4) 2の(6)数学と論証の内容は,図形と数・式を用いて指導しても,または両者のうちのいずれかを用いて指導してもよい。また,2のうちの(1)から(5)までの指導に際して,適宜のとこで扱ってもよい。
なお,論証の対象としては,基本的で平易なものを取り上げることとし,公理群の無矛盾性や独立性などは扱わないものとする。
(5) 数学的な考えの一つとして,集合の考えを,たとえば不等式と領域,軌跡などのような内容と関連して,指導することが望ましい。また,集合の「含む」,「含まれる」の関係を表わすのに,記号・・を用いてもさしつかえない。
第2 数 学 ⅡA
1 目 標
(1) 基本的な計算法について理解させ,これを用いる能力を伸ばす。
(2) 確率と統計の基本的な概念,法則などを理解させ,これらを用いる能力を養
う。
(3) 数列と極限の基本的な概念,法則などを理解させる。
(4) 微分法と積分法の基本的な概念とその応用について,簡単な整関数の範囲で
理解させる。
2 内 容
「数学ⅡA」は,「数学Ⅰ」を履修させた後に履修させるものとする。以下に示す「数学ⅡA」の内容は,4単位を標準とし,全日制の課程にあっては第2学年および第3学年,定時制の課程にあってはこれに相応する学年において履修させることを前提として作成したものである。
(1) 計 算 法
近似値や誤差について理解を深めるとともに,表・図などによる計算法について理解させ,これらを用いることができるようにする。
用語と記号
絶対誤差,相対誤差,近似式
(2) 確率と統計
確率の概念を明らかにするとともに,記述統計について理解を深める。また,推測統計の基本的な概念を理解させ,統計的な見方や考え方を養う。
ア 確率
(ア) 順列と組合せ
nPrとnCrの程度とする。
(イ) 確率の意味
(ウ) 確率の計算
加法定理,乗法定理
イ 統計
(ア) 標準偏差
(イ) 推測統計の考え方
母集団,標本,標本調査
用語と記号
順列,nPr,組合せ,nCr,階乗,nl,確率,余事象,独立事象,従属事象,排反事象,加法定理,乗法定理,期待値,標準偏差,標本,母集団
(3) 数列と極限
簡単な数列について,自然数との対応関係を考え,その数列の特徴をとらえさせる。また,数列および関数の極限の概念を理解させる。
ア 等差数列,等比数列
年金,償還などを含む。
イ 数列の極限
無限等比級数を含む。
ウ 関数の極限
直観的に扱う。
用語と記号
数列,第n項,一般項,等差数列,公差,Σ,等比数列,公比,極限,lim,→,∞,極限値,収束,発散,無限等比級数,循環小数
(4) 微分法と積分法
微分係数,導関数および積分の概念とこれらの応用について,四次までの整関数の範囲で理解させる。
ア 導関数とその計算
(ア) 微分係数
(イ) 導関数の計算
関数の和・差の導関数
イ 導関数の簡単な応用
接線,関数値の増減,速度,加速度など
ウ 不定積分とその計算
エ 定積分とその簡単な応用
用語と記号
平均変化率,増分⊿x,微分係数,導関数,f'(x),y',dy/dx,極大,極小,極値,不定積分,積分定数,

3 指導計画作成および指導上の留意事項
(1) 「数学ⅡA」の指導にあたっては,学習が平易に進められるよう特に留意し,なるべく実用的な面を多く取り入れるようにするとともに実験・実習を通して学習させるようにする。
第3 数 学 ⅡB
1 目 標
(1) 順列と組合せの基本的な概念,法則などを理解させ,これらを応用する能力を養う。
(2) 数列と級数の基本的な概念,法則などを理解させ,これらを応用する能力を養う。
(3) 三角関数の基本的な概念,法則などの理解を深め,これらを応用する能力を伸ばす。
(4) 図形の研究における解析的な方法の理解を深め,これを用いて図形や数量の関係を適切に表規し,考察する能力を伸ばす。
(5) 微分法と積分法の基本的な概念,法則などを理解させ,簡単な整関数について,それらを用いる能力を養う。
2 内 容
「数学ⅡB」は,「数学Ⅰ」を履修させた後に履修させるものとし,引き統き「数学Ⅲ」を履修させることをたてまえとする。以下に示す「数学ⅡB」の内容は,5単位を標準とし,全日制の課程にあっては第2学年,定時制の課程にあってはこれに相応する学年において履修させることを前提として作成したものである。
(1) 順列と組合せ
具体的な事象において起こりうる場合を分類,整理し,場合の数を数えやすくする方法を明らかにする。また,これに関連して,二項定理を理解させる。
ア 場合の数の数え方
イ 順列と組合せ
重複順列と重複組合せは,これらの考え方にふれる程度とする。
ウ 二項定理
用語と記号
順列,nPr,組合せ,nCr,階乗,nl,二項定理
(2) 数列と級数
簡単な数列について,自然数との対応関係を考え,その数列の特徴をとらえさせる。また,数列について,極限の概念を理解させる。
(3) 三角関数とベクトル
正弦定理,余弦定埋および加法定理を理解させ,これらを応用する能力を養う。また,ベクトルの概念を理解させる。
ア 三角形への応用
正弦定理・余弦定理,三角形の面積
イ 加法定理
複素数の極形式(z=r(cosθ+isinθ))を含む。
ウ ベクトル
(ア) べクトルの意味
(イ) 加法,減法,実数との乗法,内積
用語と記号
正弦定理,余弦定理,加法定理,複素平面,絶対値(複索数に関するもの),偏角,ベクトル,成分,内積
(4) 図形と座標
図形の解析的な研究方法を用いる能力を伸ばすとともに,座標変換の考え,極座標などを導入し,座標の概念の理解を深める。
用語と記号
焦点,準線(放物線に関するもの),長軸,短軸 直角双曲線,漸近線,二次曲線,媒介変数,極座標,直交座標
(5) 微 分 法
微分係数や導関数の概念を理解させ,簡単な整関数の範囲で,導関数を計算したり,それを応用したりする能力を養う。
ア 微分係数
イ 導関数とその計算
関数の和・差・積の導関数
ウ 導関数の応用
接線,関数値の増減,速度など
用語と記号
区間,平均変化率,増分,⊿x,微分係数,導関数,f'(x),y’
,dy/dx,極大,極小,極値
(6) 積 分 法
不定積分や定積分の概念を理解させ,簡単な整関数の範囲で,積分を計算したり,それを応用したりする能力を養う。
ア 積分の意味
イ 積分の計算
ウ 積分の応用
面積,体積,道のりなど
用語と記号
不定積分,積分定数,

3 指導計画作成および指導上の留意事項
第4 数 学 Ⅲ
1 目 標
2 内 容
「数学Ⅲ」は,「数学ⅡB」を履修させた後に履修させるものとする。以下に示す「数学Ⅲ」の内容は,5単位を標準とし,全日制の課程にあっては第3学年,定時制の課程にあってはこれに相応する学年において履修させることを前提として作成したものである。
(1) 微分法とその応用
微分法について理解を深め,簡単な有理関数,無理関数,三角関数,指数関数および対数関数の範囲で,導関数を計算したり,それを応用したりする能力を伸ばす。
ア 関数の極限
直観的に扱う。
イ 導関数とその計算
(ア) 関数の商および合成関数の導関数
(イ) いろいろな関数の導関数
(ウ) 第二次導関数
(エ) 平均値の定理
直観的に扱う。
ウ 導関数の応用
(ア) 接線,関数値の増減,曲線のおうとつ,加速度など
(イ) 近似式
用語と記号
第二次導関数,y",f"(x),d2y/dx2,変曲点,近似式,自然対数,e
(2) 積分法とその応用
積分法について理解を深め,簡単な有理関数,無理関数,三角関数,指数関数および対数関数の範囲で,積分を計算したり,それを応用したりする能力を伸ばす。
用語と記号
置換積分,部分積分,微分方程式
(3) 確率と統計
確率の概念を明らかにするとともに,確率の考えを用いて,統計に対する見方や考え方を深める。
3 指導計画作成および指導上の留意事項
第5 応用数学
1 目 標
職業に関する専門教育で必要とする数学的な概念およびこの概念とそれが応用される事象との関連を理解させ,数学的に処理する能力を養う。
2 内 容
「応用数学」は,原則として,「数学Ⅰ」を履修させた後に履修させるものとする。以下に示す「応用数学」の内容は,職業教育を主とする学科において,その必要に応じて,その中から適切な事項を取り出して履修させることを前提として作成したものである。
(1) 三角関数
(2) 計 算 法
ア 補間法と実験式
イ 近似値と誤差
近似値の計算,簡単な近似式
ウ 図による計算
エ 複利計算(年金,償還などを含む。)
オ 計算機器
(3) 図形と方程式
ア 二次曲線
標準形の方程式,接線の方程式
イ 曲線の表わし方
媒介変数および極座標による表わし方
ウ 空間図形
平面および直線の方程式,二次曲面の標準形の方程式
エ べクトル
加法,減法,実数との乗法,内積,外積
(4) 数列と級数
ア 等差数列,等比数列
イ その他の数列
一般項がn2,n3の程度とする。
ウ 無限等比級数
(5) 微 分 法
(6) 積 分 法
ア 不定積分と定積分
イ 積分の計算(簡単な置換積分・部分積分を含む。)
簡単な初等的な関数の範囲で扱う。
ウ 積分の応用
(ア) 面積,体積,道のりなど
(イ) 物理などへの応用
(ウ) 定積分の近似計算
(エ) 簡単な微分方程式
axd2y/dx2+bxdy/dx+cy=0の程度とする。
(7) 確率と統計
ア 順列,組合せ,二項定理
イ 確率,確率の計算,期待値
ウ 記述統計
偏差,相関
エ 二項分布,正規分布
オ 標本調査
抽出,推定,検定
〔備考〕
学科によって必要があれば,たとえば,次のような事項を指導してもよい。
行列式
画法幾何
球面三角法
ラプラス変換
3 指導計画作成および指導上の留意事項
(1) 「応用数学」の標準単位数は6単位であるが,この場合でも,2に示した内容の全部を取り上げることを意味するものではない。したがって,学科によって,それぞれの必要に応じて,この内容の中から適切な事項を取り上げて計画し,指導することが必要である。
(2) 指導計画を作成し,指導するにあたって,学科に応じて,内容の中の事項を取り上げる場合には,「数学」の目標と「応用数学」の目標を考慮するとともに,下記の事項に留意する必要がある。
ア 職業に関する専門教育の学習に用いられる数学的な内容の中でも,基本的で発展性があり,広く,よく用いられるものであること。
イ 取り扱う内容の数学的な意味や応用のしかたなどについて,生徒が理解できる程度のものであること。
ウ 取り扱う内容によっては,そこで取り上げる定理や法則の意味やその応用のしかたなどに指導の重点をおき,必ずしも厳密な論理によって展開する必要はないこと。
(3) 用語と記号については,おおむね「数学ⅡA」,「数学ⅡB」および「数学Ⅲ」の内容に示した用語と記号に準じて,適宜指導するものとする。
![]() を用いる程度の因数分解を含む。
を用いる程度の因数分解を含む。