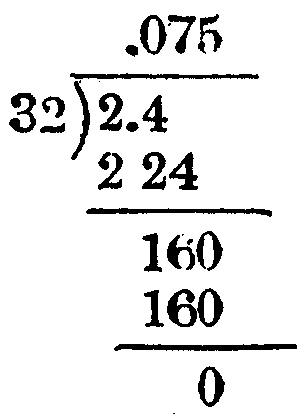第Ⅶ章 数学科の学習指導における評価
§1.数学科の学習指導における評価のねらい
学習指導において,評価ということが,きわめて重要なことであると考えられている。しかし,「評価とはどんなことであるか」また,「なぜ,評価が重要であるか」という問題については,人によって,いろいろ違った考えが持たれているようである。
たとえば,評価をすることを,単にテストしたり,指導要録に書き入れたりすることであると考えている人がある。しかし,評価ということが,単に,そのようなことをするだけで終ってしまうものであるとしたら,その価値は大して大きなものであるとはいえないであろう。
学習指導においては,テストや指導要録から得られる資料を,教場での実際の指導に結びつけ,学習指導をより有効にしていくことができてこそ,テストをしたり,指導要録に記入したりすることが,意味があることになる。いいかえれば,テストをしたり指導要録をつけたりすることは重要なことであるが,それだけで評価が終るのではなく,いわば,それらが,学習指導をよりよくしていくために有効な資料を提供し,学習指導の上に何かがプラスされてはじめて,評価が達成されるということができよう。
さらに,この評価は,テストや指導要録によるだけでなく,もっと広い立場からの教師のはたらきによることが必要であると考えられる。これを,日常,人に話をするときのことを例にとって,明らかにしてみよう。
人に話をするとき,相手がどんな人であるかがよくわかっていて,前もって,どんなことを,どんなふうに話したら,話がよくわかるかを考えておくと,そうしないときよりも,人に話をいっそうよくわからせることができるし,自分のほうでも,話しやすいものである。また,いったん話そうと計画したことも,実際に話をするとき,そのまま一方的に話をするよりも,その人の顔つきや態度などに注意しながら,それに応じて,自分の話そうとしたことの内容や話し方などを,適当にかえていくようにしたほうが,いっそう相手にわかりよいものである。
さらに,相手が,自分でわからない点を質問してくれたり,その人の好きな点やよくわかっている点をいってくれたりすると,それに合ったように話をしやすいから,いっそう相手にわかりよくすることができるし,話を能率的に進めることもできる。
このように,人に話をわかりよくすることができるのは,次の事がらによると考えられる。まず,前もって,相手の人の状況を調べること,さらに,その場に臨んで,その人の表情を絶えず観察することや適当な質問を出したり受けたりすることなどである。このような事がらをとおして,相手の実際の理解の程度や気持にさぐりを入れ,自分の話そうとすることを,よりよくわからせたり,話し方をくふうしたりするための目安をよくつかむことができるからである。すなわち,このような場合,相手が変な顔付きをしたとか,態度がよくなかったというようなことは,だれでも気の付くことではあるが,それを単にそれだけにとどめないで,自分の話し方とくふうするために生かすことが,人にわかりよく話すのに役だつのである。
生徒の学習を指導する場合の評価についても,これと同じことがあてはまるわけである。生徒に,たとえば,移項の考えを用いて,方程式を解くことを指導しようとするときについて,考えてみよう。この指導をするにあたっては,まず生徒が,等式の性質がよくわかっていなければならない。また,移項の考えが有用であることがわかる程度に,方程式が解けるようになっていなければならない。これらの基礎的な理解や能力が,実際にどんなであるかが教師によくわかっていないと,移頃の考えを指導しようとしても,効果をあげることができない。
また,これらの基礎的な理解や能力がじゅうぶんであるとみられたので指導にはいったとする。そのときでも実際は,何か予期しない困難にぶつかることがある。たとえば,xの係数が1であると考えることができなくて,困っているようなことが起る。このような困難は,その指導の中で,臨機に除去していくことが必要である。それゆえ,実際の指導にはいっているときでも,生徒の学習の態度や感情をよく観察して,何かつごうの悪いことが起っているとわかったら,あるいは,そのような悪い結果を起しそうな微候を見いだしたら,初めの計画を修正して,その場合を避けるようにするとか,または,いくらかの時間を割いて,その理解にあててかかるとかなどしてやると,指導の効果を,より大きくすることができる。さらに,このとき,生徒自身が,どこが困難かを研究できるように,目安を与えるようにすると,いっそうつごうがよい。
この例でわかるように,学習指導の場合にも,教師は,指導の効果をあげるために,指導の計画をたてたり,指導の方法をくふうしたりするのに役だつように,相手とする生徒たちが,実際に,どんなであるかを,あらゆる機会や方法によって,とらえていくことが必要である。このことから,学習指導における評価とは,上のような教師の働きをとおして,その教師が学習指導の上に,なんらかの改善を行っていくことであるということができる。学習指導において評価が重要であるといわれるのは,このような改善を常に行っていくことが必要であることにほかならないのである。
評価についての,以上のような考え方から,学習指導における評価のねらいを大きくまとめてみると,次の二つを考えることができる。
このような事がらは,教師も,生徒も,いつも行おうと努力していることである。しかし,教師の指導の相手は,生きた生徒であるから,いっそうこのことに注意して,指導上の大きな誤りを未然に防ぐようにし,生徒にむだな時間を費さしたり,誤った方向へ導いたりしないようにすることが必要である。
| 教師の学習指導を,生徒の実際によく合うようにするにはどんなことをねらって評価したらよいか |
学習指導を生徒の実際に合うようにするとは,たとえば,指導計画をたてるのに,単に,他の学級と進度をそろえる目的から指導内容を決めたり,教科書ではその順番になっているからというだけのことで,それをとりあげたりしないことである。また,同じく生徒の能力を考えて計画をたてるとしても,以前の一つのテストの結果に基いてするよりも,毎時の学習指導で,よく調べた事がらによるようにすることであるといえる。
それでは,この生徒の実際に合うようにすることをねらって評価するのに,どんなことが考えられるか。これは,指導の計画をたてる場合にも,実際の指導をする場合にも重要なことであるから,この二つの場合に分けて,説明してみることにする。
1.指導の計画を,生徒の実際に合うようにするには,どんなことをねらって評価したらよいか。
これには,次の二つの観点が考えられる。
(a) 生徒にとっては,どんなことの指導が必要であるか。
(b) 生徒は,どれだけのことがやれそうか。
これを,さらに具体的にいってみると,次のようなことが考えられる。
○個々の生徒にとって,得意なところと,不得意なところとをみる。
前者は,いっそう伸ばすようにし,後者は,うまく補っていくように,指導計画の上でくふうをする。
○生徒が,現在,どんな数学的な理解や能力がよくできなくて,困っているかをみる。
その困難を解決するのに役だつ経験をとりあげたり,そのための機会が与えられるように,指導計画の上でくふうをする。
○生徒が,これまでにどんなことを学習してきたかを調べる。
これに基いて,生徒たちが,数学的な経験をうまく積み重ねていくことができるように,指導計画のくふうをする。
○指導の目標としたことが,生徒たちが努力すればやれそうなものかどうかをみる。
無理がありそうであったり,あまり程度が低くすぎるとみられるものであったりする場合には,それを適当に加減して,個々の生徒の能力に合うようにする。
○とりあげる問題が,生徒の個人的な能力の差異に応ずるだけの幅があるかどうかをみる。
学習の進んだ生徒も,遅れている生徒も,それぞれの能力の範囲で解決できるような問題を,できるだけとりいれるようにくふうする。
これらは,特に重要であるとみられるものをとりあげたものである。これを,さらに,一つの例について,説明してみる。
〔例〕 中学一年で,食事についての単元を指導しているとき,百分率の意味と,百分率の一段の用法を指導したあとで,これらについて,どの程度理解できているかを知って,次の二段の用法に進んでよいかどうかをみるために,次のテストを用いた。
(テストの問題)食品甲・乙・丙および丁には,それぞれ,次の割合でたんぱく質が含まれている。たんぱく質の含まれている割合は,それぞれの食品について何パーセントであるか。
(Aの生徒)計算も何もしないで,次のように答えた。
(Bの生徒)次のように式をかいて,答を出した。
甲…20g÷100g=.2 から2%
乙…18g÷100g=.18 から.18%
丙…38g÷200g=.19 から.19%
丁…24g÷150g=.16 から.16%
(Cの生徒)
甲,乙については,計算をしないで,それそれ,20%,18%と答えた。
丙については,38g÷2=19gと計算して,19%と答えた。
丁については,答えてない。
以上3人の答をもとにして,初めの目的に照して考えてみる。
(Aについて)……食品丙および丁についての百分率は,100gについてのたんぱく質の量と見まちがえたものか,あるいは,形式的に,右側の数字にそのまま%をつけ加えて書いたものかどうかは,これだけではわからない。しかし,割合についての今までの様子から考えると,後者の場合にあたるとみて,まちがいないようである。(今までの日常の観察や記録などの資料を,ここで用いる)
これから,A生徒は,百分率の概念の基礎になっている割合の概念が,やはり,まだわかっていないとみられる。したがって,割合の概念が問題となるような具体的な経験をもっと豊富に与えるように,それから確かにしてかかるよう,計画をたてておくようにする。
(Bについて)百分率についての約束,すなわち,全体を100としたときの割合であることがよく理解されていないとみられる。これにさえ注意してやれば,二段の用法へも進めると思われる。したがって,まず,二段の用法へ進むにあたって,上に述べた理解を確かにしてかかるように,計画をたてるようにする。
(Cについて)百分率の意味については,一応理解されているとみられる。しかし,丁食品についての百分率が求められなかったのは,日常の学習からみて,予期に反している。これは,おそらく丙食品についてのやり方からみて24g÷150gとして,割合を小数で表わしてかかることをしないで,24g÷1.5とするような考え方をとったために,まだ学習してない,小数で割るという困難にぶつかったためと考えられる。
それゆえ,丙・丁食品のような場合には,38/200×100,24/150×100,の考え方を用いていけば,小数で割ることをしなくとも,百分率が求められることを理解させておく必要がある。これを理解させれば,次の二段の段階へ進んでよいと考えられる。
この例は,主として,次の目標とすることが生徒にできそうかどうかをみるときについてのものである。要するに,実際の指導にあたっては,できるだけ小修正ですむようにしておくことが重要である。
2.実際の指導を,生徒の実際に合うようにするには,どんなことをねらって評価すればよいか。
指導計画を生徒の実際に合うようにたてておいたつもりでも,実際に指導してみると,必ずしもうまくいかない場合があるものである。また,指導計画がうまくできていても,それにしたがって学習指導がうまく行われるためには,絶えず評価をして,生徒の実際を見ていくことが必要であることは初めに述べたとおりである。
このような評価をするときに,次の二つの観点が考えられる。
(a) 生徒は,学習の目標をよくつかんで,学習をしているか。
(b) 学習の様子に,何か注意すべき事がらが起っていないか。
これを,具体的な事がらにしてみると,次のようなことが考えられる。
○生徒たちは,どんなことがわかって,どんなことがわからないかをみる。
これをもとにして,自分が,どんなことについて学習しようとしているかを,生徒にとって,さらにわかりやすいようにしてやる。
○生徒のやろうとしていることが,どんなことであるかをみる。
これでわかったことをもとにして,生徒のやろうとしていることと,教師が指導しようとしていることが,ちぐはぐでないようにする。
○各生徒の学習が,全体の解決する方向に向いているかどうかをみる。
この状況によって,全体の問題と,各人の学習とのつながりがわかりやすくなるように,指導上のくふうをする。
○生徒が,現在,何か困難にぶつかっていないか,また,それは,どんなことかをみる。
これによって,その困難にうちかつ目安を明らかにしてやったり,無理であると思われるものについては,段階を細かく分けたり,簡単な場合に変えたりなどして,学習がやさしくなるようにしてやる。
○生徒は,何か誤ったことをしていないか,たとえば,用語を正しく理解して使っているかどうか,計算や測定などの技能を正しく使えるようになっているかどうかなどをみる。
このような事がらが見いだされたときには,その原因をよく探って,生徒が,それに気がつき,すぐに直すことができるようのに,取り計ってやる。
これらは,どれも重要と思われる二,三の例にすぎない。これを,さらに具体的な例で説明してみる。
〔例〕 生徒たちが,等式の性質はよく理解しており,次のような方程式を,両辺から同じ数を引いたり加えたり,あるいは,両辺に同じ数をかけたり,同じ数で割ったりして,一応解けるようになっていることが,教師はわかったとする。
3x=x+5
そこで,次の指導目標を考えたとする。
(指導目標)移項の考えを用いると,方程式を簡単に解くことができることを理解させる。
すなわち,上の式で,両辺からxを引いた結果の式は,もとの式の右辺にあるxについて,その符号を変えて,左辺に移したものとみられる。このようにして,両辺に同じ数を加えたり引いたりする手数を省いて,一つの項の符号を変えて移しさえすればよいことが,ほかの方程式の場合にも,常にいえることを理解させる。
(評価) これを実際に指導するのに,上の方程式について,移項の意味を説明し,ほかのいくつかの方程式について,それを調べさせた。このときの状況を観察していると,必ずしも,この学習の目標がよくつかまれているとはみられないものがある。たとえば,次のA,Bのような生徒がいることかわかった。
(A生徒)方程式を解いて,答えを出すことだけにいっしょうけんめいになっており,項の符号のことについては,少しも注意しているようにみられない。
(B生徒)比べようとする項の下に線を引いて,符号に目をつけているように見える。しかし,なんのために項の符号に注意するのか考えないで,ただ,形式的に,ほかの生徒のやっているのをまねているようである。
これをもとにして,次のように考える。
(A生徒の場合)この生徒は,(1)方程式を解くために,等式の性質を用いるだけがせいいっぱいで,移項の考えを用いるだけの余裕がないのか,(2)今までのやり方でよいと思っていて,移項の考えに興味がないのか,あるいは,(3)教師の説明を,たまたま聞きもらしたのでそのようなことをしているのかなどと,一応考えられる。
しかし,日常の能力からみて,移項の考えを用いるだけになっていると考えられるし,ときどき,教師のいうことを聞きもらしたりする傾向があることがわかっているので,(3)の場合であろうと考える。そこで,今,みんなかやっていることを注意してやって,無駄な時間を費さないようにしてやる。
(B生徒の場合)この生徒が,ほんとうに自分でやっているのであるとすれば,今までのテストの結果などを考え合わせて,ちょっと予想外である。そこで,方程式を解いている様子にもっと注意してみて,だれかのまねをしているのかどうかを確かめる。その結果,意味がわからずに,単にまねているのであることかわかれば,方程式を自分で解けるようになるよう努力させるようにして,むだなことをしないように注意してやる。
目標をよくつかんでいないとみられる生徒があることがわかった場合に,それがどんなことに基くかは,表面的な行為の上からだけではわからないことが多い。それゆえ,その生徒のやっていることをいろいろな点から観察したり,あるいは,今までの傾向を参考にしたりして,できるだけ早くその原因を探り出して,有意義な学習ができるようにしてやることが重要である。
| 生徒が自己評価をし,自主的に学習を進めるようにするには教師が評価をするとき,どんなことをねらったらよいか。 |
これまでに述べた評価は,教師が,自分の行っている学習指導を反省して,その学習指導が,生徒の実際に合うように改善していくことをねらっているものである。いわば,教師が,指導という側から,自己評価をしていくことであるといえる。
これに対して,生徒の側でも,進んで学習の目標をつかんだり,学習の成果を知ったりして,自己の学習効果がいっそうよくあがるように反省して,学習を改善していくように努力することが望ましい。これは,生徒が,学習をしているものの立場から,自己評価をしていくようにすることであるといえる。
さて,この生徒の行う自己評価は,教師が自己の指導を評価しようとして,生徒に働きかける過程を通じて,促進されると考えられる。
たとえば,ある生徒が,方程式を解けなくて困っているとする。そこで,教師が,その生徒は方程式についてどんなことがわからないために解けないのかを診断するために,「方程式を解くということは,どんな値を求めることであるか」とか,「未知数の係数をなくするのに,どんな数をかけたらよいか」などを質問したり,あるいは,テストを用いたりして,調べていけば,それと同時に,その生徒も,自分の困難がどんなことにあったかを,それによって明らかにしていくことができるであろう。
また,さきに,評価の観点として,生徒が学習の目標をよくつかんでいるかどうかをみて,目標をつかみやすくすることを考えたことは,とりもなおさず,この生徒の自己評価を援助していることにもなっている。
この教師の評価を通じて,生徒の自己評価を援助するときの観点としては大きく分けて,次の二つのことが考えられる。
1. 生徒が,学習の目標をよくつかめるように,学習の目標をわかりよくするための資料を与えたり,それを生徒が自分でも調べたりする機会を与えたりしていく。
2. 自主的な学習として,望ましい態度が現れているかどうかをみて,それを促進するようにしていく。
このためには,たとえば,次のことがわかるように,教師が調べてそれを生徒に知らせたり,生徒が自分でそれらのことを調べたりするようにする。さらに,その結果を,どんなグラフや表を用いて表わすとつごうがよいか,などについても援助してやるとよい。
○自分がどれだけ学習したか。また,どんな点に改善の余地があるか。
○自分が,現在,どんな理解や能力がよくできなくて,困っているか。
○学習の過程を通じて,特に,(問題解決の過程を通じて)自分が,わかったこと,わからなかったこと。
○自分の能力が,どんな段階にあるか。
○とりあげようとする問題が,解決の見込があるかどうかの見とおし。
○………
次に,自己評価は,学習の成果をあげるために必要なものであるが,これはまた,数学科の一般目標として,望ましい自主的な態度をつちかうもとになるものであると考えられる。望ましい自主的な学習態度が現れやすいような機会を与えたり,生徒にも,その必要がわかるようにしむけたりすることがたいせつである。
このときにとりあげる,望ましい態度をみる観点としては,次のようなものをあげることができる。
○目標を,絶えずよくつかむように学習を進めているかどうか。
○解決すべきことや,その理由を考えてから,解決の方法を問題にしているかどうか。
○問題を分析し,その分析された問題を解決すると,もとの問題が解決されることになるかどうかを反省しながら,やっているかどうか。
○自分でやった事がらに対して,自分で反省し,それに責任をもっていくような傾向があるかどうか。
○失敗した事がらについても,その原因を明らかにして,次に生かしていくように努めているかどうか。
1.評価は指導の一面であること。
教師が,指導をうまくしようと心がけるとき,必然に,その中に評価がはいってくるのであって,評価は,指導と切り離して考えられるものではない。上に述べた例でわかるように,評価のねらいは,第Ⅰ,Ⅱ章でとりあげた,指導上の原則を推し進めることと一致していると考えられるものである。
2.評価では,教師あるいは生徒が,それぞれ,指導や学習の反省をする資料ととして,生徒の理解や能力などを診断的にみることが望ましいこと。
評価は,指導を,生徒の実際に合うようにするのが大きなねらいであるから,生徒についての実際をよく知ることが先決問題である。したがって,生徒の行為を観察したり,理解や能力などをテストなどによって測ったりすることが,評価では,重要な操作である。従来は,このような資料を得さえすれば,それが評価であるとか,それをもとにして,生徒の品等づけをすることが評価であるとか,考えられるような傾向があった。しかし,ここであげたように評価のねらいを考えると,教師も,生徒も,自分の行為を反省し,それを改善していくための資料として,それらを用いてはじめて,意味があるといえる。
また,生徒の能力をみるにしても,さきに述べた例でもわかるように,比の三段の用法を指導したとき,ある生徒が,テストの結果,まだ比の三段の計算ができていないことがわかったというだけでは,指導に役だつとはいえないのである。比の三段の計算ができないのは,B×p=Aという関係についての理解がよくできていないからであるとか,その関係はわかっていても,具体的な場合に,どれがAにあたるか,Bにあたるかを見いだすことができないからであるかなど,それをなおすために必要な原因とみられる事がらがわかるようにみることが必要である。すなわち,できるだけ診断的にみて,次にすべき処置が,ひとりでに出てくるようになっていることが望ましいといえる。これは,生徒の点をつけるための考査などと,大いに異なっている点である。
3.評価は,指導しようとする事がらのすべてについてすること。
評価は,指導を改善することがねらいであるから,指導しようとすることがらすべてについて行われることが必要である。しかるに,指導しようとする目標の中には,それが,うまくいっているかどうかがすぐわかるものもあるが,そうでないものもある。たとえば,目標をよくつかんでやっているかどうか,数学のよさがよくわかっているかどうかなどは,一つの外見上の行為だけからは,なかなかわかりにくいものである。このようなものも,よくとらえるようにして,少しでも,よい学習指導ができるようにすることがたいせつである。
§2.評価の手順と方法
前節で述べたように,学習指導における評価は,学習指導の改善を目ざして,指導と表裏一体となって行われる働きであって,指導と切り離した過程ではないと考えられる。したがって,学習指導が行われているときは,前節にあげたような事がらをねらって,絶えず,評価が行われていることが必要である。
しかし,この学習指導は,多数の生きた生徒を相手とするものであり,力動的に移り進む過程であるから,評価を,うまく行うには,深い観察や臨機応変の判断が必要である。
そこで,評価が熟練した少数の教師だけでなく,生徒の学習指導にあずかるかぎり,どの教師にもできて,しかも,大きな手落ちのないようにするために,何か手順や方法を考えておくことが,必要となる。この手順や方法を,できるだけ主要な焦点に対して評価のための注意が集中できるようにしていくという観点で,考えてみることにする。
たとえば,方程式について指導しているときでも,評価としては,生徒がその指導に関係があるとみられる行為とすれば,どれもとりあげていかなければならない。しかし,その時間には,主として移項の考えを指導することになっているとすれば,それに関する生徒の学習について,どんな行為が起るかを,あらかじめよく考えておけば,それだけ実際に臨んで気楽になるし,それに関して,手落ちもなくなるものである。また,この移項の考えがよく理解されたかどうかは,普通に学習指導をしながらも,いつもみていくのであるが,特に,次の段階に進むときなどに気をつけて,手ぬかりのないように評価すれば,それ以外のときには,評価に対して,少しは気を抜いていても,大きな手落ちがなくなる。また,全部の生徒について,同時に学習の成果を知る必要があるとき,適当なテストなどを準備しておいて,それを利用すると,一時に皆のものについて調べることの気苦労を避けることができて,つごうがよい。
このような考えから,評価を,手ぎわよく,できるだけ能率的にやるための方法として,次の四つの事がらをあげることができる。
Ⅰ.どんな事がらで評価するかを,はっきりとつかんでおく。(目標のはあく)
Ⅱ.どんな機会に評価するのが有効かを,考えておく(時間の選定)
Ⅲ.適切な評価の用具を選んで,準備しておく。(用具の選定)
Ⅳ.評価で得られる資料を,適切に記録していく。(資料の記録)
計画的に評価をしていこうとするとき,この手順をふんでいくことは,評価を手落ちなくする上によいことである。しかし,前もって,評価の計画を考えておくことのできない臨機の事がらに対しても,評価をすることがたいせつである。この手順は,いわば,そのような臨機の評価のために,より多くの労力をまわせるようにするために,計画的な評価を手ぎわよくするためのものであるといえる。以下,これらの手順について,具体的に説明をすることにする。
Ⅰ.目標のはあく
まず,どんな事がらに基いて評価するかを,考えておくことが必要である。一つの目標について指導しているときでも,生徒がみな同じような行為をするとは限らないで,いろいろな生徒の行為が現れてくる。
たとえば,方程式を,移項の考えを用いて解けるようになることを指導目標としているときには,生徒の中には,必ず,次のような行為をするものが出るであろう。すなわち,移項の考えがもうすでによくわかったものは,いちいち両辺に同じ数を加えたり引いたりしないで,方程式を手軽に解いていくだろう。また,まだ移項の考えがよくわからないものは,あいかわらず,もとのまわりくどいやり方を用いて方程式を解いているであろう。
ところが,この場合にみられる生徒の行為としては,数学的なことだけについていっても,これだけではないのが普通である。たとえば,すでにわかっているはずの等号の意味の理解がまだあいまいで,誤った使い方をするものがあったり,あるいは,たまたま係数が小数や分数であるために,その係数の乗除ができなくて困っていたりするものもある。
これらの行為は,計画の上では,あらかじめ,予想されていない事がらであっても,学習指導の能率をあげるためには,どれも,なんらかの形で,とりあげなければならない事がらである。
このように,いろいろな行為が起っても当惑せず,ある行為は,今指導していることについて,どの程度の理解を示しているものか,また,ある行為は今救ってやらなければならないものかなどを判断することが必要である。
このように評価ができるためには,次のようにしておくことが必要である。
1.どんな数学的目標をねらっていくかを,分析して,それをはっきりと決めてかかる。
このことは,生徒が予期しない行為を示した場合に,それをその場でとりあげるのが適当かどうかを判断するのに重要である。
たとえば,方程式を指導する場合でも,実際には,次のように,いろいろの段階があるわけである。
(a) 公式をもとにして未知の文字の値を求める程度で,方程式ということばを指導する。
(b) 等式の性質をもとにすれば,どんな形の一次方程式でも解けることを指導する。
(c) 移項の考えを用いて,手軽に解くことを指導する。
(d) 方程式をできるだけ速く解くための練習をさせ,その練習をとおして不確実な点を見いだして指導する。
そこで,ばく然と方程式を指導するというのではなく,このうちの,どれを主としてねらっているのかをつかんでおくと,次のような点でつごうがよい。
上記の(c)の段階の指導をねらっているときに,等号の意味がわからないような生徒を発見したとする。等号の意味の理解は,方程式を解くときの基礎的なことであるから,これは,方程式にはいる前にとりあげて,正しく使えるようにしてやらなければならない。しかし,分数・小数の乗除で困っている者を発見したときは,そこで,その生徒に,分数・小数の乗除を指導することはわき道にはいりすぎると考えられるから,分数や小数が係数に現れないものだけを取り扱うようにして,その生徒が移項の考えの理解に集中できるようにしてやる。そして,分数・小数の乗除についての補習は,(d)の段階の指導のときにゆずることにする。このようにして,指導の範囲を限定し,複雑にならないようにして,指導能率をあげるようにする。
このように評価ができるためには,上にあげたように,指導の目標がはっきりつかまれていることが前提となるのである。
2.どんな行為が起るかを予想して,具体的な事例でつかんでおく。
実際の学習指導の場において,多種多様の生徒の行為が現れた場合でも,これらの行為の多くが予期されているときには,それだけ当惑することが少なくて指導がうまくいく。
生徒の行為を予想する場合にたいせつなことは,それを具体的な事例でつかんでおくことである。それは,生徒がある行為をしたら,すぐに,それが予想したものに該当するかどうかを容易に見分けることができるようにするためである。
たとえば,「移項の考えをうまく使って方程式を解く」といっても,どんなことをさしているかがわかっていなければ,役にたたない指導する教師にとって,今までの経験からみて,「ああ,あのような場合に生徒がこんなにすることだな」というように,具体的な事例が浮んでいることが必要である。
また,この移項の指導にあたって,等号の意味がよくわからない生徒があるかもしれないと予想していても,抽象的な分析だけではすぐに役だたない。たとえば,等式の意味がわからないとは,方程式の変形をするとき,
としたりするようなことであるなどと,はっきりしていると,等式の意味のわかっていない生徒を,容易に見つけ出すことができることになる。
ここで,単に具体的な事例がわかっているだけでなく,それはどんなことがもとになっていることかもわかっていることも重要なのである。ことばをかえていえば,現れる行為とそのもとになっているものとの対応がよくできていることが必要である。すなわち,これこれの行為が現れたら,こんなことがまだよくわかっていないはずだとか,こんな誤りに落ちこむ徴候だというようなことがわかっていることである。
もちろん,実際に,このような対応を考えるにあたっては,ただ一つの行為から,すぐに結論はこうこうだということは危険なことである。その前後の行為との関係なども,よくとらえて考えていかなければならない。また,個々の生徒についてのいろいろな事例をとらえ,それを,継続的に調べておくことや,多数の生徒についての事例から,帰納的に研究しておくことも必要である。
このようにして,目標をはっきりとつかんでおくと,しだいに,評価を手ぎわよくすることができるようになる。このために,目標などについて概念的に分析をすることもたいせつであるが,それとともに,今までの経験をとおして,具体的な事例をもとにした研究を積んでおくことも,忘れてはならない。
Ⅱ.時期の選定
学習指導においては,絶えず,生徒の行為に注視して,評価していくことがたいせつである。しかし,適当な機会をとらえて,その際に,特に気をつけて評価するようにしても,主要な学習の成果については,大きな見落しをすることなく,手軽に評価していくことができると考えられる。
この評価の機会を考える場合に,次のようなことを考慮するとつごうがよい。
1.一度に,多くの指導目標が重ならないようにすること
実際の学習指導にあたって,一度に多くの指導目標をねらっていると,評価があいまいとなり,また,困乱もしやすい。
この意味で,指導目標をうまく整理して,できるだけ,一つ一つの指導目標を次々にねらっていくようにし,その一つごとに評価の機会を設けていくことができることが望ましい。すなわち,学習指導の適当なところどころにくぎりをいれて,そのくぎりごとに指導したことについて,いわば,まとめをしていく。しかも,このくぎりの中では,指導目標としてねらうことは,できるだけ一つになっているとつごうがよい。
このようにくぎりを考えておくことは,指導計画を評価する一つの目安にもなる。すなわち,学習指導では指導のくぎりごとに,必ず,何か数学科として指導すべき事がらが含まれているかどうかを調べて,指導することにむだのある授業が行われることのないようにするのに役だてることができる。
2.診断が単純にできるように,理解の段階ごとに評価すること
生徒が期待した成果を示さなかったり,何か困難にぶつかったりしていたとき,それはどんなことがわからないのがその原因になっているかということが,はっきりわかって,治療の目安をたてることができることが,評価の大きなねらいである。
ところが,数学の学習においては,わからないでいる生徒を見つけたとしても,治療するのに,どこから手をつけて指導したらよいか,見当のつかないような場合がある。これは,生徒にわからないことがいくつも重なってしまうまで評価しないで放っておいたことが原因になっていることが多い。そこで,1.で述べたように指導にくぎりをつけるときは,指導目標に新しいことが加わるごとに,くぎることにし,指導することがいくつも重ならないうちに,必ず評価できるようにすることが必要である。
たとえば,方程式を解くことを指導する場合について考えてみよう。
まず,
などの一段階で解ける方程式について,等式の性質(両辺に同じ数を加減しても,また,両辺を同じ数で乗除しても等式がなりたつこと)を理解させながら,方程式を解くということの意味を指導する。
のような方程式について,方程式を解くためには,まず,未知数が左辺に,既知数が右辺にくるように,適当な未知数や既知数を両辺に加減してかかればよいということを理解させるとする。
以上の指導で,初めの段階で,2x=8やx+3=5の型の方程式が解けるかどうかについて評価して,それが必ずできることを確めておいてから,次の段階に移れば,4x−5=2x+1の型の方程式ができないときは,その段階で指導した理解事項が,まだよくできていないからであるということが,すぐにいえる。しかし,初めの段階での評価をやめて,これを後の型の方程式について指導してから,一度にしようとすれば,その原因がどの理解の不足に基くかを,それだけでいうことは困難になる。
このようなことは,新しい理解事項が積み重なっていくときには,いつもいえることである。数学は,ほかの教科よりも,いっそうはっきりと,新しい概念が系統的に積み重なっていくようにできている。それゆえ,このような診断がすぐにできるようにするために,新しい理解が加わるごとに評価の機会を設けていくことに,特に気をつけることがたいせつである。
3.新しいことにはいる前に,必要に応じて,評価の機会を設けること
2.の説明では,いわば,診断を容易にするという立場から,新しいことが加わるごとに,評価をしていくというように表現されている。しかし,このように評価をして,それについての学習の成果をいちいち確かにしていくことは,けっきょく,次の段階の指導という立場から考えると,それに対する準備ができているかどうかをよく調べていくことにあたる。
この意味で,2.に述べたような評価がよくできていれば,次の指導にはいるための準備ということは,特別考えなくてもよいわけである。しかし,実際の指導においては,次の指導にはいるまでに,時間的に距離ができるようなことが多い。この点を考慮して,新しい事がらについての指導にはいるにあたっては,その基礎となる事がらについて評価する機会を設け,その指導にはいってよいかどうかを調べてかかるようにすることが必要である。
4.態度などについては,継続的な数多くの機会をとおして,評価すること
数学科の学習指導においては,数量的処理について,そのよさをわからせるとか,態度を伸ばすとかいうことは,重要な指導目標である。それに伴って,それらについての評価も,また,重要なことである。
すなわち,学習指導において,よさをわからせることをねらうのは,実際の生活において,数量的な処理をできるだけ有効に生かして用いるようにするためである。また,態度を伸ばすことをねらうのも,実際の生活において,学習したことを実践に移すようにするためである。しかも,これが気まぐれ方向な行為として現れるのではなく,社会的あるいは個人的に有意義に合致して,決まった傾向をもって現れるようにするためである。したがって,これらのねらいは,いずれも,単に頭の中で知っているということや,形だけ似た行為が表わされればよいということで満たされるのでなく,実際の場の条件をよく知って,それに対応して,適切な行為が実際に起ることを求めているものである。しかも,そのよさがわかるということも,態度ができるということも,1時間の学習ですぐに完成するというものではなく,多くの学習経験をもとにして,徐々にできていくものである。
この意味から考えて,評価をするには,適当な場において,実際にそのような行為が起るかどうかを見なければ意味がないし,1回だけの行為でなく,相当の時間にわたって,数多くの機会をとらえてはじめて,態度ができているかどうかを,帰納的に知ることができるのである。
たとえば,グラフを用いて,一次方程式の意味を理解させることを指導し,このときの学習活動をとおして,「グラフを用いると,方程式の根の様子を,一目でわかりやすく示すことができてつごうがよい」ということを,生徒にわからせることをねらったとする。
その結果として,この時間の終りには,A生徒は,教師に聞かれると,「グラフを用いると,方程式の根の様子が見やすくなる」と答えることができたし,また,B生徒は,実際に,一次方程式を解くにあたって,グラフをかいたとする。
これだけのことから,「AやBの生徒は,方程式を解くのにグラフを用いることのよさがよくわかっている」と考えてよいとはいえないであろう。
さらに,適当な時期に,次のような機会をとらえて確かめていくことが必要である。すなわち,AやBの生徒を,ある方程式の解法をクラスのものに説明させるために,黒板へ出してみる。そこで,はたして,この生徒たちが,グラフを用いて,皆にわかりよいように説明しようとするかどうかをみる。
また,やや複雑な方程式の解法を,レポートにして出させてみるような機会をつくる。このときも,グラフを用いて,わかりよく説明しようと心がけている様子が見えるかどうかを調べる。
このように,いくつかの機会をとおしてみれば,単に,気まぐれなものかどうか,わかりよく示す必要のあるような場合には,いつもグラフを用いていこうとする傾向があるかどうかを知ることができるであろう。
しかも,上のような場合には,単に見るだけでなく,指導も,もちろん必要なのである。もし,クラスの者が,式だけの説明でわかりにくいような表情をしているにもかかわらず,グラフを用いて説明し直そうとしないときは,まだグラフのよさがよくわかっていないと考えられる。そこで,その点をその場でも注意してやり「グラフを用いることによって,わかりよく説用できて,いかにも皆に満足感を与え自分も成功感を味わうことができた」というような経験をもたせてやるようにするとか,場合によっては,後にそのような指導の機会をつくることを考慮するとかする。すなわち,評価の機会と同時に,それを伸ばすための適当な指導が行われていくことが重要である。
このように,適当な期間をかけて見ていくと,さらに,次のようなことがわかる。生徒の中には,グラフを用いることは,ただ,人にわかりよく示すためにつごうがよいだけでなく,見慣れない方程式を解くにあたって,その解の見当をつけるのにもつごうがよいし,また,グラフに対応させながら方程式を解いていくと,考えがまとまりやすいということを知る者も出るだろう。そして,代数的に処理できるような場合にも,進んでグラフを用いて,直観的に解いてみようとくふうするようなことも起るだろう。
これは,グラフのよさをよくわかり,それを進んで用いようとすることの現れであると考えられる。このようなことを知ることは,グラフのよさについての学習の成果を単に知るだけでなく,次に,連立方程式や高次の方程式の解法を指導するために必要な,基礎的な能力を診断する上にも役にたたせることができる。
なお,態度などの評価を考えるにあたっては,次のことを考慮しておくこともたいせつである。
よさがよくわかっていると見られる行為をするにも,態度としてある傾向をもった行為をするにも,当然,ある理解や,ある能力が,そのもとになっている。それゆえ,それだけを単独にとりあげることは,できないことである。たとえば,上の例で,ある程度グラフを用いることのよさを感じていたとしても,グラフをかくことに自信のない生徒は,グラフを用いることを避けるであろう。すなわち,ある程度,グラフを用いる能力ができていなければ,それを評価しようとすることが,意味がないということを示している。このことは,また,上に述べたように,態度やよさを知ることを指導目標の一つの観点としてとりあげたねらいから考えても,わかることである。
5.心理的な考慮をして,適当に評価の機会を設けること
だれでも一つのことを長く続いて学習していると,初めのうち,よくわかったように思うことでも,そのうちにだんだん不安に思うようになることがある。また,わかりきったことでも,まとめをしないで,たくさんの事がらに触れていくと,しだいに,心理的に重荷を感じはじめるようになる。すなわち,注意の集中には限度があって,ある程度以上に長くなると無理が生じ,学習の能率があがらなくなるのが普通である。
このような場合に,適当なところで打切って,今まで学習したこと,これから学習しようとすることなどをまとめてやると,このような不安が解消され,自己評価を確かにする上にもつごうがよい。また,教師の立場からいっても,その指導したことを整理し,反省していくのによいことである。したがって,このような観点から,評価の機会を考えておくことも重要なことである。
実際に機会を設けるに当って,どれくらいの時間ごとにやったらよいとかいうことは,生徒の年齢,学習内容の難易や興味の度合などによって違う。それゆえ,その場の様子を察知して決めることが重要である。しかし,中学生ぐらいの年齢では,1時間のうちに,何回か切ることを考えていくようにするとよい。
これは,学習指導では,実際によく行われていることであるが,授業が混乱しそうなときなどには,特に気をつけて適切なくぎりを入れ,生徒も教師も,自己評価の機会をつくっていくことが必要である。
6.定期的な評価の機会を考慮しておくこと
毎時間,毎時間の学習の成果を,そのときどきに評価して,学習指導の改善に資していくことは,望ましいことである。しかし,それだけでは,全体的見地からの見落しがあったりしやすい。それゆえ,次のような観点から,定期的な評価の機会をつくって,補っていくようにするとつごうかよい。
(a) 個々に学習した,いろいろな面についての学習の成果を概観して,指導計画が,生徒の実際によく合っていたと考えられるかどうかを検討する。
(b) 毎時の学習の評価で,見落しやすいような学習の成果がなかったかどうかを考えて,そのようなものをとりあげる機会とする。
たとえば,比例の概念が図形概念と離れて指導された場合,図形の取扱いに関して比例関係を用いることについて,評価したかどうか。また,他教科と関連する部分で,その部分の評価が双方の教科で落ちたようなことはないか。あるいは,問題解決に関する能力の評価が落ちていないか。など
(c) 長期にわたる学習の成果と考えられる態度や総合的な能力についての評価の機会とする。
このような評価の機会を設けることによって,生徒に自己評価を促し,その機会を与えることができる。これによって,日常にあまり用いられなかったような技能について,それが低下するのを防いでいくようにすることもできる。
このような機会として,よく行われるのに,次のような場合がある。
以上のように,特別に評価のための機会を設けるのは,あくまで日常の評価の補助としてであって,これだけやれば,じゅうぶんであるというものではない。上に述べたような目的から考えて,どんなことについてすればよいかをよく考慮して,行うことがたいせつである。
Ⅲ.用具の選択
評価をするにあたって,教師のねらっている行為が,実際の学習の場合において生徒に現れたかどうか,また,期待するだけの行為が現れなかった場合には,どんなことがその原因になっているかなどということを,的確にしかも手軽に知るために,特別にくふうして用いる手段を,評価の用具ということにする。
従来,評価といえば,すぐにテストを思い出したように,評価の用具としては,テストが主として用いられているといってよい。しかし,テストは,紙に書かせて調べるものであるから,紙に書かせて容易にわかるような生徒の行為に対しては,用具としてつごうがよいが,数学科の目標としては,このようなものだけではないから,テスト以外の用具も考えなければならない。また,かりにテストを用いるにしても,ねらっていることが正しく表われるようになっていなければ,役にたたない。
このような意味から,まず,用具を選んだり,それをつくったりするときに一般に,どんな目安をもったらよいかを考え,次に,各種の用具をあげて,そのおのおのについての得失をあげてみることにする。
1.評価の用具を選ぶにあたっての一般的注意事項
用具としての使命から考えて,評価の用具は,大きくまとめて,次の二つの条件を備えていることが必要である。
A.使いやすいこと。
これは,それを用いるために,あまり大きな労力や時間が費されるようなことがないようにできていることである。すなわち,まず,つくりやすいこと,あるいは手にはいりやすいことである。次に手軽に用いられること,さらに,その結果の解釈が容易なことである。これらの条件は,用具であるからには,当然,必要なことであって,用具を選ぶときでも,また,たとえばテストを用いることに決めたあとでも,少しでも,それが使いやすくなるように,くふうしていくことが必要である。
B.評価のねらいにかなっていること
評価しようと決めた目標やその時間から考えて,そのねらいにあっているかどうかということである。いくら手数がかからなくても,ねらいにはずれていては役にたたないばかりか,かえって誤りを起すことにもなる。すなわち,使いやすいということも,ねらいにかなっていてはじめて,意味のあることであるといえる。
このねらいに合うように気をつけていくときの目安として,次のようなものがあげられる。
(1) 評価しようとねらった行為とは違ったものについて,調べていることにならないようにする。(用具の妥当性)
まず,ある用具でやることに決めた場合について,考えてみる。
たとえば,方程式で,移項の考えがうまく使えるかどうかを,テストを用いて評価することに決めたとする。この場合に,そのテストが,何題かの方程式を与えていて,その答が正しく出ているかどうかだけを調べるようになっていたのでは,そのねらいによく合っているとはいえない。
それは,方程式は,移項の考えを使わなくても解けるのであるから,たとえ,答が合っていたとしても,移項の考えができていることにはならないからである。また,たとえ,途中の計算も調べるようにしてあったとしても,方程式の係数が,生徒にあまり慣れていないような分数であったり,文字であったりすると,移項の考え以外のところに困難を感じて,その答や途中の計算に,移項の考えがどの程度に使われているかを必ずしも正しく反映することにはならない。このような場合には,係数はできるだけ簡単にしてやって,しかも,移項の考えが用いられる場合が,できるだけ豊富にしておくのがよい。
次に,用具自身がねらいに合っていない場合として,次のような場合が考えられる。
たとえば,問題解決の能力を,普通 応用問題といわれるものだけを与えて,評価しようとした場合である。
問題解決の能力をみる場合には,実際の場において,数量的な要因を見ぬいて,問題の焦点を明らかにしたり,数量的な処理ができるように,仮定を設けたり,条件を限定したりする働きをみることが重要なものとして考えられている。ところがこれらのものは,いわゆる書かれた問題の場合には,現れるような機会がほとんどないからである。どうしても,実践的な学習活動の場をとらえて評価しなければ,妥当なものとはいえないのである。
しかし,書かれた問題だけによった場合でも,次のような点で,問題解決の能力に関連したものが現れる。
(a) 数学的用語を含めた問題分を理解する。
(b) 問題文の中に含まれた数量的要素とその相互関係を認知したり,または理解したりする。
(c) それに対して,適当な計算法や公式を適用する。
(d) 計算したり論証したりする。
(e) 答が所要の条件に適するかどうかを検討する。
それゆえ,書かれた問題の解決の過程に,これらの能力が現れるにしても,単に答だけをみたのでは,これらの諸能力を総合した結果は知ることができても,個々の諸能力について,どうであったかをみることはできない。個々の能力について知るためには,評価の観点をそれに応じて分析しておいて,途中の過程もよくみていくようにすることが,ねらいに合った評価をするために必要である。
(2) 信頼できるような資料の得られるようにする。(用具の信頼性)
たとえば,「x/a=bの形の方程式を解くには,両辺に同じ数aをかければよい」ということが理解されているかどうかをみるために,テストで,x/3=6の方程式を解かせることにしたとしてみる。
このテストで,ある生徒がその答を2としたとすると,このテストの結果は,この生徒は,上でねらった事がらの理解が,まだできていないということを示すわけである。
確かに,この方程式x/3=6は,上の理解ができておれば正しく解けるはずである。その意味で,このテストはねらいと違ったことをみようとしてることにはならない。しかし,これだけの結果から,上の理解ができているとかいないとかを判断することが正しいであろうか。
すなわち,上のテストで,答を2とするものの中には,実際に上にあげた事がらを理解していない者もあるであろうが,たまたま,3が6の約数であることから,感違いして,6を3で割った者もあるかもしれない。このように,実際には理解していると考えられる者に対しても,反対の結論が出るようなことが起る。これでは,評価のねらいに合っているとはいえないのである。
そこで,もし,このテストの問題の中に,x/2=1/3やx/3=5などの問題も必要なだけ含めておくなどして,まぎらわしい場合が除けるようになっておれば,理解のできているもの,感違いをしたもの,理解のできていないものに対しては,いつもそれに応じた結果が出るようになる。すなわち,その結果は,信頼できることになる。このようになっていて,はじめて,的確な判断ができ,評価の用具として役にたつのである。
一般的にいって,評価に際して,ある判断を下すにあたっては,常に一つの行為だけでなく,それに関連のある多くの行為を資料とし,それをいろいろの角度からみるなどして,できるだけ客観的に判断が下せるように,くふうすることが必要である。
(3) 既製のテストを用いるときには,それがつくられた目的を考えて,各自のねらいに合う資料の得られるものを用いるようにすること。
テストには,いわゆる,診断テストとか,アチーブメントテストとか,知能テストとか,使う目的によって,いろいろのものがくふうされている。これらを用いるにあたっては,評価しようとする目的や時間から考えて,各自の目的にかなったものを用いることが必要である。
たとえば,ある学級で,一定の期間に指導したことが,どの程度,生徒に学習されたかを知るためにテストをすることにしたとする。このテストを用いる目的は,その結果,生徒の学習の成果が予期に反して悪いことを見いだした場合には,その原因を知って,次の指導に進むまでに治療してやろうとすることにある。それゆえ,上の目的に合う診断に役だつことが必要である。ところが,このテストとして,全県的につくられたアチーブメントテストを用いることにしたとする。このようなアチープメントテストでは,一般に,各個人について,どの技能とどの技能とができるかを知ったり,それをもとにして,全体的な平均を求めて,指導効果を全体的につかんだりするのにつごうよくできている。しかも,個々の学校で指導したことなどを,あまり考慮したものではないのである。それゆえ,このようなアチーブメントテストなどを用いても,その学級の生徒に対して,上の目的で診断するのには,あまり役にたたないといえる。
また,能力別に学級を分けて,ある技能を指導しようとするのに,知能テストだけを用いて,その結果によって分団別に分けようとする場合について,考えてみる。
このように,特定の技能を指導するのに分団別に分けるのは,その技能についての基礎となる理解や能力がどの段階にあるかをよく知って,それに応じて分けておくと,生徒の実際に合うように指導をするのにつごうがよいと考えられるからである。
たとえば,百分率の計算について,指導するのに,割合や,百分率についての理解や小数・分数についての計算がどの程度であるかを知って,その程度に応じて分団に分けておくと,各分団で同じ程度の指導ができて,指導の能率を上げることができる。
しかし,これを知能テストの結果だけで分けておくと,百分率に関係なく一般的な理解のしかたなどについては,ある程度同じような者を集めることができるかもしれないが,一つの分団の中に百分率についての基礎的な理解の違ったものが混じるようなことが起る。それゆえ,上のような意味で,指導の上に,必ずしも手数を省くことにはならないのである。
(4) 診断に役だつものを用いる。
学習指導において評価をするのは,なんらかの診断ができることをねらっているのである。すなわち,その結果に基いて,次にどんな指導が必要かの目安がたつことが必要なのであって,単に,優劣をみるだけではないのである。これは,理解や技能については,もちろんであるが,能力や態度について評価するときにも,必要なことである。
たとえば,測定をするときの態度を評価するのに,次のような尺度を用いたとする。
|—————————|—————————|—————————|—————————|
非常によくない よくない 普通 よい 非常によい
このような尺度で結果が得られたとき,一般に,優劣をいうのにつごうがよいかもしれないが,指導の目安をつけるのには,あまり参考にはならないといえる。
それゆえ,上のような量的な程度を表わす尺度を用いようとするときには,各段階に対応して,その段階にあたる者に対する指導の目安が,具体的にあげられるように,観点を選んでおくことが必要である。これに対して,たとえば,次のように指導の観点をいくつか具体的にあげておいて,できたもの,できないものをチェックして記録していくようなものを用いると,つごうがよいと考えられる。
〔測定をするときの態度について〕
○ (a) 検定の合否を確かめてかかるか。
× (b) 測る目的に対して,精度を考えて用いているか。
○ (c) 零点や基準を合わしてかかるか。
○ (d) 目もりや分銅などをいためないように注意している点がみられるか。
? (e) 使い方の指示のある計器は,それを読んでから使うか。
× (f) 容量以上のものを測ったりしないか。
○ (g) 保存に気をつけている点がみられるか。
(h) ………
要するに,評価をするに際して,どんな目的で用具を用いようとしているのかを考えて,評価のねらいに合った資料の得られるようなものを選んだり,つくったりすることが必要である。
2.数学科の評価で用いられる各種の用具とその得失
評価の用具としては,いろいろのものがくふうされているが,これを,生徒に書かせることによって評価するものと,生徒に話させることによって評価するものとに大別して,述べることにする。
A.書かせることによって評価するものについて
これに該当するおもなものには,次のものがあげられる。
Ⅰ.筆答テスト(ペーパー・ペンシル・テストともいう)
Ⅱ.レポート
Ⅲ.質問紙
Ⅳ.チェックリスト
Ⅴ.ノート
Ⅵ.個人的な諸記録
書かせることによって評価する場合のつごうのよい点は,いずれも,記録が残るということである。すなわち,一般に,次のような点でつごうがよいといえる。
(a) 資料として残すための記録の手数が省ける。
(b) 生徒の話を聞いたり活動をみたりするように,瞬間的に変るものに基いて評価するのでないから,特別な熟練や緊張を要せず気楽である。
(c) 多数の生徒に対して,同時に適用することができる。
(e) 自分の考えた経過や結果が残っているから,自己評価の資料として生徒にも教師にも,役だつ。
このようなつごうのよい点があって,非常によく利用されるが,その反面,次のような事がらに注意していくことが必要である。
(a) 一般に,生徒の応答に応じて,発問を変えていくようなことができないから,能力差に応じて幾種類かのものを用意するとか,用いる時期を考慮して,それを失しないようするとかなどのくふうをしないと,生徒の実情に合った資料が得られなくなる場合が起こる。
(b) 評価の資料としては,一般に,このような書かせたものだけに頼りやすい。書かせることだけでは知ることのできない目標があることを念頭において,常に目標を吟味しながら,これらの用具を用いるようにする。
〔Ⅰ〕 筆 答 テ ス ト
これは,最もよく用いられるものである。そして,非常に使いやすいものであるだけに,それだけ,陥りやすい欠点も多いから,使用にあたっては,じゅうぶんの注意が必要である。
筆答テストには,いわゆる,論文式のもの(……について説明せよとか,次の問題を解けとかいう形のもの)と客観形式のものとがある。
論文式のテストでは,計算をしたり方程式を解いたり,あるいは応用問題を解いたりさせた場合に,それらのことが正しくできるかどうかを,途中の経過や結果の答などをみて,総合的に知ることができて,つごうがよい。しかし,その中で用いられる個々の理解だけをとりあげて知ろうとする場合には,不便なことが多い。また,相当に長い文章を要するようなときには,生徒の表現力いかんによっては,知りたい理解や技能が,ゆがんで表われることがある。
これらの点を考慮して,客観テストの形式がくふうされ,よく用いられている。これには,次にあげたような種々の形式のものが考えられている。
〔客観テストの種々の形式〕
(a) ○1貫は何キログラムか。 答
○y=x+3のグラフのこうばいは,どれだけか。 答
……
という形式で,簡単な答を思い起させて,記入させるもの(再生法)
(b) ○円の面積は,半径と□とがわかれば,計算で求められる。
○測定値をかけ合わせるときには,測定値の□をそろえることが必要である。
……
という形式で,簡単な答を,□の中に記入させるもの(完成法)
(c) (a)や(b)のやり方で,まぎらわしいいくつかの答の例をあげておいて,その中から,正しいものを選ばせるようにしたもの(選択法)
または,これを変形したものとして,
○一定の時間に歩く速さと進む距離
○一定のおかねで買える品物の個数とその単価
○鉛筆の減った部分の長さと残った部分の長さ
……
などの,一つの数学的概念からみて類似いくつかの関係を与え,この中から,正比例・反比例などに該当するものを選ばせるようにしたもの。
(d) ○等式の両辺に同じ数をかけても,その等式はなりたつ。
○等式の両辺を,どんな数で割っても,その等式はなりたつ。
……
という形式の文章を与えて,その正否をいわせるもの(真偽法)
(e) (d)のようなやり方で,ふつごうの個所を指摘させ,その理由をいわせるとか,それを正しいものに訂正させるとかするもの(訂正法)
(f) ○方程式を立てる。
○未知数を決める。
○答が適当かどうかを吟味する。
……
という形式の一連の文章を与え,それらの順序をいわせるもの(配列法)
(g) ○円グラフ ○量の変化を表わす
○棒グラフ ○量の大きさを表わす
○折れ線グラフ ○量の割合を表わす
……………… ………………
上のような二つの系列の文章を与え,意味や使い方の上からみて,関速のあるものを,組み合わせるようにしたもの(組合せ法)
(h) 単位分数を,分数の,加法や減法を,書かればよい,そろえて,するには,……
というように,一つの文章をばらばらにしておいて,その文章を完成するようにしたもの(作文法)
このほか,これらの二つ以上を組み合わせるとか,これらを数式の場合に合うように変形するとかして,いろいろの形のものか考えられている。(上の例で,( )の中に入れた名称は,必ずしも,決まったものではないが,形式をいう場合の便宜のために,普通によく用いられているものを入れたのである。)
〔筆答テストを用いるときの二・三の注意〕
① 論文式テストと客観テストの優劣
筆答テストについて,客観テストがよいとか,あるいは,客観テストではほんとうの能力がわからないとかといわれているがどちらが適当かということを,一概にいうことはできない。
これを,テストをつくる手数からみると,論文式のものが,客観テストに比べて,簡単でよい。しかし,その結果を処理するときの手数では,後者のほうがすぐれている。
次に,目標によく合った資料をとることができるかどうかという点からみる。上にあげたテストの例でもわかるように,客観テストでは分析された個々の理解事項や技能をみるには,つごうがよい。これは,客観テストがくふうされた主旨からみれば,当然のことであるともいえる。しかし,自主的に問題を構成したり解決したりするときに現れる,創造的な思考過程やそれについての能力は,客観テストの形式だけで知ることは,なかなか困難である。それは,答の形式や表現のしかたが,強く縛られているからでもある。
もちろん,客観テストでも種々研究がされて,ある程度までは,総合的な能力もみることもできるものがある。このようにくふうされた形式のものは,入学試験とか,大規模な調査などのように,個々の被験者に対する実情は,ある程度無視されても,採点の客観性や結果の処理における迅速性が強く要請されるような場合には,有効な方法である。しかし,学習指導の場合のように,実際の指導に合ったように,いちいちテストをつくることが必要であるような場合には,手数からいっても,技術からいっても,それを利用することはなかなか困難なことである。
次に,論文式テストを用いると,上のような能力が容易にわかるかというと,必ずしもそうではないのである。いずれも,紙に書かせるテストであるから,そのことからの制約はあるが,論文式テストの場合には,解答のしかたに,自主的創造的な面が現れやすいことは,確かである。しかし,テストの結果を解釈する場合には,特別のくふうが必要とされるのである。前にも述べたように,答だけをみて評価するのでは,そのよさが生かされることにはならないのである。
② 客観テストを用いるときの注意
客観テストは,上に述べたとおり,新しくくふうされたもので,評価の用具としては,有効なものである。しかし,その主旨を考えないで,単に,形式だけをまねただけでは,このテストのよさを生かしていくことはできない。これについて,注意すべき二・三の点を,次にあげてみる。
(a) ねらいを明らかにしてかかること。
客観テストでは,どんな数学的目標をねらっているかが,はっきりしないものがよくある。これは,完成法に,特に,多い。
客観テストを用いるにあたっては,まず,どんなことを測ろうとするかを明らかにしてかかることが重要である。次に,完成法による場合であったら,□の部分を埋めた文章が,ねらいとする数学的理解事項を,なんらかの形で表わしているようにすること。さらに,□の個所を決めるにあたっては,その中にどんな文字を入れたらよいかが,そのねらいとする理解事項に基いて判断されるようなものにしておくことなどに,注意することが必要である。
たとえば,利まわりについての理解事項として,「利まわりは,時価の高低にかかわらず,どの株が有利かを調べる一つの目安となる」ということを理解しているかどうかをみようとしたとする。
これを,完成法でテストしようとして,次の文章をもとにすることにした場合を考えてみる。
「一般に,配当率のよい株は,時価が高くなってたり,配当率の低い株は,時価も安くなっているので,配当率,あるいは,時価だけで,どの株が有利かはわかりにくい。
そこで,利まわりをみると,どれも大差ないようになっていることが多いが,その大小で,どれが有利かをみる一つの目安になる」
そこで,問題をつくるにあたって,次のようなところに,□を設けたとする。
(イ) 一般に,配当率のよい株は,時価が□なっており,………
(ロ) 一般に,配当率の□株は,□が高くなっており,………
この(イ),(ロ)の例は,いずれも,初めにねらいとした,利まわりの概念をみているというよりは,時価と配当率との関係を問題にしていることになる。したがって,妥当な問題とはいえなくなる。また,特に,(ロ)のように,一つの文章の主部と述部とに□をおくと,テストが「あてもの」に近くなり,必要以上のところに混乱を与えることとなる。このことによって,信頼性もなくなる。
また,次のようなところに,□をおいたとする。
(ハ) そこで,利まわりをみると,どれも□ようになっていることが多いが,その大小で,どれが有利かをみる一つの目安に□。
この(ハ)における□は,いずれも,利まわりの概念をみるには,よい場所であるが,前の□は,「どれも」ということばがあるために,「大差ない」,「大差がある」のどれにすればよいかが,国語の感じから,わかる。また,後の□についても,前文が,「……が」という逆態接続を表わす助詞があることから,また,文章自身の感じからいっても,目安に「なる」,「ならない」のどれとすればよいかがわかる。
このように,数学科以外の,国語の判断力でわかるようになっていても,数学科のテストしては妥当とはいえない。
(b) 信頼性を高めるようにすること。
客観テストでは,一般に,偶然的な的中が起りやすい形式になっているものが多い。これは,真偽法が最も大きいが,選択法や配列法でもそうである。
これを避けるためには,問題によっては,単に正・否をいわせるとか,正答を選ばせるだけにしないで,その理由となることやそれから必然的に生ずる事がらもあげておくなどして,各自の選んだ解答と,つじつまの合った解答ができるかどうかも,みるようにしておくのがよい。
たとえば,
○測定値について積を計算するときには,それらの{正さ くわしさ}をそろえてかかるとよい。
という問題について,「正しさ」と「くわしさ」のどれかを選ばせたなら,さらに,次のような問を出しておいて,それについても,正しいと思われるものを選ばせるようにしておく。
○幅3.8メートル,長さ243.3メートルあった直線の道路の面積は,次のどの式で計算するのがよいか。
□243.3(m)×3.8(m),□243(m)×3.8(m),□240(m)×3.8(m)
上に述べたような方法をとることができないとき,選択肢を多くしていくことも,偶然的な的中率を少なくするのによい方法である。しかし,この場合,そこに並べる各選択肢が,目標とする数学的な内容からみて,類似なものでないと,いくらふやしても意味がないのである。
たとえば,折れ線グラフは,どんな場合に用いるとつごうがよいか,次にあげたいろいろな場合から,選ばせるとする。
(イ) 通学に要する時間を,30分ごとにくぎって,各くぎりにはいる者の人数を比べる。
(ロ) 各区域から通学する者の人数を比べる。
(ハ) 各区域の通学者の割合を,各学年で比べる。
(ニ) 自転車通学者の人数が,年々どんなに増えたかを表わす。
……
としておいて,選択肢を多くするために,次の場合を入れたとする。
(ホ) 各学年の通学区域を表わす。
この(イ)から(ニ)までは,どれも,数値をグラフに表わす場合であるが,(ホ)はそうではない。この点から,(ホ)が適当かどうかは,(イ)ないし(ニ)の場合とは,違った見地からの判断でできることになる。
これと同じようなことは,組合せ法で,二つの系列をつくる場合にも注意しなければならないことである。
要するに,どんな客観テストをつくるにしても,まず,どんなことをねらうかをはっきり決めてかかり,それに合うようにするように,気をつけることが必要である。そうでないと,いくら,結果が出ても,使いものにならないことになる。
〔Ⅱ〕レポート
レポートは,筆答テストと同じく,生徒に書かせることによって,評価しようとするものであるが,筆答テストに比べて,生徒に時間的な制約を与えたり,参考文献の引用を妨げたりしないで,その考えを自由に表わすことができるようにしたものである。
レポートは,次のような場合によく用いられるようである。
(a) ある主題を与えておいて,それについて,研究したことをまとめて提出させる。
(b) 全体の学習でとりあげたことから,さらに発展した研究を個々にやった結果をまとめて,提出させる。
(c) 自己評価を促す意味において,ある期間に学習したことの要点をまとめて,提出させる。
(d) 研究計画の実施にあたって,研究しようとする事がらの概要やその方法を評価するために,その要点をまとめて,提出させる。
レポートをつくることは,学習活動としても重要な意味があることであって,単に評価の用具としてとりあげられるだけのものではない。レポートを評価の立場から考えると,それは,教師の作為的な発問にだけ答えるものではないから,生徒が自主的に,問題をはあくしたり,解決のための論理を進めたりするときにおける能力や態度,およびその内容に表わされる創造的な面などをみる資料として,有用なものであるということができる。
しかしながら,それは,自由度の大きいだけに,これを評価の用具として有効に用いるためには,評価の観点を明確にしておくなどの,特別のくふうが必要である。これがよくできていないと,字のきれいであるなしとか,主題に対する教師の興味のあるなしとか,結論が教師に気に入っているとかなど,およそ,数学科の指導目標とあまり関係のない事がらにとらわれて,評価しようとする事がらから,はずれるようなことが起りやすい。
たとえば,「こづかいの使い方」について学習したあと,各自の研究をまとめて,レポートを書かせた場合について,この注意を述べてみよう。
まず,このレポートをみるにあたって,どんなものが評価されるかを考えておくことが必要である。この場合には,評価の観点として,次のようなものが考えられるであろう。
(1) 数量的な処理に必要な要素についての理解かできているか。
(a) バランスの考えを用いているか。
(b) 適当な項目(費目)にまとめているか。
(c) 金額だけでは,つごうの悪いときに,割合を用いているか。
(d) 計画に対しては,適当にまるめた数を用いているか。
(e) 予備に対する考慮がしてあるか。
(f) ……
(2) 論理の進め方が合理的であるか。
(a) 仮定したことや条件となることを,はっきりと示しているか。
(b) 結論が,その仮定や条件に対して,矛盾したものになっていないか。
(c) 各段階で調べたことに対して,評価がよくできているか。
たとえば,ある段階でうまくいったことを生かそうとしているか。また,うまくいかなかったことに対して,考慮を払ったあとがみられるか。
(d) 各項目に割り当てる割合や金高を出すときの推論が妥当であるか。
(e) ……
(3) 創造的な態度が現れているか。
(a) 全体の表現に,簡潔さ,わかりよさなどの点からみて,くふうされたあとがみられるか。
(b) 個々の事がらの内容について,学習でとりあげたとき以上に研究したあとがみられるか。
(c) 研究に用いた方法が,学習のときに用いた方法以上にくふうしたものであるか。
(d) ……
レポートをみるにあたって,ここにあげたような観点を明らかにしておいてはじめて,評価がしやすくなると考えられる。しかし,実際には,このままでは,なお困難であって,さらに各項目をもう一段と具体的にしたものがあることが望ましい。これは,目標をはっきりとさせる場合に,具体的な事例をよく考えておくことがつごうがよいと同じことである。
すなわち,(2)の(d)で,「割合や金高を出すときの推論が妥当であるか」といっただけでは,あいまいである。たとえば,次のようなことが,その裏にはっきりとつかまれていることが必要である。
さらに,この前者に対しては,
(ⅰ) 期間に対して考慮することなく,単に,有合せの資料だけについて考えたもの
(ⅱ) 期間に対して注意はしたが,単に長ければよいと考えて,相当の期間についての平均を用いたもの
(ⅲ) 計算のつごうを考えて,1年とが2年とかのきっちりとした期間を用いたもの
(ⅳ) 物価の変動などから考えて,現在に最も妥当するとみられる期間を選んでとったもの。
(ⅴ) 各項目の割合が,月や学期によって,ある程度の違いがあることに着目して,期間も適当にくぎってとっているもの
などのような具体的な事例がつかまれていると,つごうがよいわけである。しかしながら,このように,観点を具体的に細かくすることはつごうのよいことではあるが,いたずらに細かいばかりがよいというわけにはいかない。これは,単に,そのよしあしに応じて,採点をしたり,その種類によって分類したりすることが,目的ではないからである。評価としてとりあげるからには,その一つ一つの項目に対応して,その項自に該当するものには,こんなことが指導されなければならないということが予想されていなければならないのである。それゆえ,どのように分けておけばよいかということは,どの程度に分けておいたら次の指導につごうがよいか,という見地から考えられることである。この点から考えると,あまり分けすぎても,指導がそれに伴わないで,せっかくの努力がむだになることが起るわけである。また,これと同様の意味で,一つのレポートについては,上にあげた全部の観点について,評価しなければならないというわけではない。あまり多くの観点から,一度に評価しようとすることは,非常に困難なことであるから,場合によっては,指導のときに主としてねらったことがらを中心にして,二・三の項目だけを選んで,それについて評価するようにするがよい。
また,このように,前もってとりあげた評価の観点は,最後まで固守されるべき性質のものではなく,実際のレポートを見ているうちに,とりあげて指導したらよいと思われるような事がらが出てきたり,観点として,初めに見落していたりした事がらに出会ったときには,必要に応じて,それをとりあげるようにしていくがよい。
〔Ⅲ〕質問紙
面接して質問する代りに,紙に書かせるようにしたものである。これは,筆答テストのように,学習の成果を調べるというよりは,生徒の興味・関心・経験あるいはその環境などについて調べる場合に,よく用いられるようである。しかし,これを,家庭や社会の人たちと協力して,学校外における生徒の行為について知ることに用いると,学習の成果を知る上にも,非常に有用なものとなる。
たとえば,学校で,こづかいの使い方について指導した後,次のような質問紙を家庭に送って,生徒が,日常生活に実際に用いるようになったかどうかを知ることが考えられる。
(a) こどもは,こづかいについて,どんな処理をしていましたか。
□こづかいについて,特別の関心を示したことがない。
□こづかい帳をつけていた。
□こづかいを自分で貯金していた。
□こづかいを親にあずけていた。
(b) こどもに,こづかいをどんなやり方で与えていましたか。
(c) 最近,こづかいの使い方について,学校で指導しましたが,それについて,こどもに何か変ってきた様子がみられませんか。
□全然変ったことがみられない。
□毎月一定額のこづかいを要求するようになった。
□多くなった
その額は,今までより □少くなった
□たいして変らない
□こづかい帳をつけるようになった。
□こづかいを自分で貯金するようになった。
□その他。
(d) 家計について,関心を示すようなことはありませんか
□全然ない。
□こづかいに関連して,ときどき意見をいう。
□家計のやり方に対して,意見をいう。
(e) こづかいについての指導したことについて,どう思いますか。
□よかった。
理由 □むだ使いをしなくなった。
□無理な要求をしなくなった。
□安心しておかねを与えられるようになった。
□その他,簡単な理由( )
□よくない
理由 □家計について,余分なことをいうようになったから。
□家庭によって事情が違うから,あまり意味がない。
□その他,簡単な理由( )
質問紙を用いるにあたっては,ありのままの答が得られるようにするためと,回収を容易にするために,次の事がらに注意することが必要である。
(a) 他人に知られたくない事がらに触れるときには,それによって,その人が不利になるようにしないことを約束しておくこと。
(b) 答は,「はい」,「いいえ」とか,単に記号をつけるなど,できるだけ簡単に答えられるような形式にしておくこと。
(c) 質問をする事がらは,深く考えないでも,簡単に答えられるような事がらに関するようにしておくこと。
(d) 答え方とか主旨とかについて,あまり長い文を読まなくても,できるようにしておくこと。
〔Ⅳ〕チェックリスト
チェックリストは,形式は質問紙に似ている。しかし,これは,他人に対して質問するときにもよいが,自分で手落ちや足りないところがないかどうかを調べる用具として,有用なものであると考えられる。
すなわち,次のような場合に用いると,つごうがよい。
(a) 計算の手順などを,順次にあげておいて,自分がどの手順でまちがえているかを明らかにする。
(b) 測定などの手順を示しておいて,その手順をまちがえないように照合するのに用いる。
(c) 研究や指導の計画にあたって,準備すべきことや考慮すべき事がらをあげておいて,それらがそろっているかを照合するのに用いる。
たとえば,次のチェックリストで,小数を割る計算をするときに,どんな考えを用いて計算を進めるか,その順序に問をあげたものである。これで,小数を割る計算で,どんなところの理解がよくできないかを自分で知ることができる。すなわち,順次,問に自分で答えていき,どの問で答えられないかがわかれば,そこが自分の理解の不確実なところである。
(ⅰ) 商が小数になることは,どうしてわかるか。
(ⅱ) 商の小数点の位置は,どうして決めたか。
(ⅲ) 商の初めの数字が0であることは,どうしていえるか。
(ⅳ) 商の次の数字の7は,何を何で割ったものか。
(ⅴ) 32×7=224の4を,2.4の4より一けた右から書くのはどんなわけか。
(ⅵ) 引き算の余り16は,何から何を引いてでた数か。
(ⅶ) 16の右に書いた0は,どこからおろしてきた0か。
要するに,このチェックリストの考え方は,教師にとっても,生徒にとっても,自己評価をするのに有効なものであるから,各自のまちがいやすいところなどに対して,このようなものをいろいろとくふうしておき,それを用いるようにすることが望ましい。
〔Ⅴ〕 その他の用具
ノートやその他,生徒の個人的な記録は,そのままでは有効な評価の用具とはいえないが,適当に用いていくことによって,テストやレポートなどではみられない生徒の行為を知ることができる。
これについては,たとえば,次のような例がある。
ある学校で,毎時間の授業の終りに,順次に5名ずつの生徒にノートを提出させる(5名と決めているのは,一度に全クラスの考えについてみることが,時間的に困難であるから)
このノートについて,次のような観点で評価することにしている。
これによって,生徒はよく自己評価してノートをとるようになり,教師も,テストや日常の観察では気がつかないような,個々の生徒の実情について,よく評価することができるようになったという。
要するに,このような記録によって評価することは,非常に有効なものであるが,レポートの場合と同じように,評価にあたっては,どんな観点から評価していくかをはっきりと決めてかかることがたいせつである。また,このような仕事は,一時は熱心にやっても,すぐにとだえやすいものであるが,そのようなことのないように,継続的にやるように努めることが必要である。
B.話させることによって評価するものについて
評価の手段として,生徒に話させる場合として,次のものがあげられる。
Ⅰ.発表 Ⅱ.面接
Ⅲ.質問に答えさす,発問をさせる。
話させることによって評価する場合は,書かせる場合に比べて,その場の状況に応じて生徒を選択したり,生徒の応答のいかんに応じて,発問を加減したりしていけるという点で,つごうがよい。また,書くことを要しないから,特別に用紙などを用意する必要がないし,生徒に割合に固苦しい感じを与えないで済ますこともできる。
この反面,次のような点に,特に注意を要する。
(a) 全部の生徒に答えさせるような場合には,多数の生徒に引きずられて,少数の生徒を見のがしやすい。
(b) ひとりの生徒に発表させるような場合,生徒によっては,発表することに心理的な重圧を感じることが多いから,この点を考慮する。
(c) 特定の生徒に片寄って発問したり,発問の内容があまりにも特殊な事がらに片寄ったりすると,他の生徒を遊ばせることになりやすいから,他の一般の生徒の自己評価にも役だつように考慮する。
(d) 特に参考によると思われるものは,メモしておいて,後の評価の資料にするようにする。
〔Ⅰ〕発 表
ある主題についての研究や,問題の解法などを発表させることをとおして評価するのが,これにあたる。
発表の場合にも,レポートの場合と同じように,総合的な能力や態度などをみるのにつごうがよいが,その内容や方法に生徒の自由性の多いものであるから,評価の観点をはっきりとつかんでかかることが重要である。要すれば,教師が,それをチェックリストのようにして,持っているとよい。
さらに,発表は,自己評価の手段としても有効である。
たとえば,方程式など,一応,形式的に解けても,それを黒板で説明させたとき,ちょっとでも理解の不確実なところがあると,なかなか,人にわかるように説明できないものである。それによって,その生徒は,自分のよくわからない点を浮び出させることができる。たとえば,
x−1/3+x/2=1という方程式を
2(x−1)+3x=1
………
として解いた生徒がある。
この過程を説明するにあたって,「まず,両辺に3と2の最小公倍数6をかけて,……」といいかけて,右辺に6をかけるのを忘れたこと,あるいは,自分は0と1とをまちがいやすい癖があって,このときも,右辺が0であるときとまちがえたことなどを認めることがよくある。
また,これに対して適当に質問を発して,ふめいりょうな点を明らかにしてやったり,あるいは,他の生徒に発問させ,同時に全体の生徒についても評価させたりするようにすると,発表を評価の用具として,いっそう有効に利用できる。
〔Ⅱ〕面 接
面接は,質問紙のように形式ばらないで,個々の生徒に対して,気楽に納得のいくように話し合うものである。この意味で,質問紙の場合のように,興味や家庭環境についての事がらを聞くときは,もちろんであるが,筆答テストの答案などについて,誤りの診断をさらに深くするときなどに,面接を行うとつごうがよい。
たとえば,計算の途中に,67×8=356としたために,その問題を誤っているような場合に,これをとりあげて,どんな順序に計算したかをいわせてみる。その結果,もし,次にあげたような説明をすれば,その生徒は,最初の部分積の十の位の数字を,次の部分積を求めるときの乗数にしたことがわかる。
| 七八 五十六として, 56をかき,
五十六の五を67の六にかけて,
五六 三十 だから,
56
+30 の計算をして,356とした。 |
この自分の説明をとおして,まちがいであることにすぐに気がつけば,単なる感違いと考えてよい。そうでない場合には,その誤りであることを理解させるために,さらに,その基礎になる理解事項がわかっているかどうか,たとえば,「67の各数字は,それぞれ,どんな単位をもっているか」「それに8をかけるということは,どんなにすることか」などについて,発問をしていくようにすれば,その原因を知ることができる。
要するに,この面接は,普通の学習指導でよく行われていることであるが,生徒のした行為について,何かふにおちないようなことがあれば,すぐに,この方法をとるように,気をつけていくことがたいせつである。
〔Ⅲ〕質問に答えさせたり・質問をさせたりする
生徒に質問をしたり,生徒から質問を受けたりすることは,評価の方法として,最も普通に用いられるものであるが,次のようなことについての注意が必要である。
(a) 「よくわかったか」とか,「わかったね」とかいう発問をして,生徒に単に,「はい」とか「いいえ」とかの応答を要求する場合をよく見受ける。ところが,問題によっては,このように答えられない場合もあり,生徒の中には,よくわかっていなくても,どこかよくわからないかがいえないので,「はい」といってごまかしてしまったりすることがよくある。
相手の生徒についての状況がよくわかっていて,理解の程度が,顔色その他でよくわかるか,あるいは,黒か白かがはっきりいえるかする場合のほかは,できるだけこのような発問を避けて,一つの文章で答えさせるようなものにする。
この場合,「……だから,……である」という形式の答をいわせるように気をつけるのも,一つの方法である。
(b) 生徒が発問できるというのは,ある程度自己評価ができているという証拠であり,その発問が筋に合ったものであるかどうかによって,自己評価の程度を知ることができるものである。
したがって,学習指導においては,できるだけ発問の機会を与えるようにしてやることが必要である。しかし,内容がよくわからない場合には,発問もできないものであるから,このような場合には,適当に教師のほうから,その要点を思い出すような質問を発して,自己評価を促してやることが必要である。
(a)でとりあげた「わかったか」とかいうことばは,との発問を促す一つの手段としては,よくとられる方法である。
以上,評価の用具として,いろいろの例をあげた。実際に評価で用いるにあたっては,それらの形にとらわれることなく,評価しようとするねらいとよく合うように,おのおののよい点を生かして,いくつもの用具を組み合わせるとか,形を変えるとかして,絶えずくふうして用いるようにすることが,たいせつである。
Ⅳ.資料の記録
資料を記録しておくことは,次のような点で,評価をする上に必要なことである。
(a) 学習の成果のうちには,長期にわたってみていかなければ評価のできないものがある。このようなものに対しては,ときどきの資料を記録して,保持していくことが必要である。
(b) 一時には,解釈のできなかった生徒の行為の中には,後になって意味がわかってくるものがある。このような,問題を含むと思われる行為を記録にとめておいて,後で評価する資料とすることが必要である。
(c) 学習の成果を適当に記録しておくと,生徒の成長について外部に対して報告したり,指導要録を作製したりするために,特別なテストなどをする必要がなくなる。
(d) 長期間の進歩の状況を概観して,指導計画の改善をはかる上に役にたつ。これは,また,同時に,生徒が自己評価するのにもつごうがよい。
このほか,生徒の行為をできるだけ記録にとめておいて,多くの資料に基いて評価をするようにすることは,評価を客観的にする上に,必要なことである。
このようなねらいに合うように,記録をとるには,次のようなことに注意することが必要である。
(a) 評価するに際して,有用な資料となる見込のあるものだけを記録するようにする。記録のためのノートをつくるときは,この点を考慮して,評価のねらいからみて,あまり必要と思われない項目は,できるだけ避けるようにしないと,むだに労力を使いやすい。
(b) 記録のために,特にくふうしたノートなどを準備しておいて,資料をまとめておくようにする。教科書やその他のものに,思いつきを単に書きこんでおくだけでは,必要なときに,有効に使用することができない。
(c) 評価は,時に応じて行っていかなければならないから,特に資料が使いやすいようにその形式をくふうしたものでないと,間に合わないし,長続きもしないものである。この意味から,各自に,最も使いやすいと思うものをくふうして用いるのがよい。
(d) 記録に際して,記号などを用いて,記述を簡単にすることは,便利なことである。しかし,これは,よく起るものに限るようにして,記号の種類などを,あまり複雑にしないように注意すること。
記録のしかたとしては,各自に使いやすいものをくふうして用いるのがよい。次に,これを考えるときの参考として,二・三の実例をあげておく。
〔例1.〕 これは,ある上級の学校の教師が,用いた一例を示したものである。

この方法は,ある学年の一学期,または一学年分についての指導内容の概要および評価の記録を,一冊のノートにまとめることにしたものである。その一時間分の指導には,上に示したように,ノートの見開き2ページ分を用いることにしている。この使い方を説明すると,次のようである。
(a) 右のページには,その時間の指導計画の概要を学期,または,学年の初めにたてて,それを記入しておく。
(b) 左のページは,だいたいに中央で上下二つに区分する。その上半は,次のように利用する。
① その時間の指導に関して,注意を要すると思われる生徒の氏名とその内容を,計画をたてるとき,およびその後の指導で気がついたときに記入する。
② その時間の指導を終えたとき,上にあげた生徒について評価した結果を記入する。このとき,以後の指導で引き続いて注意する必要があったら,該当するページのこの欄に必要事項を記入する。
その下半は,次のように利用する。
① 右のページに書いた指導内容を指導するに際して,指導方法として注意すべき事がらを記入する。
② その時間の指導を終えたとき,指導方法や指導計画について,反省した事がらを書く。このとき,以後の指導に関することがあったら,該当するページのこの欄に記入する。
この方法を利用するにあたっては,次のようなことに注意することが必要である。
(a) できない生徒に対してだけでなく,よくできた生徒に対する記録もとるようにする。
(b) 見開き2ページ分が,うまく1時間ごとに割り当てられるように,教科書などを参考にして,指導のくぎりをよく考えておくこと。
この方法では,毎時間の指導で,注意すべきことが一目でわかるようになっているから指導や評価の手落ちを少なくすることができる。また,左のページを次々にめくっていくと,各人の評価の記録がひとりでに累積されるようにできているという点で,非常につごうがよい。
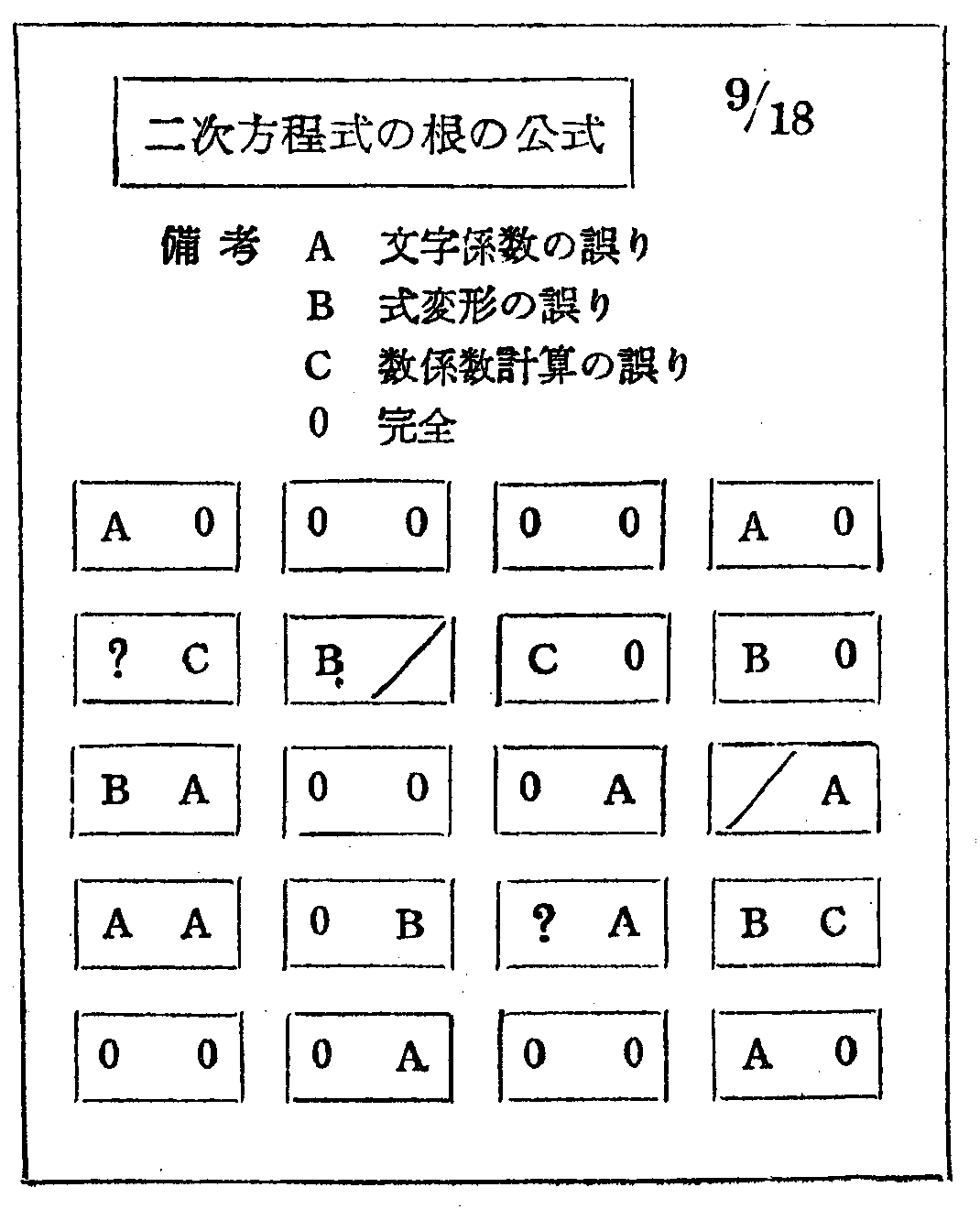
〔例2.〕 次に示したのは,各時間の記緑をとるのに,生徒の座席表をプリントしておいて,それにメモしていく方法をとったものである。
次の図は,この方法で,二次方程式の根の公式を指導する際にとった,記録の一例を示したものである。
これは,授業中に,目に写ったままを記入したり,授業が終った後に,授業中の状況を思い起して記入する場合に,いちいち名前と照合しなくてもよいから,つごうがよい。
〔例3.〕 単元によって学習指導をした場合に,その成果を評価するための記録のしかたの例として,第Ⅵ章の221ページにあげたような方法がある。
これも,記録の方法としては,よい方法である。
以上,評価の方法や手順として,上に述べたことは,評価を的確に,しかもそれを手ぎわよくするという見地からくふうしたもののいくつかをあげたものである。したがって,これらを参考にして評価をしようとする場合には,それぞれが,どんな意味でくふうされているものかを考えることが必要である。それを考えないで,形だけをまねるようなことは意味がない。また,実際には,これよりも進んだくふうをしている人も多いと思われる。とにかく,各自でこのようなくふうをして,少しでも,評価が能率よくできるようにしていくことが,重要である。