§１．各科目の性格
 

どうして，高等学校で数学科が選択必修になっているか。

　高等学校の目標として，個性の伸長，社会人の育成，職業的資質の啓培の三つの面があげられている。この三つの面から考えてみると，高等学校では，中学校の数学科の指導を受けついで，これをさらに発展させていくことが，どの生徒にも必要であることは，論をまたないところであろう。しかしながら，一面，生徒はこの時期になれば，自分の将来の進路に対して，しだいにはっきりした考えをもつようになり，この進路に応じて，必要とする数学の方向や程度がいろいろ違ってくると予想される。

　それゆえ，高等学校の数学科では，いくつかの科目を設け，そのうちの少なくともひとつを必修にすることをたてまえとしている。
 

科目を分けるにあたって，どのようなことを考慮しなければならないか。

１．まず第一に考えなければならないことは，高等学校の教育課程構成上からの制約である。すなわち，現在の高等学校は大教科主義をとり，１年間にあるまとまった学習をして，単位をとっていくことをたてまえとしている。

２．次に考えねばならぬことは，生徒の内面的な発達である。これについては，次の２点があげられる。

(ａ)　数学に対する理解が中学校の学習によって深まるにつれて，数学としてとりあげられるものに，いろいろ違った面のあることがわかり，生徒の個性に応じて，興味や関心を覚える面が違ってくる。

(ｂ)　生徒はしだいに論理的に考えることができるようになり，この違った面に対しても，数学的な見方から区別をつけることができるようになる。

３．職業的な必要から考えて，一般教養としての面を強調した科目と，職業的な資質としての能力をも強調した科目とが必要である。

１．科目のまとまりをつけていく観点として，大ざっぱに考えて，次のふたとおりの性格を考えている。

　その一は，将来それほど数学を必要としない生徒に対して，一般的教養という立て前から，中学校の学習を発展させたものである。一般数学がこれにあたる。その二は，将来数学を必要とする生徒，あるいは，数学をもっと深く学習したい生徒に対し，その必要と関心に基いて分けた科目である。解析Ⅰ，解析Ⅱ，幾何がこれに相当する。

２．解析Ⅰ・解析Ⅱと幾何とに分ける観点としては，次のような考え方をとっている。すなわち，数学の分野として，生徒に考えられる分け方は，数量関係を問題としていく面と，図形的な関係を問題としていく面とである。生徒の関心は，主としてこのような面に分化してくる。解析Ⅰ，解析Ⅱは前者にあたり，幾何は後者にあたる。

３．数量的な関係を問題にしていく面では，その第一の段階として，函数を大局的にそのグラフや式の形によってとらえ，これに必要な計算を行っていくものと，このような見方をさらに発展させ，いろいろな問題に応用して規則性をとらえたり，函数そのものについて微小変化や極限を考えてさらにつきこんだ見方をしたりしていくものとが考えられる。この前者にあたるものが解析Ⅰであり，後者は解析Ⅱにあたる。したがって，解析Ⅱは解析Ⅰに引続いて学習されるべきものである。

４．図形的な関係を問題にしていくのは，幾何である。幾何では，図形的な関係を問題として，これに対する方法として論証的な見方や解析的な見方を発展させる。

５．上のように分けた場合，いちばん気をつけなければならないことは，次のことである。これらの科目は，いずれも数学的な考え方を学ぶ点では共通なものであって，その問題の所在や必要な程度によってのみ分けたものである。したがって，その目標や指導内容においては，たぶんに共通なものを含んでいるようにしなければならない。

§２．一般数学の一般目標と指導内容

１．数学の応用の広いことや，数学が文明の進歩の上に果している役割について理解し，数学に対する関心を深める。

２．日常生活で当面する実務や消費生活について，数量的な観察をして問題を構成する能力や，その解決に必要な数学的な知識技能を身につけるとともに，それらを用いる習慣を養う。

３．いろいろな関係を簡単めいりょうに表わすものとして，また，問題解決にあたっての有力な道具として，数学を理解し，数学的な記号や操作を用いる能力を養う。

４．簡単な図形の性質を知り，それらが実際的な問題の解決にあたって果している役割を理解し，これを用いて，新しい問題を解決していく能力を養う。

５．論理的な考え方の本質と必要とを理解し，筋道を立てて，論理的に考えていく習慣を養う。

６．数量的な処理をしていくときに，数値の正しさや，それに対する制限を考えていく習慣を養う。特に，統計的な資料のとり方，整理のしかた，解釈のしかたについての理解を深めるとともに，物事を誤りなくとらえたり，正しく伝えたりする能力と，統計的な考え方を社会生活で正しく用いる態度とを養う。

１．指導内容を，生活経験によってあげたのは，中学校の場合と同じ趣旨によっている。これについては，37ページを参照せられたい。

２．ここにあげてあるのは，指導内容の一例であって，生徒の能力や必要に応じて，ある事がらを省くとか，つけ加えるとかなどして指導してよいことは，いうまでもない。

３．指導にあたっては，これらの生活経験を豊かに含んだ生徒の問題をとりあげ，この問題の解決をとおして，これらの数学的な内容を身につけていくことができるようにすることが望ましい。これについては，第Ⅵ章を参照せられたい。

生　活　経　験	理　解　お　よ　び　能　力	用　　語
①自然現象や社会現象を理解したり，これについての問題を解くために，公式やグラフを用いる。 (例) 　○落体の運動を示すために，その位置とかかった時間との関係を式に書いたり，グラフにかいたりする。 　○物価指数などの計算のしかたを示す式を調べて，なぜそのように，計算するのかを研究する。	○一次函数や簡単な二次函数のグラフをかいたり，これを用いたりする。 ○公式の式の形から，比例関係や反比例関係を見いだす。 ○一般角に対する三角函数の定義を知り，また，三角函数や，そのグラフを用いる。 ○いろいろなグラフの特徴を知り，これを用いる。 ○変化率の意味を理解する。	○函数 ○変化率 ○２乗に比例(反比例)， ○一般角 ○周期 ○振幅
②日常生活に関係して起る問題を，方程式を用いて解く。 (例) 　○単利などについての計算をするのに方程式を用いる。	○未知の量をｘやｙによって表わし，条件を方程式の形にまとめる。 ○一般の一元一次方程式を解く。 ○二元一次連立方程式を解く。	○元，一次，二次 ○消去
③図形の取扱に慣れ，簡単な図形の性質を知る。 (例) 　○測量や装飾をするのに，三角形や円などの簡単な性質を用いる。 　○日常に用いている器具の形に回転体・対称形・平行線などが用いられているわけを研究する。 　○工業などで，投影図がどんな役割を果しているかを研究する。	○公理・定義および定理・証明の意味を明らかにする。 ○平行線の定義やその性質を理解する。 ○合同相似の条件を理解し，これを用いて図形をかいたり，図形の性質を明らかにしたりする。 ○対称形の概念や，その基本的な性質を理解し，これを用いる。 ○回転体の概念や，その基本的な性質を理解し，これを用いる。	○公理，定義 ○定理，証明 ○同位角
④測定値について，その代表値の信頼度やその制限の意味を理解し，また，これを計算に用いる。 (例) 　○具体的な物の面積・体積などを計算するのに，測定値の平均や，その制限を用いる。 　○面積・体積などの概略の大きさを推定するのに概算を用いる。	○相加平均の意味を理解する。 ○正しさ・くわしさの概念を理解し，これを用いる。 ○測定値の正しさを標準偏差によって示す。 ○計算尺を用いて，測定値についての計算をする。 ○概算をする。	○相加平均 ○代表値
⑤社会現象や自然現象について確からしさの意味を理解し，これに関する問題を解く。 (例) 　○保険などに用いられる死亡率の意味を理解する。 　○あたりくじを引くのは，くじを引く順序に関係あるかどうかを調べる。	○確率の意味を理解する。 ○独立事象や，排反事象の意味を理解する。 ○確率の加法法則・乗法法則の意味を理解し，また，これを用いる。 ○場合の数を残りなく，また，重複なく数える。	○確率(数学的，統計的) ○独立，排反 ○加法法則，乗法法則 ○期待値 ○順列，組合せ
⑥社会現象について，その実態を理解したり，将来を予測したりするのに，統計的な資料を用いる。 (例) 　○身長が大きいほうか小さいほうかを判断するために，その年齢における身長の平均を調べる。 　○社会のいろいろな問題についての世論調査を研究して，その価値と限界とを調べる。	○資料は，どんな性格のものでなければならないかを知る。 ○全体調査・一部調査などの資料の集め方のあることを理解する。 ○標準偏差の意味を知り，これを計算する。 ○表によって，簡単な相関関係を知る。 ○いろいろなグラフの用途を知る。	○モード ○中央値 ○標準偏差 ○相関関係 ○カルトグラム
⑦経済や金融に関して用いられているいろいろな比率の意味を理解し，これに関する問題を解く。 (例) 　○将来の職業生活に役だてるため，金融機関の利用法や商販引の方法を研究する。 　○物価が何によって変動するかを明らかにし，家計や賃金の問題に対する理解を深めるため，統計資料として指数を用いる。 　○家族の生活を保証する一つの方法として，保険や貯蓄の意義を研究する。 　○税金を完納するため，一年の税額を見積り，貯蓄の計画をたてる。	○歩合・百分率・指数の意味を理解し，これを有効に用いる。 ○加重平均などの考えをもとにして，総合指数の意味を理解する。 ○歩合・百分率の三つの用法についての計算をする。 ○小切手・かわせ・手形などの意味を知り，これについての計算をする。 ○保険や貯蓄の意味を知り，これについての計算をする。 ○複利か長期の融資や年金などの計算に用いられているわけを知り，表を用いて，これに関する計算をする。 ○利まわりについての計算をする。 ○数列の意味を理解する。 ○等比数列の和を計算する。 ○対数表を用いて計算する。	○年金，年賦金 ○数列，等比数列 ○対数 ○加重平均 ○相乗平均
⑧金銭に関する計画や記録の際にバランスを考えることが重要であることを理解し，これに関する計算をする。 (例) 　○商店や農場の経営を合理化するため，簡単な簿記や青色申告の書き方を研究する。 　○国の予算について研究する。 　○生徒会の予算を編成する。	○収支や損益の計算に必要な量に正負の符号を考え，その和がいつも０であるとみなすことの意味を理解する。 ○簡単な簿記をつける。 ○予算・決算・家計簿・バランスシートなどの見方やその意味を知る。
⑨数学が文明の進歩の上に果している役割について理解する。 (例) 　○幾何学によって，測量や地図製作がどんなに進歩したかを研究する。 　○自然科学の進歩に数学がどのように貢献しているかを研究する。 　○将来の危険や不安に詞なえる備えるのに，数学がどのように用いられるかを研究する。 　○社会の秩序を維持し，公正をはかるために，数学がどのように用いられているかを研究する。	○関係を式やグラフで表わすことの意義を知る。 ○確率や統計を用いることの意義を知る。 ○図形による表現の意義を知る。 ○図形についての研究の意義を知る。 ○数計算の方法の進歩が，いろいろなことについての労力を節約してきていることを知る。

§３．解折Ⅰの一般目標と指導内容

１．函数や式の概念を理解し，その有用なことを知る。

２．簡単な函数の性質を理解し，これを実際的な問題の解決に有効に用いる能力を伸ばす。

３．函数や式についての用語や記号と，その正しい使い方を理解する。

４．日常生活においても，数量的な関係について，簡潔な表現を用いる態度を養う。

５．グラフによる表現が，数量的な傾向や法則を具体的に明らかに示すものであることを理解し，これを問題解決に生かす能力を伸ばす。

６．式による表現が，数量的な傾向や法則を演算に適するようにまとめたものであることを理解し，これを問題解決に生かす能力を伸ばす。

７．グラフや式のよさを生かして，これを適切に用いる態度を養う。

８．数を拡張しても，これを一般的に取り扱うことができることを理解する。

９．数や式をうまく取り扱う方法をくふうする能力を養う。

1O．数や式やグラフをうまく用いて，思考を単純にしたり，思考に要する労力を節約したりする態度を養う。

ll．数学が文明の進歩の上に果している役割を理解し，数学に対する関心を深める。

１．次にあげたのは，解析Ⅰのおもな指導内容を，その配列の一例を用いて示したものである。この配列は，指導内容の配列の一例であって，ほかの見地から内容を別に組織したり，生徒の能力や必要に応じて，ある事がらを省くとかつけ加えるとかなどして指導してよいことは，いうまでもない。

２．この配列は，中学校からの函数的な見方を伸ばすとともに，しだいに代数的な取扱方を取り入れていき，解析Ⅰの目標を達成しようとする考え方でつくられたものである。すなわち，次のような流れになっている。

　数量的な関係を明確に記述し，これを能率よく処理しようとして代数的な方法をまず取り入れる。よりいっそう複雑な数量的な関係の処理が必要となるにつれて，しだいに進んだ代数的な方法をとりいれ，その内容を展開していく。代数的な取扱が相当に進んだところでこれをまとめる。また，さらに数計算の能率をいっそうあげることを考えて，対数を取り入れる。

３．指導されるときには，生徒や学校の設備・教員組織等に応じて，適切な方法を用いていただきたい。すでに，「中学校・高等学校における一般学習指導法」が刊行されている。また，「数学科の学習指導法」が現在執筆されつつある。これらの書物を参考にして，その一般な方法を実際にうまく適用して，指導の効果をあげるように，指導の方法をくふうしていただきたい。

Ⅰ．中学校の数学の復習

Ａ．目標　中学校での重要な理解事項と技能とをまとめ，今後の学習の準備をする。

Ｂ．内容

１．文字や記号を用いて数量的な関係を表わすこと。

２．正の数・負の数を用いること。

３．解析Ⅰの学習に必要な三角形の合同・相似の条件，三平方の定理，三角比等の幾何学的事項をまとめこと。

Ⅱ．比例および一次の関係を用いること

Ａ．目標
１．函数的な関係を見いだす能力をうる。

２．式やグラフによる関係の表わし方を理解し，そのおのおのの特質を知る。

３．比例や一次の関係で表わされた公式を理解し，これを有効に用いる能力をうる。

４．一次方程式や一次不等式の意味を理解し，これを解く技能を伸ばす。

Ｂ．内容
１．一次の比例(ｙ＝ａｘ)
ａ．日常生活や科学の研究に現れてくる比例の関係を見いだし，式やグラフに表わすこと。

ｂ．比例関係を表わす式や，グラフの共通な性質や，式の係数とグラフの形との関係を見いだし，これを用いること。

２．一次の関係
ａ．日常生活や科学の研究に現れてくる一次の関係を見いだし，式やグラフに表わすこと。

ｂ．一次の関係を表わす式や，グラブの共通な性質や，式の係数とグラフの形との関係を見いだし，これを用いること。

ｃ．一次の関係と比例の関係との異同を明らかにすること。

３．一次方程式・一次不等式
ａ．具体的な場合について，問題に示された条件を方程式や不等式の形に表わすこと。

ｂ．一次方程式・一次不等式の意味を明らかにし，その一般的な解法の原理を見いだして，これを用いて手ぎわよく方程式・不等式を解くこと。

Ｃ．用語
一次式，係数，定数項，こうばい，同位角，比例定数，載片，一次方程式，一次不等式，移項，平行移動。

Ⅲ．函数の概念を用いること

Ａ．目標
１．函数の概念を理解し，これを用いる能力をうる。および，その有用なことを知る。

２．式やグラフで函数関係を表わすことの意味を理解し，これを用いる能力をうる。および，その有用なことを知る。

３．一般の比例，二次，および，三角函数の性質を理解し，これを用いる能力をうる。

Ｂ．内容
１．一般の比例関係
ａ．日常生活，科学の研究，図形についての数量関係に現れてくる公式について，一般的な比例関係(反比例，２乗に比例，２乗に反比例，平方根に比例など)を見いだし，その式やグラフの特徴を理解すること。

ｂ．上の場合における一次の比例関係との異同を明らかにすること。

ｃ．変数(独立・従属)，函数関係，変域の概念を一般化すること。および式を用いることによって，変数や変数の関係のしかたが的確に表わされることを明らかにすること。

２．二つ以上の独立変数をもつ函数関係
ａ．日常生活，科学の研究，図形についての数量関係に現れてくる公式について，二つ以上の独立変数をもつ比例の関係を見いだしたり，これを用いたりすること。

ｂ．簡単な公式について，そのうちのひとつの従属変数について，方程式の考えを用いて，公式を変換すること。

３．二次式で表わされる函数関係
ａ．二次式で表わされるような函数関係を具体的な場面に見いだすこと。

ｂ．二次式のグラフの形を研究すること。および，グラフを用いて問題を解決すること。

ｃ．二次式の変化を一次式や比例の変化と比較して，その特徴を知ること。

ｄ．グラフを利用して，二次方程式や二次の不等式で表わされる問題を解決すること。および，グラフがいろいろな問題の解決に有用であることを明らかにすること。

４．周期的な函数関係
ａ．日常生活や科学の研究に現れてくる周期的な函数関係を見いだし，これをグラフに表わすこと。

ｂ．角を一般角にまで拡張し，鋭角での三角比についての関係がそのまま保たれるように，一般角の三角函数をつくること。

ｃ．三角函数の周期的な性質や，その他の簡単な性質を研究すること。

Ｃ．用語
函数，変数，変域，２乗に(３乗に，平方根に)比例，２乗に(３乗に，平方根に)反比例，複比例，放物線，直角双曲線，実験式，上に凸，下に凸，二次式，一次函数，二次函数，最大，最小，一般角，動径，象限，周期，周期函数，正弦曲線，正弦，余弦，正接，余接，余角，補角，sin，cos，tan，cot，ｆ(　)

Ⅳ．数や式についての計算をすること

Ａ．目標
１．式が数と同じように取り扱えることを理解する。

２．数や式の計算のもとになっている法則や計算の意味を理解し，これを用いる能力をうる。

３．式についての計算を正しく手ぎわよくする能力を伸ばす。

Ｂ．内容
１．数の計算の基本的法則
ａ．具体的な整数の計算をとおして，その計算がどんな基本的法則をもとにしているかを明らかにすること。

ｂ．基本的法則をうまく用いた能率的な数計算のくふうをすること。

ｃ．平方根数の計算についての基本的な関係を明らかにすること。および，これを用いること。

２．式の四則の意味，およびその基本的法則
ａ．具体的な場合について，数と式とを対比して式の計算の基本的法則が数と同じであることを明らかにすること。

ｂ．基本的法則を用いて式を簡単にすること。

ｃ．整式についての四則計算の方法を，十進数の計算と対比して，数と同じように簡潔にできるようにくふうし，これを用いること。

ｄ．整数についての最大公約数・最小公倍数の意味を復習し，これと比べて，整式についての最大公約数・最小公倍数の意味を明らかにすること。およびこれを用いること。

ｅ．簡単な分数式の四則や簡約をすること。

３．基本的な整式の積の公式
ａ．因数分解の意味を明らかにすること。および簡単な場合

　(ａ²−ｂ²，二次三項式，ａ^３±ｂ^３の公式を適用する程度)についての因数分解をすること。

ｂ．因数分解によって整式の最大公約数・最小公倍数を求めること。

Ｃ．用語
整式，項，多項式，単項式，交換法則，結合法則，分配法則，因数，因数分解，二次三項式，展開，通分，約分，既約分数，同類項，簡約，正項，負項，整除

Ⅴ．連立一次方程式を用いること

Ａ．目標
１．問題の条件を方程式や不等式で表わすことのよさと制約とを理解する。

２．未知数を適当にとって，条件を簡潔にわかりよく表わす能力をうる。

３．方程式によって問題を解決していくときの原則を理解し，これをじょうずに用いる技能を伸ばす。

Ｂ．内容
１．文章で表わされた条件を式に書くこと。
ａ．一つの文字を使って具体的な条件を式に書くこと。

ｂ．やや複維な一元一次方程式や不等式を解くこと。

ｃ．具体的な問題について，二つ以上の文字を使って条件を簡潔な式に書くこと。

２．連立一次方程式
ａ．二元一次方程式で示された関係をグラフに表わすこと。

ｂ．連立方程式の意味，および二つの未知数を用いる場合とひとつしか用いない場合とを比較したときの，連立方程式の有用性を明らかにすること。

ｃ．未知数を消去することの意味およびその方法を明らかにすること。およびこれによって方程式を解くこと。

３．方程式・不等式を用いて問題を解くこと。
ａ．具体的な問題について，その条件を分析して，方程式・不等式にのせること。

ｂ．連立二元一次方程式を用いて問題を解くこと。

Ｃ．用語
連立方程式，元，消去，代入法，加減法，不能，不定

Ⅵ．二次式や分数式を用いること

Ａ．目標
１．式・方程式・不等式を，目的に応じてじょうずに変形する能力をうる。

２．方程式・不等式による問題解決のよさを知り，二次方程式を用いて問題を解決する能力を伸ばす。

３．根の公式・判別式などの式を用いることのよさを知る。

４．数の取扱がより一般的にできるように，数の概念が拡張されていることを理解する。

Ｂ．内容
１．二次函数および式の変形
ａ．具体的な問題について二次式を平方完成の形にし，式の値の変化を見やすくして研究すること。

ｂ．一般の二次式のグラフの形と式の係数との間の関係を明らかにすること。

ｃ．二次式で表わされる函数関係を用いて，最大・最小に関する具体的な問題を解決すること。

２．二次方程式
ａ．二次方程式を式の変形(平方完成・因数分解)や根の公式を用いて解くこと。

ｂ．二次方程式を用いて，具体的な問題を解決すること。

ｃ．二次不等式の解と二次方程式の根との間の関係を明らかにし，これによって二次不等式をできるだけ簡潔に解くこと。

ｄ．方程式の根を利用して，式を因数分解すること。

ｅ．二次方程式の根と係数の関係や判別式を利用すること，およびそのよさを明らかにすること。

３．等式・不等式の基本的性質
ａ．これまでの具体的な方程式の解法の方針をまとめること，および方程式の同値関係を明らかにすること。

ｂ．二次方程式に簡単に帰着できる分数方程式・無理方程式を解くこと。およびそのときに根の検討が必要であることを理解すること。

ｃ．基本的な不等式，および不等式の同値関係を研究すること。

ｄ．比例式の性質を明らかにし，これを用いること。

４．数の概念を拡張する原理
ａ．有理数・実数・複素数というように，同じ原理に基いて数の概念が拡張されていることを明らかにすること。

ｂ．複素数も実数と同じように四則計算ができることを理解すること。

Ｃ．用語
二次方程式，完全平方，等根，実根，虚根，判別式，分数方程式，無理方程式，同値，必要条件，十分条件，逆，二次不等式，絶対不等式，｜ａ｜，有理数，無理数，実数，虚数，虚数単位，ⅰ，複素数，共軛

Ⅶ．図形を式を用いて研究すること

Ａ．目標
１．座標をなかだちにすると，方程式と図形とが結びつくことを理解する。

２．図形の基本的性質や，図形が点の運動によってできたものとみられることを理解する。

３．式を目的に応じて自由に使いこなす能力を伸ばす。

Ｂ．内容
１．図形に関する問題を方程式を用いて解くこと。
ａ．三角形の相似の条件や，三平方の定理を用いて，図形に関する問題を解くこと。

ｂ．三角形の内角の和が180゜であることを知り，これを用いること。

２．座標を用いて図形を表わすこと。
ａ．座標によって，二点間の距離や，二点を結ぶ線分を定比に分つ点を求めること。

ｂ．二元一次方程式の一般の形と直線の位置との間の関係を明らかにすること。

ｃ．円・楕円・双曲線・放物線の標準型の方程式を理解すること，および方程式の係数と図形の形との関係を研究し，その概形を知ること。

ｄ．二次と一次との連立方程式を解くこと。およびこれを用いて問題を解決すること。

Ｃ．用語
直線の方程式，円・楕円・双曲線・放物線の方程式，点対称，線対称，長軸，短軸，漸近線

Ⅷ．数計算を能率よくすること

Ａ．目標
１．対数を用いて，能率的に数の計算をする能力をうる。

２．対数がどんな原理に基いてつくられたかを理解する。

３．いろいろな計算の能率化のくふうのよさを知る。

Ｂ．内容
１．指数の拡張，および対数の意味
ａ．具体的な数の計算をもとにして，指数の規約が指数法則をいつもなりたたせるように決めてあることを理解する。

ｂ．指数法則を用いて，計算を能率的にするようにくふうすること。

ｃ．対数の意味と対数計算の原理を明らかにすること。およびその有用なことを知ること。

２．対数計算
ａ．常用対数表の用い方を理解すること。および，10を底にとることが便利であることを明らかにすること。

ｂ．対数を用いて，日常生活や科学の研究に必要な諸計算を能率的にすること。

ｃ．計算尺の原理を明らかにし，その使い方に慣れること。

３．計算図表その他のくふう。
ａ．対数目盛を用いた方眼紙によって，函数関係を単純化して表わすこと。

ｂ．簡単な計算図表について，その原理や使用法を明らかにすること。

Ｃ．用語
累乗，指数，累乗根，指数法則，対数，log，対数の底，真数，常用対数，比例部分，指標，仮数，全対数方限紙，半対数方眼紙，計算図表
　

注　高等学校数学科の用語については，文部省学術奨励委員会学術用語分科審議会の決定したものを参考とし，原則としてはこれを用いることにして，教育的な見地からその採否を定める予定であったが，現在まで同審議会の正式の決定をみないので，ここでは従来の用語をそのまゝ用いることにしてある。

§４．解析Ⅱの一般目標と指導内容

１．日常生活や科学の研究における問題について，数量を用いて客観的にしかも能率的に判断する能力を養う。

２．式や記号を用いて思考を単純にしたり，思考に要する労力を節約したりする能力と態度とを養う。

３．日常生活や科学の研究において，ものをうまく整理して配列したり，その配列の規則を見いだしたりする能力と，物事の規則をうまくとらえて処理する能力と態度とを養う。

４．近似や極限の概念を理解し，これをいろいろな分野における問題の解決に適用する能力を養う。

５．数値の正しさやそれに対する制限を考えて数量を処理していく能力を養う。

６．上の能力を計量に生かし，能率的にしかも手ぎわよく処理する態度を養う。

７．統計的な資料のとり方，整理のしかたを，解釈のしかたを理解し，物事を誤りなくとらえたり，また正しく伝えたりする能力を養う。

８．統計的な考え方を，社会生活において正しく用いる態度を養う。

９．数学が文明の進歩の上に果している役割を理解し，数学に対する関心を深める。

１．次にあげたのは，解析Ⅱのおもな指導内容を，その配列の一例を用いて示したものである。この配列は，指導内容の配列の一つの例であって，他の見地から内容を別に組織したり，生徒の能力や必要に応じて，ある内容を省くとか，つけ加えるとかなどして指導してよいことは，いうまでもない。

２．この配列は，解析Ⅰで発展した解析的な見方を，いろいろな方面に適用するとともに，しだいに確率や極限の見方を取り入れていって，解析Ⅱの目標を達成しようとする考え方からつくられたものである。すなわち，次のような流れになっている。

　まず，代数的な見方を個数の処理や確率的事象の研究に応用して，確率その他の考え方を発展させ，次いで，函数的に見られる事象に解析的な方法を応用しつつ，しだいに極限による考え方を発展させ，これを計量に応用する。最後に，三角函数による見方をさらに発展させて，計量をある意味での完成にまで高めていく。

３．指導するときには生徒や学校の設備，教員組織等に応じて，適切な方法を用いていただきたい。すでに「中学校・高等学校における一般学習指導法」が刊行されている。また「数学科の学習指導法」が現在執筆されつつある。これらの書物を参考にして，その一般的な方法を，実際にうまく適用して，いっそう指導の効果をあげるように，指導の方法をくふうしていただきたい。

Ⅰ．確率を理解し用いること

Ａ．目標
１．順列や組合せの考えを用いて，場合の数をじょうずに計算する能力を伸ばす。

２．確率や期待値の概念を理解し，そのよさを知る。

３．確率や期待値を用いて，客観的に確からしさについての判断をする能力をうる。

４．確率の大数法則の意味を理解し，統計を正しく用いる態度を伸ばす。

Ｂ．内容
１．順列や組合せ
ａ．具体的な場面において，複雑な場合の数をどんな方針で分類し整理したら，数えやすくなるかを明らかにすること。

ｂ．複雑な場合の数の例として，順列や組合せの考えを見いだし，これについて上の方針で公式を導くこと。

ｃ．順列や組合せの考えを用いて，いろいろな具体的な問題を解決すること。およびこれらの考えが問題の解決を能率よくしていることを知ること。

ｄ．二項式の累乗の展開を計算すること。およびその係数の間の関係を見いだすこと。

ｅ．指数が整数の場合の二項定理を明らかにすること。およびこれをいろいろな計算に利用すること。

２．確率および期待値の意味
ａ．死亡率とか男女の比とかいうような統計的な割合が，多数の対象について調べたときには，ほとんど一定とみられる事実を知ること。およびこの事実の将来の計画等に対する有用性を知ること。

ｂ．さいころやくじびき等の実例によって，数学的確率と，そのことを多数回試みたときの統計的割合とが，ほぼ等しいことを認めること。および，確率の概念を明らかにすること。

ｃ．起りうるあらゆる場合の数を数えて，確率を計算し，用いること。

ｄ．くじやその他の実例によって，数学的期待値の意味を明らかにすること。

ｅ．確率を用いるときの注意(確率が多数回くり返して起りうることにのみ適用されること)や，これが実際的な広い応用をもっていることを知ること。確率が０または１であることの数学的な場合および統計的な場合の意味を明らかにすること。

３．確率についての計算
ａ．死亡率やさいころのような具体的な例によって，すでにわかっている確率をもとにして，より複雑な確率を計算によって求めること。

ｂ．排反事象や独立事象の概念の意味を明らかにすること。および，このような概念を用いることによって，確率の計算の見とおしがよくなるという利点を知ること。

ｃ．確率の乗法定理や加法定理を用いて，じょうずに確率を計算すること。

ｄ．具体的な場合について，一定の確率をもった事象を何回かくり返した場合の，その事象の現れる回数を計算し，これに基いて，二項分布の一般的な特徴をまとめること。

ｅ．上の例について，期待値を求めたり，期待値に近いをうる確率を計算したりして，大数法則の理解を深めること。および期待値や確率の概念を用いること。

Ｃ．用語
順列，組合せ，_nＰ_r，_nＣ_r，階乗，nl，二項定理，二項係数，確率(数学的，統計的)，排反事象，独立事象，加法定理，乗法定理，期待値，二項分布，大数法則

Ⅱ．資料を整理し，解釈すること

Ａ．目標
１．資料を整理して，その中心的傾向を，グラフや表を用いたり，代表値を用いたりして表わす能力を伸ばす。

２．平均値の確からしさが標準偏差で表わされることを理解する。

３．資料の信頼性を見分ける観点を理解する。

４．統計的な方法が有用であることを知る。

Ｂ．内容
１．資料の表やグラフによる整理
ａ．学校や近くの社会で調べた資料を，項目別や階級別に整理して，その度数を数えることによって，全体としての様子を明らかにすること。

ｂ．上の例について，度数分布表や度数分布グラフの使い方を理解する。

ｃ．階級の幅を変えて資料を整理すると，度数分布グラフがどのように変るかを実例について研究すること。

ｄ．具体的な資料について，いろいろな型の分布の実例を知ること。およびその分布の型が表わす意味を研究すること。

ｅ．体重と身長等の具体的な例について，二つの数量の間の関係を調べる方法として，相関表や相関グラフを用いること。

２．資料の特徴を表わす数値
ａ．具体的な資料について，平均値やモード，中央値等の代表値を求めること。およびそのおのおのの長所を知ること。

ｂ．平均値の簡便な計算法をくふうして，具体的な場合にこの計算法を用いること。

ｃ．具体的な資料について，平均値に対する散布度を表わすものとしての標準偏差の意味を明らかにし，これを計算すること。具体的ないくつかの資料について，平均からの差が標準偏差の何倍かを越えない値の割合を実際に計算すること。および標準偏差と平均値との関係を理解すること。

ｄ．標準偏差の簡便な計算法をくふうして，具体的な場合に用いること。

ｅ．資料をグラフや表に表わすことと，平均値と標準偏差で表わすこととを比較して，そのおのおのの特徴を知ること。

３．資料を集めたり，引用したりするときの注意
ａ．統計的な法則の意昧やこれに基いて個々の事象を判断するときに注意すべき事項を研究すること。

ｂ．統計資料がどんな性格をもてば信頼できるかを明らかにすること。

ｃ．一部調査による平均値の確からしさを，身近な実例を用いて研究すること。

ｄ．一部調査で全体を代表させるときの注意，および実際に用いられている一部調査の方法を知ること。

Ｃ．用語
度数，度数分布，階級，変量，範囲，偏差，標準偏差，相関，相関表，代表値，相加平均，加重平均，モード，中央値，一部調査

Ⅲ．数列や級数を用いること

Ａ．目標
１．数列を構成している一般的な法則を見いだす能力をうること。

２．式を用いて一般的な関係を表わす能力を伸ばすこと。

３．数列について，極限の概念を理解する。

４．式を用いることが有用であることを知る。

Ｂ．内容
１．数列の規則
ａ．日常生活その他の具体的な場面に現れてくる数列や，半具体的に数で与えられた数列について，相隣る二項の差や比によって，その一般的な法則を見いだすこと。

ｂ．具体的な，または半具体的な数列について，これを自然数列と対応させ，一般項の形を求めること。およびこれを用いて未知の項を計算すること。

ｃ．等差数列・等比数列の意味とその一般の形を明らかにすること。

２．数列の和
ａ．具体的に数で与えられた等差数列について，その和を簡便に求める方法をくふうすること。

ｂ．等差数列の和の公式をつくり，これを用いていろいろな問題を解決すること。

ｃ．具体的に数で与えられた等比数列について，その和を簡便に求める方法をくふうすること。

ｄ．等比数列の和の公式をつくり，これを用いて金融その他に現われる具体的な問題を解決すること。

ｅ．その他の簡単な数列の和の公式をつくり，これを用いること。

ｆ．具体的な場合について，数学的帰納法を用いて証明を行うこと。

３．数列の極限
ａ．具体的に数で与えられた等差数列や等比数列について，その項数がしだいに大きくなっていったときに，その値がどんなに変化していくかを研究すること。

ｂ．収斂・発散・振動の意味を理解すること。および等比数列が収斂するための条件を明らかにすること。

ｃ．年金その他の例によって，無限等比級数の意味を明らかにし，その極限の値を求めること。

ｄ．その他数列の極限とみられるいろいろな量を研究し，極限による考え方の有用なことを知ること。

ｅ．循環小数が有理数を表わすことを明らかにすること。

Ｃ．用語
数列，等差数列，等比数列，公差，公比，項，第ｎ項，一般項，ａ_n，Σ，無限等比級数，収斂，発散，振動，極限，循環，小数(純〜，混〜)，無限小数，数学的帰納法

Ⅳ．函数の概念を拡張し，完成すること

Ａ．目標
１．函数の一般的な概念についての理解を広げる。

２．初等的な函数の性質を用いる能力を伸ばす。

３．函数の連続性についての理解をうる。

４．函数の慨念が有用であることを知る。

Ｂ．内容
１．函数の概念
ａ．日常生活の問題に関係して経験するいろいろな函数関係をグラフや式に表わして調べること。およびこれらの函数関係は，必ずしも単純な式で表わせるとは限らないことを認めること。

ｂ．函数の意味を明らかにすること。およびこれを統計的な研究によって得られる相関関係と比較すること。

２．解析Ⅰで学習した初等的な函数の性質のまとめと発展
ａ．一次函数は，単調に増大または減少すること。

ｂ．比例関係は，対数目盛を用いると，直線で表わされること。

ｃ．二次函数は，最大値または最小値を一つだけ持つこと。および独立変数が増加するときは，初め単調に増加し，次に単調に減少するか，あるいは，初め単調に減少し，次に単調に増加するかいずれかであること。

ｄ．三角函数は周期的変化をすること。

・　指数函数もまた単調に変化する函数であり，複利の計算など，日常の場面によく現れるものであること。

ｆ．対数函数もまた単調に変化することを認めること。指数函数と逆の関係にあることを明らかにすること。

ｇ．3ｘ＋5ｙ＝５やｘ²＋ｙ²＝８などのように，陰函数の形で表わされた函数関係を認めること。

・　函数の連続性
ａ．不連続点をもつ函数のあることを知ること。およびその点での函数値と，その点の近くでの函数値の極限との関係を明らかにすること(たとえば，郵便料金のグラフのように，ある種のグラフは飛躍している点をもっていること，および函数の値の極限は，独立変数をどちらから近づけるかによって，違った値をとることがあること。)

ｂ．函数値が無限大になることの意味を明らかにすること。(たとえば，反比例のグラフのように，ある種のグラフでは，上方または下方に無限に伸びているところがあること。および独立変数がある有限な値に近づくときに，函数の値が，絶対値において無限に大きくなることがあること。)

ｃ．函数の連続性の意味を明らかにすること。(独立変数のどんな値に対しても，ａやｂに述べられたような場合が起らないこと。)

ｄ．不等式を満足する点の範囲を求めること，たとえば，

　　ｙ−3ｘ−５＝０や3ｘ−2ｙ−８＝０などの一次函数のグラフの上側の点の座標は，それぞれ，ｙ−3ｘ−５＞０や3ｘ−2ｙ−８＜０なる不等式を満たし，下側の点の座標は，それぞれ，ｙ−3ｘ−５＜0，3ｘ−2ｙ−８＞０を満たすこと。および二次函数のグラフの上側，下側，あるいは

　　ｘ²＋ｙ²＝ｒ²のグラフの内側，外側などに対しても，同様な性質があることを認めること。

ｅ．連続な函数のグラフは，一般に平面を正の部分と負の部分とに分けること。およびそれをもとにして，不等式の解の存在する範囲を図示して，問題を解くこと。

Ｃ．用語
指数函数，対数函数，単調増大，単調減少，＋∞，−∞，無限大，連続，不連続。

Ⅴ．変化率を用いること

Ａ．目標
１．極限の考えによって，函数の変化率を明確に理解する。

２．変化率を，もとの函数の独立変数の函数とみて，これを用いる能力をうる。

３．導函数の有用性を知る。

Ｂ．内容
１．変化率
ａ．日常に用いられる平均変化率の意味を復習し，これによって，一次または二次の函数で表わされた数量関係を研究すること。

ｂ．具体的および半具体的な場合における函数の変化率を研究すること。(二次函数の場合には，平均変化率が一意に決まらないことを認め，速さやグラフの傾きなどの具体的な例をもとにして，平均変化率の極限としての変化率を理解すること。)

ｃ．いろいろな具体的および半具体的な整函数(二次式，三次式の程度)について，変化率を計算すること。また，これを用いて接線の方程式を求めること。

ｄ．接線の方向と，その接点の近くでの函数値の増加または減少の傾向との関係を明らかにすること。

２．導函数
ａ．具体的および半具体的な函数について，変化率が独立変数の値によって変ることを明らかにすること。およびこのことから導函数の概念を導くこと。

ｂ．二次式，三次式などについて導函数を計算すること。および，その符号の変化によって，函数値の増加・減少の傾向を研究すること。

ｃ．極大・極小の概念やその最大・最小との違いを明らかにすること。および具体的および半具体的な函数(二次式，三次式，および分母が一次式程度の分数式)について，導函数を求め，これを利用して，極大・極小の問題を解決すること。および導函数がこの種の問題の解決に有用であることを明らかにすること。

３．函数の近似

ａ．平方根表・対数表および三角函数表などについて，その一部を直線によって近似して，表の補間をすること。

ｂ.ｙ＝√ｘやｙ＝１／ｘなどのｘ＝１における接線によって，その近くの変化を近似できることを明らかにし，√１＋ｘ，１／１＋ｘなどに対する近似式を求めること。

ｃ．具体的な問題に上の近似式を利用して，その関係を簡潔化すること。

ｄ．相対誤差の意味を明らかにすること(簡単な式について，その独立変数の相対誤差と従属変数の相対誤差との関係を，微小変化の考えによって明らかにし，用いること。)

Ｃ．用語
平均変化率，変化率，増分，⊿ｘ，接線，lim(△ｘ→０)，速度，加速度，微係数，微分する，函導数，ｄｙ／ｄｘ，ｙ’，極大，極小，近似，近似式，相対誤差，絶対誤差

Ⅵ．計量において極限を用いること

Ａ．目標
１．極限によって，いろいろな量の大きさが明確にとらえられることを理解する。

２．積分の記号によって，極限としての量を簡単に表わすことができることを理解し，これらを用いる能力をうる。

３．積分が微分の逆の演算であることを理解し，これを用いる能力をうる。

４．近似の概念についての理解を深め，そのよさを知る。

Ｂ．内容
１．極限による量の大きさ
ａ．長さ・面積・体積などの量の大きさが，単位の長さ・正方形・立方体などをもとにしてできていることを復習し，その場合に，いつも極限の考えによって，大きさが表わされていることを理解すること。

ｂ．円を正多角形で近似して，その周や面積の極限としての円周の公式や面積の公式を導くこと。

ｃ．一次式や二次式で表わされる具体的および半具体的な数量関係について，区分求積法によって面積を求めたり，速さから道程を求めたりすること。これによって，極限の考えが有用であることを明らかにすること。

２．積分の記号と演算
ａ．上で求めた実例について，積分の記号を用いて，それらの量を求めた考え方とともに，その量の大きさを明確に表わすこと。

ｂ.ｙ＝ｘ，ｙ＝ｘ²などのグラフとｘ軸との間の面積を，ｘの函数として式に表わしてから微分してみると，もとの函数が得られることを知ること。

ｃ．上のことに基いて，微分と積分との関係を一般化すること。およびすでにわかっている定積分について，この関係を検証すること。

ｄ．上で求めた関係を用いて，いろいろな面積・体積，その他の実際問題を解決すること。

ｅ．具体的な函数のグラフや曲線について，これを適当に二次式で近似して積分し，シンプソンの法則をうること。およびシンプソンの法則を用いて，実際問題を解くこと。

Ｃ．用語
区分求積，定積分，積分，不定積分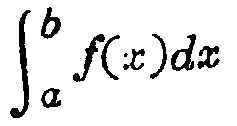　

Ⅶ．三角函数を用いること

Ａ．目標
１．三角函数の加法定理を理解し，これを用いる能力をうる。

２．角が小さい場合の正弦・正接の近似式を理解し，これを用いる能力をうる。

３．角の単位を知り，弧度法のよさを知る。

４．三角形の三角函数についての性質を知り，これを用いる能力を伸ばす。

５．加法定理が有用であることを知る。

Ｂ．内容
１．三角函数の加法定理
ａ．ｆ(ｘ)＝ｘ²，ｆ(ｘ)＝ｘ³，ｆ(ｘ)＝√ｘなどの例について，一次の比例以外の函数では，一般に，函数が加法的〔ｆ(ｘ＋ｙ)＝ｆ(ｘ)＋ｆ(ｙ)〕ではないことを明らかにする。

ｂ．三角函数もまた加法的でないことを，いろいろな場合について確かめ，sin(α＋β)，cos(α＋β)，tan(α＋β)と，α，βの正弦・余弦・正接との関係を，図によって求めること。

ｃ．加法定理の意味を明らかにし，これを用いていろいろな公式を導いたり，特殊な角の三角函数の値を正確に求めたりする。

２．三角形を解くこと。
ａ．精密な測量の必要なわけや，中学校で学んだ三角函数による直角三角形の解法を復習すること。

ｂ．角の小さい単位としての分・秒を知ること。および三角函数表について，その小部分が一次式で近似できることを理解して，比例部分を用いること。

ｃ．一般の三角形について余弦法則を見いだし，これを実際的な問題に用いること。

ｄ．一般の三角形について正弦法則を見いだし，これを実際的な問題に用いること。

ｅ．一般の三角形について正接法則を見いだし，これを実際的な問題に用いること。

３．微小な角に対する三角函数
ａ．角の単位としての弧度を知る。

ｂ．角の小さいところにおける正接・正弦の値を求めること。(その角を弧度で測った値にほぼ等しいことを認めること。)およびこれを用いて，天文等に出てくる微小な角を含む測量の問題を解決すること。

Ｃ．用語
基線，三角測量，加法定理，分，秒，弧度，ラジアン，正弦法則，余弦法則，正接法則，ヘロンの公式

§５．幾何の一般目標と指導内容

１．図形の基本的な性質を知り，それが実際的な問題の解決にあたって果している役割を理解する。

２．図形の性質を用いて，問題を解決する能力を養う。

３．目的に応じて，物の形を図形に書き表わす能力と，図形をうまく用いる態度とを養う。

４．図形に関する用語や記号を理解する。

５．証明の本質と必要とを理解し，論理的な考え方を日常生活にも用いるようにして，筋道を立てて論理的に考えていく習慣を養う。

６．日常生活においても，物事の筋道や数量についての関係を示すのに，簡潔な表現を用いる態度を養う。

７．図形によっては，それがものの動いた跡とみられることを理解し，ある条件に適する点の集合を，図形や式によってとらえる能力を養う。

８．簡単な図形について，これを式に表わしたり，その性質を式によって調べたりする能力を養う。

９．式や図形の特質の生かして，これをうまく用いる態度を養う。

1O．数学が文明の進歩の上に果している役割を理解し，数学に対する関心の深める。

１．次にあげたのは，幾何のおもな指導内容を，その配列の一例を用いて示したものである。この配列は，指導内容の配列の一つであって，ほかの見地から内容を別に組織したり，生徒の能力や必要に応じて，ある内容を省くとか，つけ加えるとかなどして，指導してよいことはいうまでもない。

２．この配列は，証明の本質とその使い方に対する理解を深めるとともに，しだいに図形の基本的でかつ有用な性質の理解を発展させていって，幾何の目標を達成しようとする考え方でつくられたものである。すなわち，次のような流れになっている。

　中学校の復習に次いで，幾何で用いられる方法をしだいに導入していき，これを空間にも適用して，基本的な公理をまとめる。この公理は，生徒がやさしく理解できるように広くとることにした。次に，これらに基いて，図形の性質をできるかぎり動的に，また解析的にとらえつつ，内容を展開する。(生徒にとって，理解することが困難で，しかも日常生活においても，数学一般においても，有用でないようないろいろな定理は省くことにした。)このようにして，軌跡の考えや代数的な方法についての素地をつちかっておいて，次には，幾何における解析的な方法を導入し展開しながら，一方では，幾何における対象を，円と直線から，いろいろな他の曲線にまで広げていった。

３．指導されるときには，生徒，学校の設備，教員組織などを考慮して，適切な方法を用いていただきたい。すでに「中学校・高等学校における一般学習指導法」が刊行されている。また「数学科の学習指導法」が現在執筆されている。これらの書物を参考にして，その一般的な方法を実際にうまく適用して，いっそう指導の効果をあげるように，指導の方法をくふうしてもらいたい。

Ⅰ．中学校の復習

Ａ．目標
１．幾何学的な事実についての用語の有用なことを知る。

２．三角形の合同・相似の条件についての理解を深める。

３．平行線の基本的な性質についての理解を深める。

４．中学佼で学んだ基本的な方法を用いる能力を伸ばす。

Ｂ．内容
１．中学校で学んだ基本的な幾何学的事実。
ａ．測量や縮図などで，どんな原理が用いられているかということや，三角形の合同・相似の条件を考えることの有用性を復習して，三つの条件をまとめること。

ｂ．工作や地図を用いるときなどに，平行線がどのように用いられているかを復習して，平行線の概念や，二つの平行線がどこでも距離が等しく，また方向も等しいという性質をまとめること。

２．中学校で学んだ代数的な技能
　ａ．長方形・三角形・平行四辺形などの面積や，直方体・立方体などの体積の公式をつくっていくときの考え方や，そのときに文字を用いることの有用なことを復習すること。

ｂ．ａ(ｂ＋ｃ)，(ａ＋ｂ)²，(ａ＋ｂ)(ａ−ｂ)などの展開式のように，よく用いられる基本的な恒等式について，図を用いたりなどして復習すること，およびこれを用いること。

ｃ．ａにあげた公式などについて，方程式を用いることを復習し，方程式を変形していく基本的な原理をまとめること。

Ｃ．用語
同位角，錯角，‖，⊥，≡，∽，∠，△

Ⅱ．幾何に用いられる方法を理解すること

Ａ．目標
１．帰納的な方法と演繹的な方法とを理解し，そのおのおのの有用なことを知る。

２．演繹的な推論における公理や定義の意味と，その必要とを理解する。

３．事実を条件と結論とに分析して，はっきりした形にいい表わしたり，その表現を確かめたりする能力を養う。

４．軌跡の考えの素地をつくり，必要に応じて，これを用いる能力をうる。

５．三角形が，直線図形の一つの基本的な要素と考えられることを理解する。

Ｂ．内容
１．図形についての性質の明確な表わし方
ａ．中学校における幾何学的な事項についての研究や，科学や日常生活における研究について，経験や実験から法則を帰納する過程を示すこと。

ｂ．中学校における幾何学的な事項についての研究や，科学や日常生活における研究について，正しいと認められた基本的な事実をもとにして，ある結論を導く演繹的な過程の例を示すこと。

ｃ．帰納的な方法と，演繹的な方法とを比較して，この二つの方法の特徴を明らかにすること。

ｄ．日常生活における討論などにおいて，明確な定義や，前提をはっきり述べることの必要なことの例を示すこと。

ｅ．これまでに学習した幾何学的事項について，用語を明確に定義したり，これからの研究において前提とすべき事項を選んだりして，まとめをすること。

ｆ．上の事実を，条件と結論とに分析して，はっきりした形に表わすこと。

２．幾何で用いられる方法
ａ．平行四辺形・長方形・正方形などの簡単な性質を研究するのに，演繹的な考え方がいかように用いられるかを明らかにすること。

ｂ．平行線・角の二等分線・線分の垂直二等分線などの基本的な図形の作図法を復習し，作図によって得られた図形を確かめるのに，演繹的な方法が有用であることを明らかにし，作図に関する問題を解くこと。

ｃ．平行線・角の二等分線・線分の垂直二等分線などの基本的な図形を，ある条件を満足する点が動いてできた図形として特徴づけ，これを具体的な問題に応用すること。

ｄ．実際の三角形について計算してみたり，いろいろな方法でためしてみたりして，三角形の内角の和が180゜であることを見いだし，これを演繹的な方法で確かめること。

ｅ．多角形を三角形に分解したり，またはほかの方法を用いたりして，上の定理を多角形の場合に拡張すること。

Ｃ．用語
公理，定義，証明，定理，条件，結論，作図，対頂角，内角，外角，余角，補角，線分，垂直二等分線，

Ⅲ．空間における図形の関係を理解し，用いること

Ａ．目標
１．平面からの類推などによって，図形の空間における関係を見いだす能力をうる。

２．空間における図形の基本的な位置関係を理解する。

３．帰納的な方法や演繹的な方法を用いる能力を伸ばす。

４．必要条件・十分条件の意味や，命題の逆の関係を理解する。

５．投影図を用いる能力を伸ばし，そのよさを知る。

Ｂ．内容
１．空間における点・直線・平面の概念と，その相互関係
ａ．工作や機械製作などの実際の場面で，平面をつくりだすのに用いられている方法を研究すること。

ｂ．上の方法のもとになっている事がらを，点・直線の相互関係によってまとめて考え，これを身のまわりにある具体物で示すこと。

ｃ．上でまとめた基本的な事実を，公理としてまとめること。

ｄ．教室・机・模型などの具体物の中に見られる，一つの平面に平行な平面や直線，または一つの直線や，平面にそれぞれ垂直な平面または直線を見いだすこと。

ｅ．平面上における平行や垂直の関係をもとにして，空間における平行や垂直の関係を数量的に明確に定義すること。

ｆ．同じ直線または平面に，平行または垂直な二つの平面，二つの直線，平面と直線の相互関係を明らかにして，平面上の場合と比較しつつ，これらの基本的な性質をまとめること。

ｇ．これまでに学習した基本的事実を公理としてまとめること。

ｈ．三垂線の関係を見いだし，証明すること。

注　ａからｇまでの事がらについては，生徒が実際の経験から考えたり，模型をつくったり，具体物を観察したりして，これらのことを見いだし，また，その例を示したり，ときには，反例をあげたり，模型をつくったりして，確かめていくことでじゅうぶんであって，生徒が少ない公理からこれを完全に証明していくことを考えているのではない。この１は，空間についての公理をつくるのがねらいである。

２．投影図
ａ．中学校で学習した投影図による立体の表わし方の基本的な規約と，その実際生活における有用性とを復習すること。

ｂ．各投影面上の三つの点が，空間におけるひとつの点を表わすための三つの点の相互関係についての条件を見いだすこと。

ｃ．投影面に対していろいろな位置にある直線や線分の投影図をかくこと。およびその各位置の特徴を明らかにすること。

ｄ．投影図で表わされた線分の実長を求めること

３．簡単な立体の性質
ａ．平面における三角形・長方形・正方形などから類推して，空間におけるこれらに対応するような立体を見いだし，定義すること。

ｂ．平面における正方形・長方形・平行四辺形などの平面図形の性質から類推して，立方体・直方体・平行六面体などの立体の簡単な性質を見いだすこと。

４．証明の本質
ａ．幾何における公理や定理の役割をまとめること。

ｂ．もしも，ある前提を認めるならば，それから演繹的に導かれる結論を認めなければならないことや，同じ前提に基いて，それから導かれた結論が異なるときは，両者の間に明示されない前提があって，これが異なっているのか，あるいは推論の過程に誤りがあるのかどちらかであることを明らかにすること。

ｃ．幾何や日常生活において，演繹的な推論が有用であることを明らかにすること。

ｄ．幾何や日常生活における必要条件と十分条件との例をあげ，これを比較することおよびその意味や命題の逆関係をまとめること。

Ｃ．用語
ねじれの位置にある直線，平面，空間，四面体，平行六面体，正多面体，必要条件，十分条件，帰謬法

Ⅳ．直線図形の性質を用いること

Ａ．目標
１．三角形の基本的な性質を理解する。

２．三角形の性質を，一般の直線図形に応用する能力を伸ばす。

３．代数的な方法を用いて，幾何学的な法則を実際問題に応用する能力をうる。

４．三角函数の理解を深め，その有用なことを知る。

Ｂ．内容
１．平行線に関係した三角形の性質
ａ．一つの三角形の一辺に平行な直線が，他の二辺をきったときにできる線分の間の比例関係を見いだし，証明すること。

ｂ．比例式を解いたり変形したりすること。これをａに適用して，二・三の定理を導くこと。およびこれらを実際問題に応用すること。

ｃ．上の定理を空間の定理に拡張すること。およびこれを応用すること。

ｄ．一般の図形についての相似の概念を明らかにし，相似の位置の考えを発展させること。およびこれを地図や写真の拡大などの実際問題に応用すること。

２．直角三角形の性質
ａ．測量などにおける三角比の使い方やその有用性を復習し，これを鈍角の三角函数にまで拡張すること。

ｂ．二角と一辺が与えられたときの三角形を解くこと。および正弦法則を証明し，これを応用すること。

ｃ．三平方の定理の証明をくふうすること。およびこれに関係した直角三角形の他の性質を明らかにし，これを具体的な問題に応用すること。(必ずしも平面に限らない。)

ｄ．二辺とそのなす角とが与えられたときの三角形を解くこと。および余弦法則を証明し，これを応用すること。

Ｃ．用語
比例式，中点，中線，重心，多角形，正弦法則，余弦法則，正弦，余弦，正接，余接

Ⅴ．円と球の性質を用いること

Ａ．目標
１．円や球の基本的な性質を理解する。

２．代数的な方法を用いたりして，円や球の性質を具体的な問題に応用する能力を伸ばす。

３．証明に演繹的な方法を用いる能力を伸ばす。

４．極限の概念を理解し，必要な場合にこれを用いていく能力をうる。

５．円や球の有用なことやその美しさを知る。

Ｂ．内容
１．円・球の対称性
ａ．円がその任意の直径に関して対称であることや，その中心のまわりに一回転しても変らないことを明らかにし，まとめることおよび円の弦・弧・直径の間の関係を見いだし，これを実際問題に応用すること。

ｂ．上のような性質を球の場合に拡張し，具体物について，その関係を示すこと。

ｃ．具体的な場面において，円の接線や球の接平面を見いだすこと。および円の接線・球の接平面を定義し，接線または接平面と接点をとおる半径との関係を明らかにすること。

ｄ．一直線と円，または二円の位置関係や，球についての同様な位置関係を分類し，それらの二つが接するための条件を求めること。

ｅ．円の中心角と弧との比例関係を復習し，用いること。

ｆ．道路・鉄道・機械などに円の弧が用いられていることや，その半径が曲り方の程度を表わしていることを明らかにし，具体的な問題についてこれを応用して，いろいろな長さを計算すること。

ｇ．三角形に関係した円を描くこと。

２．円や球の他の基本的な性質
ａ．円周上の一点から，その円の与えられた弧をみこむ角の大きさは，その点がその弧の共軛弧上を動いても変らないことを証明し，これを応用すること。

ｂ．接線を割線の極限の位置と考えて，上の定理から接線の性質を導くこと。

ｃ．円周上にない一定点をとおる直線と円によってできる二つの線分の積は，その直線がその定点のまわりを動いても，一定であることを証明すること。

ｄ．上の定理を球の場合に拡張すること。

ｅ．これらの定理を応用して，円や球の弦・半径・接線などの長さに関する実際問題を解くこと。

３．極限の概念
ａ．面積や体積の大きさの意味を復習し，極限の考えがそこに用いられていることを明らかにすること。

ｂ．内接正多角形や外接正多角形の極限として円周を考えて，円周や円の面積についての公式を導くこと。

ｃ．区分求積の考えを用いて，球・円すい・角すいなどの体積の公式を導くこと。

Ｃ．用語
接線，接点，割線，接平面，弧，弦，共軛弧，円周角，外心，内心，傍心，外接円，内接円，傍接円，共通接線，中心線，大円，小円，曲率，極限，区分求積，同心円

Ⅵ．軌跡の概念を発展させること

Ａ．目標
１．ある種の図形は，点の軌跡とみなすことができることを理解する。

２．図形に関して，座標の考えと代数的な方法を用いることによって，順序よく考えていくことができることを理解する。

３．図形に関して，代数的な方法を用いる能力を伸ばす。

４．規則正しい運動によってつくられる曲線の美しさを味わい，座標や軌跡の有用なことを知る。

Ｂ．内容
１．軌跡の概念
ａ．これまでに学習した軌跡の概念の背景となる事実をまとめ，ある種の運動によってつくられる図形として軌跡を定義し，この考えで，これまでの定理を見直してまとめること。

ｂ．上の基本的な軌跡に容易に帰着させることができる軌跡の問題を解くこと。

ｃ．ある与えられた条件を満足する点の運動によってつくられる美しい曲線を描き，その名まえを知ること。

２．座標と方程式
ａ．中学校で学んだ式のグラフの考えを復習し，軌跡の考えでこれを解釈すること。

ｂ．直線の方程式の一般形を用いること。

ｃ．一定点をとおるとか，ある直線に平行であるとかなど，特殊な位置にある直線の方程式についての条件を用いること。

ｄ．二点間の距離を座標で表わして計算すること。および円の方程式をつくること。

ｅ．方程式を用いたり，幾何学的な方法を用いたりして，円や直線に帰着できる軌跡の問題を解くこと。

３．二次曲線の方程式とその性質
ａ．放物線の定義から，その方程式を導くこと。およびこれを用いること。

ｂ．平行移動を座標によって表わすこと。および二次式のグラフや一般の位置にある円などについて，それを用いて研究すること。

ｃ．座標軸の位置を適切に選んで問題を解くこと。

ｄ．楕円や双曲線の標準形の方程式を知ること。

ｅ．二次曲線の簡単な性質を見いだし，これを証明すること。

Ｃ．用語
軌跡，サイクロイド，楕円，双曲線，放物線，焦点，準線，軸，二元方程式，平行移動，標準形，二次曲線