はしがき 中学校で指導するのに適当であると考えられる数学的内容は,前章において,生徒の生活経験との関係において,一覧表の形で示した。しかし,この示し方では,生活面との関係はめいりょうになるが,その反面,生徒の心の中に流れていく数学的な内容についての理解の発達のしかたは,明確に示されないうらみがある。
一方,第Ⅰ章においては,数学科の指導は,「理解」と「よさを知ること」とをもとにして,展開されなければならないことを述べた。
そこで,この章では,いろいろな数学的内容について,どのような理解がたいせつであるか,それがどのように発達していくことが,生徒にとって,円滑で,しかも効果的であると考えられるかを説明して,ひとつの系統的な発展の形を示し,指導の参考に供したいと思う。
もとより,理解の発達のしかたは,個々の子供によっても違うであろうし,また,その系統の立て方も,数学に対する見解によって,いくつかの違った系統をつくりうるものであるから,ここに述べる系統は,ひとつの参考例にすぎないことは当然である。
ここでは,次々の発展が,できるだけ,それまでに理解したことを逆転させずに,それを包括しつつ,しかも新しい内容を含んでいく,雪だるまのような発展のしかたを考えた。これは,試行錯誤をくり返したり,または,一つ一つばらばらに内容を理解していったりすることに比べて,能率的であり,また,理解したことの中核,すなわち,雪だるまの中核に当るものが,生徒に,より先のほうに発展していく見通しを与えるようになるという考えから,とったものである。
数学的内容の面からいえば,このような発展は,一つの樹木の成長にたとえることができよう。すなわち,生活経験という肥料によって,理解という幹や枝を,しだいに伸ばし,そのよさを知るという根を張って, しっかりした樹木となり,技能の花を咲かせるといえよう。
この際に,ここでとった系統は,むだな枝ぶりのない,まっすぐですっきりとした樹木の形を予想したといえる。
さて,以上のような考えで発展的系統を立てようとするとき,数学的内容は,その概念的な区別によって,いくつかに分類して考えたほうがわかりよい。われわれは,これを,次のように分けて考えた。
Ⅱ.分数
Ⅲ.正の数・負の数
§3 計量
§4 比および数量関係
Ⅱ.数量関係
§6 代数的表現
§7 図的表現
§8 簡単な図形
§9 実 務
この説明のしかたは,指導の実際に当って,この領域内における発達の中の二・三の段階を毎時間に指導し,その指導を通して,いつも,初め長所としてあげたようなことを感得させつつ,その時々の理解を,しだいに,初めに分析したものに発達させていくようにするということを,予想している。
§1.数
Ⅰ.十進数
A.十進数の長所
数を十進歩で表わすと,数の大きさを示すにもわかりよいし,数を用いた四則の計算も,簡単な原則をもとにして,きわめて機械的に処理できるようになる。
B.十進数についての理解
| 1.十進数の規約 |
各位の数字は,小数点の位置を中心として,左の方へ順次に1,10,100……と,それぞれ,前の位の単位を10倍にしたものを単位とした個数を示し,右の方へ順次に1/10,1/100,1/1000……と,それぞれ,前の位の単位の1/10を単位とした個数を示している。
| 2.小数点の位置 |
小数点の位置を,ある位のところに移すと,その位の単位を1としても,この数を表わした数が得られる。いいかえると,小数点の位置を動かすだけで,もとの数を10倍100倍,……,または1/10,1/100……にすることができる。
C.十進数についての指導
Bの1.十進数の規約は,すでに小学校で習得されたものとしてよい。中学一年で,小学校の復習として,整数・小数についての大小の比較や,整数の四則の筆算形式を復習している間に,Bの1の理解から,しだいに2の理解へ高めていくようにすることが必要である。
| 1.復習の留意点 |
(b) 2位数以上の数を乗数とする乗法の筆算形式における部分積をかく位置,乗数が10,100,1000,……の倍数である時の積の簡便計算法,除法の筆算形式における商の位取りの決め方,除数が10,100,1000,……の倍数である時の除法の簡便計算法などの復習において,Bの1の理解から2のような理解に高めていくことができる。このとき,特に,整数の末位に0をかき加えたり,末位の0を消したりすることが,10倍,100倍,1000倍,……したり,1/10,1/100,1/1000,……にしたりすることになることを明らかにしておくと,あとあとの指導が楽になる。
| 2.数範囲の拡張 |
上のような復習と平行して,または,それに続いて,数範囲を拡張して,億・兆の単位名や,十進命数法の規約を知らせつつ,この記数法によれば,10種の数字を用いるだけで,どんな大きな数も,どんな小さな数も表わされること。(特に,空位に示す0のはたらきを強調して)それらの取扱の原則は,これまでの原則(十進数の規約)がそのまま保たれていることを明らかにするがよい。この際に,ローマ記数法やその他の記数法との比較は,生徒の理解を助けていくことになるだろう。
| 3.三けたくぎり |
けた数の大きい数を取り扱うときに,三けた区切りが,世界でも,また日本でも,広く用いられていること。三けた区切りの数を読むときには,コンマのところの位が右の方から順次,千・百万・十億・兆……となっていることを知っていると便利であること。これらのことがらを理解させ,このような読み方になれるに従って,百万なり,十億なりを単位にして表わす方法,たとえば,120百万円のような,数の表わし方もあることを知らせていくがよい。(このときに,この読み方を,「ひゃく2じゅうひゃくまんえん」という読み方をせずに,「1おく2せんまん円」,または「百万円を単位として120」という読み方をするように指導した方がよい。)
| 4.小数の乗除に関連しての指導 |
中学一年では,十進数についての新しい計算として,小数による乗法・除法がはいってくる。この計算の方法をくふうするときには,さきに明らかにしたBの2の理解を基底において,これに結び付けて考えていくように指導するとよい。そして,小数を含んだ十進数の乗法・除法では,小数点の位置を除外すれば,いつも整数の場合の計算と同じであること。いいかえると,数字の並び方は小数点の位置に関係のないことを理解させ,小数点の位置の決め方のみを,新しく拡張された乗法・除法の意味から考えればよいことを明らかにする。そして,十進数を用いることによって,計算のために考えるべき点として,小数点の決め方と数字の並び方との二つに分解し,しかもそのおのおのが,きわめて機械的なルールによって処理できるようにすることによって,計算に伴う労力を軽減している点を感銘させていくがよい。
| 5.近似値の取扱における十進数 |
こうした計算法について,十進数のよさと意味を理解させていくことから進んだ機会としては,近似値を取り扱う場合がある。近似値の取扱を明らかにしていくのは,二年の仕事であるが,その背景としての概数や四捨五入・切り捨て・切り上げによる端数の処理のしかたは,小学校から指導されてきている。
| 6.四捨五入
正しさ・くわしさ |
四捨五入・切り捨て・切り上げという簡単な手順で,機械的に,よい近似値が得られることも十進数の利点の一つである。すなわち,ある位までの数字を保留して,その位より小さい部分を切り捨て・切り上げ,あるいは四捨五入するという簡単な操作だけで,その位の単位の1より小さい誤差で近似値が得られる。これは,分数などを用いた時には得られない利点である。
(たとえば,12/33の分母,分子の1の位を省略して10/30,すなわち1/3として,近似値が得られるが,このときの誤差については,一般的なルールがない。)
こうしたことを一年のころから理解させ,二年に進むにつれて,これに,くわしさ・正しさの概念を与え,十進数では,数のくわしさが有効数字のけた数で示され,正しさが有効数字の末位の1または1/2で見積られることを理解させて,これを四則計算に活用できるようにすることが,二年のおもな仕事である。
| 7.a×10nの記法 |
その際に,十進数の相対的な大きさを利用して,数をa×10nの形にかき直すことができること。こうすると,有効数字の0と,位取りを示すだけの0とを分離して示せることと,乗除の結果の見積りが10nの部分から容易にできることを明らかにし,このために,近似値の取扱がいっそう能率よくなることを感銘させることがたいせつである。
| 8.2,5などの倍数 |
なお,十進数のいま一つの利点として,2,5,4などによる乗除の簡便法があること,その倍数が容易に見分けられることなどがある。これらは,いつと限らず,適当な機会に指導していく程度でよい。
D.指導上の諸注意
十進法と時間のような六十進法との区別も,その機会を見て,はっきり指導することが必要である。
生徒によっては,10時25分を10.25時とかいて,十進法と同じように扱う誤りをよく見うける。
これは,小数点の意味を機械的にのみこんだことから起るものである。また,10時25分を10.時25とかくような習慣が一部に行われているが,これは,上のような子供の誤りを防ぐためからも,10:25のようにかいて,小数点と区別するようにしたほうがよい。
Ⅱ.分 数
A.分数の長所
分数は,除法の結果としての数値を,その除数および被除数といっしょに正確に表わしているので,理論的な取扱につごうがよい。しかし,大ききを人に伝える点では,明確を欠く。
B.分数の理解
| 1.分数の意味 |
分数は,分母にある数で分子にある数を割ったときの商を表わす。
| 2.分数の大きさ |
分数は,分母にある数を分母とし,分子が1である単位分数がいくつあるかを,その分子にある数で表わしているとみられる。
| 3.分数の相等 |
分数の分子・分母に同じ数をかけても,また,分子・分母を同じ数で割っても,その値(表わす大きさ)は変らない。
C.分数の指導
| 1.小学校との関連 |
| 2.中学校での重点 |
中学校では,これらの日常的な場合における分数の用法を主とするが,それにとどまらず,分数を一般的な数として自由に扱えるところまで高めることも必要である。たとえば,自動車の時速を毎時xキロメートルと表わして,この分速が必要なとき,これを毎分x/60キロメートルとし,これを用いて,その他の量を表わしたりする。これは,分数を,日常的な意味でのわかりよい表現というよりも,分数が一般的な数として,演算といっしょに,その結果である数を正確に示している利点を用いているのである。
このような用い方ができるためには,分数を除法の結果的な表わし方としてだけでなく,さらに,これに,演算を施していくことのできる数として理解されていなくてはならない。すなわち,分数は,量や比の大きさを表わす表わし方という程度の理解から,進んで,演算としての除法と同時に,その商を数として正確に表現して,量関係を正確に記述していくための理論的な数にまで高められなければならない。これが中学校での新しい仕事である。
このような理解をもってはじめて,数計算の場合に,分数を用いて能率のよい方法を考えたり,(125×25を,12500×1/4とするなど)計算の途中は分数を用いながら,必要な結果としての答には小数を用いて,分数と小数とを使い分けたり,分数の表現を用いて公式をかき,その公式をじょうずに利用したりすることができるようになる。(たとえば,S=a×b÷2というように,三角形の面積の公式をかいたとすると,これは,Sの求め方・計算のしかただけを示すにとどまる。これをS=ab/2とすると,計算のしかたを示すとともに,ひとつの数として量の大きさを表わす。したがって,たとえば,三角柱の体積Vを求める公式をつくるときに,V=ab/2×c=abc/2といったように簡単に計算することができる)
それゆえ,中学校での指導は,量を表わす分数から,計算の対象としての分数,一般的な関係記述の方法としての分数記法へと,流れていかなくてはならない。
| 3.量や比を表わす分数 |
量や比を分数で表わして,これを人に伝えたり,比較したりすることは,小学校での学習の復習として,まずなされることである。この際に,理解にあげた1.2.3.のおのおのを明確にしておくことが,後の発展のために必要である。そして,この機会に,小数による表わし方と比較して,分数による表わし方が,どんな場合に便利であり,どんな場合に悪いかを明らかにしておくがよい。
こうした理解が成り立つときは,量や比の大きさを概括して見通しをつけるような場合に,たとえば,99/215などを1/2とみなすように,数値をまるめて,簡単な分数として用いることができるようになるだろう。こうした用い方は,割合についての概算を手がるにしていくためには,便利である。(なお,比としての分数については,比の節参照)
| 4.分数の大小及び加減 |
分数の四則が,いつでも一定の方式でできることを理解するのは,一年の仕事である。その第一歩は,小学校の復習と,その発展としての大小の比較および加減であろう。
そのときの基本的な原則として理解さるべきことは,次の事がらである。
(b) 分数の単位をそろえるには,理解の3がもとになること。
(c) 単位分数と1との関係は,単位分数にその分母の数をかけたものが1になること。
(d) 以上のことをもとにすれば,分数の大小・加減は,整数の場合と同じであること。
(e) 分数は,最終の形としては帯分数で,しかも,既約な形にしておくことが,大きさを示す方法として,最も簡単な形であること。
| 5.分数の乗除 |
分数の乗除における生徒の理解の根本になることは,次の二つのことである。その一つは,分数をかけたり,分数で割ったりすることの意味(……の2/3を求めるときに,なぜ,……×2/3とかくかということ)で,いま一つは,乗除の計算の方法をどのようにするかということである。
このうち,乗除の意味については,整数についての乗除の意味からしだいに発展していくものであるから,これは次の節の四則において述べる。ここでは,乗除の意味がわかってから,その計算法をどうするかという点について考えてみよう。
計算法の理解の根底になることは,やはり,前にあげた理解の2.3である。このことをもとにして考えたものを,結果的にまとめたものが,よく知られた計算法である。たとえば,2/3×4/5を考えるときに,2/3を,1/3が2個あるものと考えたのでは,2を5等分できないのでゆきづまる。それゆえ,2/3の分数の値を変えないで,単位分数の数,すなわち,分子が5等分できるように変形できないものかと考えると,それは,分子を5×2とすればよい。したがって,2/3×4/5=2×5/3×5×4/5と考えると,これは,1/3×5が2×5個あるものの4/5であるから,1/3×5が2×4あることになる。こうした計算の過程を省略して,結果だけについてみると,分子の積を分子とし,分母の積を分母とする分数が,もとの二つの分数の積になっているということができる。
また,2/3÷4/5を考えるときに,この二つの単位分数を同じ単位で表わせないものかと考えると,それには1/3×5を単位とすればよい。したがって,2/3÷4/5=2×5/3×5÷4×3/5×3となり,この結果をまとめれば,被除数に除数の逆数をかけたことになっていることがわかる。
| 6.計算の洗練化 |
上のような指導においては,結果として洗練された形式を理解することは,計算を能率よくしていく上に必要なことであるが,これと同じ程度に,この結果にいたる途中の考え方も重要なのである。このような途中の考え方を上すべりにすることは,生徒たちに誤算の癖をつけていくもとにもなるし,生徒たちの自主的な研究態度を伸ばしていくのを妨げることにもなる。
それゆえ,上のように,意味を考えて,途中の過程を一歩一歩たどって計算していくことがはっきり理解されてから,さて,このような同じ考えをいつもくり返していくのは能率の悪いことであるが,何とかもっと手軽に,正しい結果が求められないかということから,計算の法則をまとめていくように指導すべきである。
このような計算法に習熟したら,さらに,これをもっと能率よく処理していくことも考える必要がある。
たとえば,2/3×6/7を計算するのに,
![]() とすれば計算がしやすいこと,乗除の混合の場合には,全部を一度乗法に直してから計算するほうが,計算しやすいことなどを明らかにしていくことが,計算を手ぎわよくしていく上に必要なことである。
とすれば計算がしやすいこと,乗除の混合の場合には,全部を一度乗法に直してから計算するほうが,計算しやすいことなどを明らかにしていくことが,計算を手ぎわよくしていく上に必要なことである。
| 7.整数・小数との関係 |
乗除の計算の指導の間に,これと平行して理解を深めていくべきことは,整数・小数と分数との関係である。すなわち,小数が10の累乗と分母とする分数であること,整数は1を分母とする分数とみられること(特に,1がa/aとみられることやab/aがbであること)を明らかにして,整数や小数を含めても,上で考えた計算法がそのままに当てはまることを理解させることが,計算をじょうずにしていく上に必要である。
| 8.分数を用いることの指導 |
分数が数として計算できるものであることが理解されてから後の指導は,どんな場合に分数を用い,どんな場合に分数を用いないかの区別を,はっきりさせていくことである。この場合の根底になることは,分数の長所にあげたことであろう。
このような指導の第一段階は,問題解決のための数計算における区別で,計算の途中では,手数を少なくするために分数を用いていくが,結果として量や比の大きさを人に伝えるためには,分数よりわかりよい小数を用いることなどがこの例である。(このような指導は,特に,二年,三年になって,方程式を用いて問題を解くときに必要になる,方程式の解法の途中の除法で,割り切れないために近似的な小数を用いていくと,明確さを失ってくる。また,数計算に手数がかかる。したがって,方程式の根を求めるまでは,分数で計算したほうがよい。しかし,その根を問題の条件に当てはめて,実際の量として考えるときには,なるだけ小数に直したほうがよい。)
| 9.文字を用いた分数 |
次に,文字を用いて公式や方程式を作る場合がある。このようなときに,÷の記号を避けて,数として扱える分数の形を用いていくことが指導されなければならない。
こうしたことから,文字で表わされた分数についての簡単な計算を,中学三年あたりで指導されてよいであるう。この場合に生徒が理解すべきことは,文字でかかれた分数についても,普通の分数と同じ原理で計算できることである。こうして,数という表現の世界から,文字を用いた変数という表現の世界へと,生徒の理解を高めていくことが,中学校での仕事である。
| 10.約数・倍数 |
約数・倍数は,約分とか通分とかの計算の際に,このような計算を機械化するために考えられたものとして扱う程度でよい。その際の理解事項としては,次のことがある。
(b) 十進数では,2,3,4,5,6,8,25,10などの倍数が,数字の並び方から判断できる。
Ⅲ.正の数・負の数
A.正の数・負の数の長所
正の数・負の数を用いて量を表わすことにしておくと,表現の形式が単一化される。いいかえると,表現の形式が同じでも,その意味内容が豊富になる。しかも,その取扱(計算)がまた簡単になるので,形式的に考えを進めていける点で便利になる。
B.正の数・負の数の理解
| 1.負の数の意味 |
| 2.符号の役割 |
十,—の符号は,そのあとにある数の正負を表わすものともみられるし,また,計算の記号ともみられる。
+3は,ひとつの数とみてもよいし,数直線上で正の方向に3だけ動かすという演算とみてもよい。また,−3は,0よりも3だけ小さい数とみてもよいし,数直線上で負の方向に3だけ動かすという演算とみてもよい。
| 3.四則の理解 |
正の数・負の数についても,正の数のみの場合についての四則の意味をそのまま拡張して,四則の計算をすることができる。正の数の場合に成り立つ演算の基本法則は,そのまま,同じ形式で成立する。
C.正の数・負の数の指導
| 1.準 備 |
| 2.量を表わすものとしての正の数・負の数 |
収入・支出とか,ゲームの得点・失点とか,資産・借金とかいうような,反対の性質をもちながら同じ単位で表わされる量が,正の数・負の数で表わされることから,指導が始まるのが普通であるが,この場合に,次のような点を明らかにしておくことが必要である。
(b) 増加・減少というような変化もひとつの量とみられ,正の数・負の数で表わされる。
(c) 正の数・負の数を用いると,たとえば,直線上に原点をとって,その右とか左とかいって方向をつけることによって,無限に広がった範囲にあるものを表わすことができる。
| 3.正の数・負の数の大小 |
こうしたことから,正の数・負の数が一定の順序をもつこと,その順序が正の数の範囲では,これまでの大小と同じものであることを明らかにし,大小の考えが,そのまま正の数・負の数の範囲に不合理なく拡張されることを理解させ,同時に,正の数・負の数が,量を表わすだけでなく,ひとつの順序に並んだものの位置を表わすことを理解させていくがよい。
| 4.正の数・負の数の加減 |
正の数・負の数についての加法・減法は,計算として正面きってとりあげる前に,すでに,正の数・負の数を量を表わすものとして用いるときに,しらずしらずのうちにはいっているといってよい。
たとえば,5円の損失を5円と赤字でかかないで,−5円とかくときには,(0−5)円と,この量が計算されるものであることを認めているのである。また,5円の増加を+5円,5円の減少を−5円と表わすときには,たとえば,8円から増減の結果が,この表記をそのまま使って,(8+5)円,(8−5)円と計算される点の便宜を認めて,+・−の記号を用いているのである。
こうしたことを学習していく間に,たとえば,
(利益)=(売価)−(もとで)
という表現が,正の数・負の数を用いることによって,損失の場合にも適用されていくというように,負の数を用いることが,形式を保持しようというねらいをもっていることを明らかにしていくことが必要である。そして,正の数・負の数にまで数を拡張した場合の,加法や減法の意味(たとえば,a+bはaからbだけ増えた量,または,aだけ増え,さらにb増えたときの結果としての増え方を表わす)を理解させ,次に述べる計算法についての理解の発達をまって,−bが+bの加法に関する逆元であること,ある数をひくことは,その数の逆元を加えることとみられること,これによって,加法・減法がひとつのものに統一されることを理解させることが必要である。
また,こうしたことを理解することによって,文字を用いて式を作ることが簡単になることも理解させるがよい。
| 5.加・減の計算法 |
上のような考えで,加法や減法の意味やその必要が明らかになると,これについての計算を能率よくするために,一般的な問題として,正・負の符号のあらゆる組合せについて,加・減の計算の規則を発見することが問題となるであろう。この必要性を背景として,具体的な例をとりあげてこそ,これから,一般的な計算の法則が生れてくるのである。
こうして,加法の規則・減法の規則が理解されたら,ついで,上に述べたような加・減の関係を理解させ,これを用いて計算するとよい。
| 6.正の数・負の数の乗法・除法 |
正の数・負の数の乗法・除法で生徒が最も困難を感ずるのは,乗法の意味,特に,なぜそんなものを考える必要があるのかという点であろう。これまでの指導において,公式などの形をそのまま保つように演算を拡張しておくと,場合場合で違った式を用いることなく,問題の性質に応じて一度式を作っておけばよいという点で思考が楽になることや,正の数・負の数が数として自由に扱えるためには,その計算法がはっきりしていなければならないことなどが明らかになっていないと,これからあとの指導に無理が生じてくる。これまでの指導でこうした点が明らかになっていれば,正の数 負の数について乗除の計算を考える必要も,また,その計算の意味や方法は,これまでのどんなことをもとにして,これを拡張していけばよいかということも,楽に考えられるだろう。
こうして,乗法が,ある量Aと,他の量BのAに対する割合を知って,Bを求める計算であるというこれまでの理解が,(四則の項参照:たとえば,時間A,距離B,BのAに対する割合としての速さをとって考えてみよ。)割合やA・Bの量に符号を考えても,やはり成り立つことを理解させていくがよい。
そして,乗法の意味が明らかになれば,符号のついた数の除法は,これと同様に,また,乗法の逆算として,やはり,今までと同じことになっていることも,理解されるであろう。
このようにして,乗法の意味が理解され,次に述べる計算の規則が理解されたならば,逆数の考えを負の場合をも含むように拡張して,加・減を一つにまとめたように,乗・除もまた,一つにまとめられることを理解させる。こうして,式を扱う場合に,和と積とが,その基本的な構成要素と考えられることを理解しやすくしておくがよい。
| 7.乗・除の計算法 |
乗・除の計算規則の基本は,その符号の法則である。これは,乗法の意味や必要がわかれば,いろいろな種類の手がかりから帰納させていくことができる。さらに,こうした符号の法則は,単なる積の計算だけでなく,かっこをはずすような式の計算のときにも役だつことを理解させ,その応用を広くするようにしたほうがよい。
| 8.さらに進んだ指導 |
こうして,正の数・負の数が,計算のできる数として確立されたならば,そのあとは,この見方で,いろいろな数量的な処理の原則や方法を単純化・機械化していくことが必要になる。この機会としては,式の計算(同類項の簡約・かっこの用法),方程式の解法(移項の法則,一般の形にまとめること),公式の変形などがある。
これとともに,正の数・負の数の意味を考えたり,加法・減法を考えたりする時に用いた数直線を一般化して,数と直線との対応を明らかにしていくことが,座標の考えを理解していくために必要になる。
座標平面や,その上の直線の方程式が,自由に扱えるようになってはじめて,正の数・負の数の理解が確実になったといってよいであろう。
§2.四 則
A.四則計算の長所
四則の計算を用いることによって,既知の量や数,あるいは,より容易に測定できる量から,必要な量や数を,正確に,しかも能率よく求めることができる。
B.四則についての理解
| 1.四則の意味 |
(b) ある量と,それから変化したときの変化の大きさを知って,変化の結果を求めるとき
b.もとの量と,変化したあとの量を知って,変化の大きさを求めるとき
(4) 除法は,次のような場合に適用される。
(b) ひとつの量の大きさと,その量の基準に対する割合を知って,基準の量を同じ単位で表わすとき
| 2.四則の間の関係 |
(2) 乗法と除法とは互に逆の関係にあり,除数の逆数をとれば,除法は乗法になる。
(3) 乗数が整数の場合には,乗法は加法の特別な場合にみられる。
| 3.計算の方法 |
(2) 加法(および乗法)においては,数の順序を変えて加え(かけ)ても,和(積)は変らない。
(3) 加・減の計算は,そろばんを用いると能率的である。
(4) 乗・除の計算は,計算尺を用いると能率的である。
四則の計算については,既知の数・量と未知の数・量との関係がわかっているとき,その既知の数量から,未知の数量を求めるのに,すぐに,どんな計算を適用してよいかが判断できるようにすること,および,その判断が一度下されれば,あとは機械的な手続きの適用として,問題の関係から思考をきりはなし,簡単に,しかも正確に問題が解決されるようにすることがたいせつである。
それゆえ,ある量を求めることが必要になって,問題の場面を一度文章で表わしたならば,その文章の中にある数量とことばから,どんな計算が必要であるかが機械的に判断できるようになること,その数字に基く計算ができるだけ機械的になるようにすること,さらに進んでは,問題の場面から,このような解決を可能にするように,必要な数値と関係を取り出すことができるようになることがたいせつである。
| 1.復習の要点 |
さて,小学校においては,数の四則については,次のようなことを学習してきている。
(2) 乗数・除数が整数の場合の乗法・除法の意味
(3) 整数・小数・分数(同分母の場合)の加減の計算
(4) 乗数・除数が整数の場合の整数・小数・分数の乗除の計算,除法における被除数・除数・商・余りの間の関係
| 2.加・減の指導 |
加法・減法では,小学校で学習した加減の意味を明らかにし,日常に用いられる加減を指示することばについて理解を深めるとともに,諸等数や分数などを含めて,計算の基本原理として単位をそろえること,上位の単位と下位の単位との関係に基いて,繰上がり・繰下りが行われることの理解を深めていくのが,一年の仕事である。二年になって,正の数・負の数を扱うときになって,加・減の意味は,小学校で学んだものから,全体・部分という関係にこだわらない意味(すなわち,さきに四則の意味のところにあげた(1),(2)の(a)から(b)のほうに)にまで高めていく。同時に,文字式についての計算において,同類項の考えが,数の場合の単位に相当するものであり,同類とみられない項の間には,繰上がり・繰下りのないことを理解させることが必要である。
| 3.乗・除の意味 |
乗法については,小学校では,累加として理解してきているとみてよいであろう。また,除法については,包含除・等分除の意味を理解してきている。中学校では,これらの復習から指導が始まるが,乗法について,いつまでも累加の意味にだけとどまっていると,小数や分数による乗法や除法の意味が理解できず,これらの用法や比例の概念などの指導がむずかしいものになる。
累加としての乗法から,一般の乗法へと高めていくには,次のような段階を経ていくのが妥当であろう。
(2) 除法は,乗法の逆の計算であって,次の二つの場合があること。
(b) Bは,どんな数をA回加え合わせたものか。
(4) このように,BをAで割った数は,加え合わせる回数というよりも,Aを単位にしてBを測った値、すなわち,BのAに対する割合と考えたほうがよい。
(5) Aを基準にしてBを表わした割合が整数になるときは,Aと同じ単位でBを表わそうとするには,Aにその割合をかければよい。
(6) Aを基準にしてBを表わした割合がq/pになるとき,BをAと同じ単位で表わそうとするには,Aをp等分したものを基準に考え,その量をq倍すればよい。
(7) Aを基準にしてBを表わした割合が小数や分数になるときも,Aと同じ単位でBを表わすのに,Aにその割合をかけることにしておくと,割合が整数でも,小数・分数でも,同じ考えの場合が同じ計算で表わせるから便利である。
すなわち,除法の商の意味が,単なる累加の回数から,一方を基準にした他方の割合(あるいは,一方を単位にして他方を測定した価)にまで高められていること,除法と乗法とが互に逆の演算であることが,前もって理解されていてはじめて,比の計算としての乗法が理解されるのである。
こうして,乗法の意味が発展してくれば,除法の意味もそれに応じて,次のように発展する。
除法には,次の二つの意味がある。
(8) B,Aが同じ単位の量を表わすとき,B÷Aは,Aを単位にしてBの大きさを表わす。いいかえると,Aを基準にして,BのAに対する割合を求める計算である。(前の(2)aの発展)
(9) pが,Bをある量を基準にして表わした割合であるとき,B÷pは,基準の量を,Bと同じ単位で求める計算である。(前の(2)bの発展)
| 4.乗・除の意味の発展 |
こうして,乗・除の意味を理解していくとともに,実際の場合に,どんなことばを用いてこの関係を表わしているかを知り,この言葉の種類をしだいに豊かに知っていくように指導し,ある機会にこれをまとめてやることも必要である。
ついで,AのBに対する割合は,BのAに対する割合の逆数になっていることの理解から,除法は乗法の逆の計算であることの理解を深め,逆数の考えを用いれば,除法で表わした計算は,乗法で表わすことができることを理解させるがよい。このようにして理解を深めていくならば,たとえば,S=abやS=b/aのような関係式に基いて,Sとbとの比例の関係を認めていくことが容易になるであろう。
| 5.四則の計算法 |
整数の加法や乗法の復習の間に,交換・結合・分配の法則を明らかにし,われわれの用いている計算法が,これらの法則を利用して,数の計算をより簡単な場合の計算に帰著させて,計算法を機械化していることを理解させ,この理解に基いて,しだいに計算法をくふうし,必要に応じて,いろいろな簡便な計算もできるようにしていくことが必要である。このような例としては,25をかけるかわりに4で割る計算とか,そろばんの計算で,258を引くかわりに1000を引いておいて742を加えるとかいう例がある。
そろばんの使用については,小学校では,加・減について基本的な理解とある程度の技能が,身についているものとしてよい。中学校では,この技能を,さらに,正確さと速さとが増すように伸ばしていくことが必要である。
乗・除の計算については,乗数・除数が整数である場合について,小学校で指導してあるから,上にあげた法則の理解と,十進数・分数の意味,新に拡張した乗法・除法の理解とに基いて,乗数・除数が,小数や分数の場合にまで拡張し,その技能を身につけることが,中学一年での仕事である。(十進数及び分数の項参照)
| 6.計算尺による乗・除 |
乗・除の計算法としては中学二年になって,計算尺による方法が指導されることになっている。この場合に,次の二つのことをはっきり理解させる必要がある。その第一は,乗・除の場合の位取りの決め方であり,その第二は,乗・除の場合の目盛の読み方である。
第一の方は,積や商の第1位を概算して位取りを決める(たとえば,概算の結果が9×103となり,目盛の読みが1.05となれば,10500を答とする)ことを理解させていけばよい。
目盛の読み方としては,次の三つのことが理解されなければならない。
すなわち,読みの誤差を1目盛の1/2として,初めの例の計算尺では,相対誤差の限界は,次のようになる。
2〜5 〃 1/2×.05÷2=.012
5〜10 〃 1/2×.10÷5=.01
2〜5 〃 1/2×.02÷2=.005
4〜10 〃 1/2×.05÷4=.006
(3) 除法では,D尺に被除数をとり,その目盛にC尺の除数の目盛を合わせれば,C尺の1また10の下のD尺に,商を示す目盛が来ること。
次に,乗法・除法の目盛のとり方を理解させていくのであるが,このときも,初めは目盛線にきっちり合うような数値で,原理を理解させ,ついで,目盛の端下を読むような場合に移るがよい。そして,この間に,カーソルやC尺・CI尺の動かし方(両手の指をかけて,左右から力を働らかせつつ移動させ,移動が円滑にゆっくりといくようにする。)を指導するがよい。
こうして,くわしさに対する理解の発達をまって,計算尺は乗・除の計算に便利な道具であること,計算尺による計算では,数値のくわしさが自然にそろってくることなどを,理解させていくがよい。
§3.計 量
A.計量の長所
どんな量を表現しようとしているかを考えて,その目的に応じた単位とくわしさとで,量を数に表わしておくと,量の大きさが明確に示されるので,その量についての判断が客観的になる。
B.計量の理解
| 1.測定の意味 |
この基準にする量は,その大きさが客観的なものであって,他の基準の量との関係が,計算につごうよくできているものほど,目的にかなう。
| 2.測定の方法 |
計器をくふうして,計器の目盛を読んですぐわかるように(たとえば,電力のメーターのように)するか,もっと容易に測定できる量をもとにして,これから計算して求めるように(たとえば,長方形の面積の公式のように)するかなどして,できるだけ測定の労力が少なくてすむようにしている。
| 3.測定値 |
測定して得る値には,個数を直接数える場合を除いては,いつも誤差が伴っている。この誤差の大ききは,正確にはわからないが,その測定の方法から,どの程度以下であるかは判定できるし,また,必要に応じて,測定の方法をくふうすれば,もっと小さくすることもできる。
C.計量についての指導
計量についての指導は,大きく分けて,直接測定による場合と間接測定による場合とになる。直接測定は,主として中学一年で指導され,間接測定は,中学二年で指導されるとみてよい。
| 1.直接測定の指導 |
中学一年では,長さ・角・時間・時刻・ます目・重さなどの基本的な量について,小学校からの学習をまとめることから指導が始まる。そして,どんな場合にこれらの量を用いたらよいか,どんな計器で,どんな単位で,どのようにして測るかなどを理解させるのが,おもな仕事である。ここで,中心となる理解事項としては,次のようなことが考えられる。
(2) 各種の量の単位および単位系を知ること,特に,メートル法の組織と,これが世界的のものであり,十進法をもとにしている点で,他の制度よりすぐれていること。
(3) 単位を選ぶときには,次の点を考えること。
(b) 量の数値を他の量に関係して用いるときには,他の量はどんな単位で表わすかも考えて,単位および単位系を選ぶ。(たとえば,建物をつくるのに土地を測る場合,建物の規格が尺間で表わされているときは,尺間を用いる。)
(c) 位取りを示す0が,なるだけ少なくてすむように,単位の大きさを決める。
(b) 測ろうとするものの大きさを概測し,その大きさをできるだけ少ない回数で測りきる計器で,しかも必要な最小目盛のついているものを選ぶ。
そして,測定して得られる値には,避けられない誤差のあることに,漸次,目を向けていくがよい。こうした測定値をいかに処理するかは,間接測定のような,誤差の大きくなりやすい測定の発展をまって,中学二年で指導していくのが適当である。
| 2.各種の量の意味 |
なお,各種の量が,どんな場合に必要になるかのまとめの例を,次にあげてみよう。
(b) 面積・体積・速さなどの,他の量を計算するもとにする。
(c) 幅の一定な長方形状のもの(布や板),断面の一定な柱伏のもの(糸,柱,パイプ)などの量を表わす。
(b) 方位や位置を定める。
(b) 能率や速さなどの,他の量を計算する。
(c) 行動を記録したり計画したりする。
(b) 力の大きさを表わす。
(b) 粒状の物質の量のだいたいを知る。
| 3.ヤード・ポンド法および計量法についての指導 |
なお,単位系として,ヤード・ポンド法の単位系については,英米では,これが主として用いられていることを知らせ,そのメートル法との換算の方法を理解させればじゅうぶんであって,換算の率や各種単位間の関係を覚えさせることは必要ではない。また,度量衡原器や各種単位の発生の歴史などの話は,単位のもつ社会的な意味を理解させるのに役だつであうう。しかし,このような知識は,それ自身として,重要なものではない。
直接測定の指導で,知識として重要なことは,次のことである。
(2) 国家の検定した印のある計器によらなくては,取引や公の証明に必要な計量をしてはならない。
第六十八条(使用の制限)計量器でないもの,および,次の各号の一に該当する計量器は,取引上又は証明上における法定計量単位による計量に使用し,又は使用に供するために所持してはならない。
一、その者が修理した後,まだ,検定又は比較検査を受けない計量器
二、第六十六条第一項に規定する計量器(検定証印又は比較検査証印が附されていない計量器,検定に合格したもので,検定の有効期間を経過したもの,比較検査に合格したもので,比較検査の有効期間を経過したもの)
第七十二条(正確に計量する義務)政令で定める物象の状態の量について,法定計量単位により取引又は証明をする者は,政令で定める誤差をこえないように,その量を計らなければならない。
第七十八条(精度の制限)法定計量単位による質量による取引であって,その一回の取引量が10キログラム以下であるものについては,天びんを使用する場合を除き,その取引量の10分の1以下の最小目盛を有するはかりを使用しなければならない。
第七十九条(はかりの表示最大量)はかりを取引上又は証明上の計量に使用するには,その最大目盛の示す量をこえる量を1回に計ってはならない。
第八十条(水平装置)計量器の位置が水平であるかどうかを定めるための装置を有する計量器は,その位置を水平にした後でなければ,取引上または証明上の計量に使用してはならない。
第八十一条(零点の調整)零点を調整する装置があるはかり又は検位衡は,その零点を調整した後でなければ,取引上又は証明上の計量に使用してはならない。但し,天びんは,この限りでない。
第八十二条(ますの使用制限)木製ますは,第八十九条第一項第一号の政令で定める穀用ますでなければ,穀類(米,麦及び通商産業省令で定める雑穀をいう。以下同じ。)について,同号の政令で定める液用ますでなければ液体について,取引上又は証明上の計量に使用してはならない。
第八十三条(同上)取引上又は証明上において20立方デシメートル以上の穀類の量を計る場合において,20立方デシメートルの倍数である部分を計るには,全量20立方デシメートル未満のますを使用してはならない。
| 4.測定値の処理 |
測定値の性質については,一年のころからしだいに理解を深めていって,二年になって,その適切な取扱方を問題にしていくようになっている。この間に,次のようなことを,主として,理解させていくがよい。
(2) 近代の産業の発達は,よりくわしい測定の必要を生み,これに答えるために,いろいろな測定の方法が考案されていること。
(3) 測定値の正しさが特に必要となる場合には,数回くり返して測定し,その平均を求めることが必要であること。
(4) 測定値をもとにした計算では,いつも,その数のどの位の数字までが意味があるかを考えて,端下を処理することが必要であること。そのためには,乗除の計算では,くわしさをそろえ,加減の計算では,正しさをそろえていくことが,能率よい方法であること。
| 5.直接に測定できるようにするためのくふう |
二年,三年と進んで,比例に対する理解が深まってくるに応じて,その応用として,次のようなことを理解させることができる。すなわち,われわれは,できるだけ直接に測定することによって,手軽に量の大きさを知ろうとして,いろいろな器具をくふうしている。そして,その場合に,いろいろな比例関係をもとにして,目盛を等間隔にして,読みやすいようにくふうしている。このような例としては,温度計・さお秤・バネ秤・雨量計などがある。
| 6.間接測定の指導 |
間接に量を測ることについて,小学校から指導が続けられるのは,面積・体積である。これらの量がどんな必要から考えられたものか,何を単位に測るかということ,および辺の数値が整数の場合の長方形の面積,直方体の体積などについては,小学校で指導されているものとしてよい。
中学校では,これらの復習から指導が始まって,中学一年では,辺の数値が小数・分数の場合にも,長方形・直方体の求積公式がそのまま成り立つこと,および各種の日用単位の相互関係が指導される。中学二年になって,平行四辺形・三角形・台形・円の面積,および柱体・円すい・角すいなどの求積公式が指導される。
これらの公式の指導において,重要な理解事項は,次のことである。すなわち,
「規則正しい図形については,その面積や体積は,これを直接に測るよりも,もっと容易に測定しうる各部分の長さをもとにして,計算して求めることができる。こうしたくふうによって,直接に測る労力をずっと節約できる。」
求積公式そのものの理解については,しいて,全部を,演繹的に証明する必要はない。簡単に合同な図形を動かして証明できるものは,そのような方法によってもよいが,それ以外のものについては,実験的・帰納的に確めていく程度でよい。
また,求積公式のないものについても,いろいろなくふうによって,直接あるいは間接に面積・体積が求められることを理解させることも重要である。
このような場合の理解事項としては,多角形や正方形による曲線図形の近似,相似比と面積・体積の比との関係,密度一様な物体の目方と体積との関係などがある。
(2) 長さの間接測定
長さの間接測定としては,二年において,円周および直接測れない二点問の距離の測定が指導される。円周の測定については,円周と直径との比例関係をもとにして,より正確に測定しうる直径の測定に帰着させることを理解させる。また,直接には測れない二点間の距離については,三角形の決定条件をもとにして,直接測定しうる辺や角をもつ三角形の一辺としてその距離を考え,その三角形を決定していくことによって,測定しうるものに帰着させることのできることを理解させることが,おもな仕事である。
二年においては,距離の間接測定は,縮図をかくことによって解決される。三年では,この解決の方法をより正確なものとするため,図をかくことに伴う不正確さを避け,直接測定した数値だけに基いて,計算によって必要な量を測定しようという目的から,三角比や三平方の定理を用いた解決が指導される。この問題をとりあげるときには,長さの測定が,角の測定より手数がかかるが正確に行われること,角の測定をより正確にするために,トランシットのような器具がくふうされていることを,知らせていくがよい。
このような解決の根底になる理解事項としては,図形の節にあげた,三角形の決定条件・相似の概念・比例定数としての三角比の意味,および比例の概念などがある。これらについては,それぞれの項を参照されたい。
(3) その他の量の間接測定
このほかに,間接に計算を用いて測定される量として,速さや目方などがある。これらについては,直接測定される量と,これから求めようとする量との関係を理解させることが根底である。(たとえば,速さのときはv=8/t(vは速さ,sは距離,tは時間),vの単位はtの単位およびsの単位に対応する単位とすること。目方のときはw=kV(wは目方,Vは体積,kは密度),kの単位は,wおよびVの単位に対応する単位とすること。)
| 7.概 測 |
概測についての指導は,小学校から行われている。この概測についての重要なことは,次の事がらである。
(2) 概側が正確になるようにするには,標準となる身近なものの大きさに親しんで,これをものさしとするとよい。
こうした理解をもとにして,長さや方向・目方などについて,ある程度の測定の能力をもたせることは必要なことである。
| 8.その他の場合の測定 |
量を数で表わす場合として,以上のほかに,個数を数える場合と,平均値などによって集団の傾向を表わす場合とがある。これらについては,やはり,上に述べた基本的な理解事項の多くは,そのまま当てはまる。その指導において注意すべき点は,次の点である。
(2) 集団の傾向を代表するものとしては,その集団全体,または,その見本についての平均値を用いることが多い。この平均値も,誤差を含んだ数である。
(2) 穀量をます目で測ることは,一種の概測であり,だいたいの見当をつけるためのものである。したがって,正確を期す場合,たとえば,取引などにおいては,目方によるほうがよい。統計などで,ます目で数量を表わしているのは,古い統計との比較の便宜上,目方で測ったものを一定の換算率で換算したものである。
(3) ヤード・ポンド法については,各単位が,どんな量の単位であるかを知らせ,かつ,換算表などを利用して,メートル法との換算ができればじゅうぶんであって,これ以上のことは必要はない。
(4) これまで,10平方メートルということばとともに,10メートル平方ということばが用いられ,一辺10メートルの正方形を意味していたが,このようなまぎらわしいことばは,用いないほうがよい。
なお,生徒は1km2=1000m2のような誤りをしやすい。1km2などの記号が,何を意味するかという点の理解が,ふじゅうぶんであるからであろう。
(5) 生徒は,やたら小さい単位までの数字を求めることを,くわしい測定と考えがちである。有効な数字がどこまでであるか,どこまで必要かなどを考えて,目的に合った取扱をすることこそ,正しい測定であることを,じゅうぶんに理解させてほしい。
(6) 計器の目盛が2とびになっているようなとき,目盛り線の値を読んだり中間の値を読んだりするのに,1とびの場合とまちがいやすい。1目盛がいくつに当るかをいつも念頭において,目盛を読むような習慣が望ましい。
(7) 計器の取扱を乱暴にすると,計器の寿命をいためる。どのような取扱が,どのように寿命に影響するかを,よく理解させることが必要である。計器を取り扱うときは,いつも両手を用いて,一方で操作し一方でささえるような習慣が望ましい。
§4.比および数量関係
Ⅰ.比および比例
A.比および比例の長所
比は,二量の関係のしかたを数量的に表わす一つの方法で,これによって,一方の量や二量の関係のしかたをわかりやすく示したり,関係のしかたを比較したりすることが容易になる。
(2) 比例の長所
変化する二量の比が一定であることを見いだしたり,一定とみなしたりして,ものごとがうまく解決される場合が多い。すなわち,このときには,一方の量についての事実をもとにして,他の量についての必要な事実が,手軽にわかって便利になる。
| 1.同種の量の比の理解 |
同種の量についての比は,一方が他方の何倍になるかという関係を表わす。この場合には,両方を同一の単位で測りさえすれば,何倍かという数値は,単位によって変らない。(この数値を比の値という)
| 2.異種の量の比の理解 |
異種の量についての比は,一方の単位量当りの他方の量を表わす。この場合には,それぞれの単位を決め,その単位で表わした数値の比を用いる。この比の値は,用いた単位によって異なるから,その単位を明示しなければならない。(たとえば,人口の面積に対する比は,人口密度といわれている。これは,面積を表わす単位として,km2をとるか,平方里をとるかによって,値が異なる。)
| 3.比の値と二量の大きさの関係の理解 |
比の値と,基準になる量の大きさとがわかっているときは,その基準の大きさに比の値をかければ,比で表わされた量の大きさが,基準の量と同じ単位を用いて求められる。
| 4.比例の理解 |
二量ABが比例していて,Aがx1,x2,x3,……の値をとるとき,Bがy1,y2,y3,……の値をとるように対応していると,
(2) 一方がk倍になれば,他方もk倍になる。
すなわち,x2=kx1,ならばy2=ky1
(3) 和には和が対応し,差には差が対応している。
すなわち,x3=x1+x2ならばy3=y1+y2
x3=x1−x2ならばy3=y1−y2
| 5.その他の比例 |
C.比および比例の指導
小学校では,同種の量についての比の意味や比の値について,ごく簡単な場合について指導され,比・比の値・割合・百分率・パーセントなどのことばに親しんできているものとしてよい。
中学校では,これらのことの復習から始まって,比が広く社会で用いられていることを理解し,そのいろいろの用い方に親しんでいくとともに,進んで,これを適切な場合に自由に使えるようにしていくことがおもなねらいである。そして,中学校におけるおもな指導内容の多くは,この比の考えを用いるためのものであり,また,比の応用であり,発展であるといえる。(数計算・経済的な応用・指数・比例・相似・三角比など)
したがって,この比の考えをはっきり理解し,これをいろいろな場面に使いこなしていけるようにすることは,中学校数学科の指導のねらいの大部分を占めているといって,過言ではない。
| 1.小学校の復習の要点 |
中学校での発展は,だいたい,次のように考えられる。まず,小学校の復習として明らかにすべきことは,次のことである。
同種の量について比を用いる場合
(2) a:bの形に比を表わしたときには,a,bのどちらかを特に基準とするということなく,その関係を表わしたものである。この比の値を考えるときは,bのほうを基準とすることに規約している。
(3) 比の大小・相等は,比の値によって決める。
(4) 「……のわりに」というときの……は,比較の基準と考えられる。
この基準にする量Aの大きさが同じではないときは,それに対する量Bの大きさを,そのままで比べても,BのAに対する関係を比較したことにはならない。このようなとき,BのAに対する比の値を用いると,比較が明確にできる。
(5) わかりよい量を基準として,他の量をそれの何倍ということで表わすと,その量をわかりよく伝えることができる。(二つの量の差が問題であるとき,その差が小さいときは,片方を基準にして,他方のそれとの差で表わすことも,わかりよい方法であるが,その他の場合には,この目的に対しては,多くは比が用いられている。)
(6) 同種の量の比の値は,整数・小数・分数・百分率などで表わされる。
(7) 小数の大小はやさしく判定できるので,割合の大小を比べるには,小数を用いると都合がよい。
(8) 分数では,単位としてどんな単位分数でも用いることができるので,割合を,もとの数をそのまま用いて表わそうとするにはつごうがよい。
もとの数がきっちりした数のときには,分数は正確に割合を表わす。
(9) 百分率は,分母が100である特別な分数の分子に当る数を用いて,割合を表わしたものである。
| 2.中学一年の指導 |
こうした理解をもとにして,比の意味を,同種の量についての場合から,異種の量についてのものに広げて,比の用いられるいろいろの場合を通して,比の用い方の理解を深めていくのが,一年としてのおもな仕事である。そして,この間において,理解すべき事がらは,次のようである。
(b) 異種の量の比の値は,単位をもった数値である。((a)の例で,1個当り何円,1km2当り何人,また,速さのような場合は,キロメートル毎時など)
(c) 異種の量の比を比べることができるのは,比の値の単位が同じ種類の場合についてである。
(d) 異種の量の比についても,小学校で学んだことのうち,(1)から(4)までは,そのままなり立つ。
(b) 百分率は,基準を100として,比の値を表わしたものであり,これによって,小数を避けて,比の値が表現できること。
(c) 歩合は,小数で表わされた比の値の読み方であること。基準になるのは,10割であること。
(d) 比の値を求める計算は,わり算であること。
(e) 基準になる量に比の値をかけた積が,その量の大きさになっていること。
(f) Bを基準にしてAを表わした比の値は,Aを基準にしてBを表わした比の値の逆数になっていること。
(3) 比の計算の指導
(b) 比の値が分数のときは,単位分数に当る量は,基準量を単位分数の分母で等分して求められる。これを,新しい基準量とすると,これに対する求めようとする量の比は,その分子の数で表わされ,(a)の場合になる。
(c) 比の値が百分率で表わされているとき,基準量を100等分したものを新しい基準量とすると,もとの量の新基準量に対する比の値は,百分率の数値そのままになる。
(4) 比を用いる場合の理解
(b) (a)の比較は,AのBに対する比が,適当な条件のもとで一定とみられるとき,特に有効である。
(c) 溶液の濃さ,物の成分などのように,全体に対する部分の量の比が一定とみられる場合には,その見本や一部分についての比の値を調べておくと,全体の量がわかれば,いつでもその部分の量を,計算によって求めることができる。
(d) 上のような場合に,その比の値が,そのものの質を表わす尺度とみられる。
(e) 比の値は,このように,一方の値から他方の値を知るための手段としてではなく,二つの量の関係の尺度として用いられることがある。利息を表わす利率などは,この例である。
(f) いくつかの量の比によって,物を配分したり調合したりすることが多い。このようにすると,その量の重要性に応じた配分や調合ができる。
| 3.中学二年における比の指導 |
二年になって指導することは,根本において,上と同じことである。それに加える新しい内容をあげると,次のようである。
(2) 基準の量を表わす数値としては,1,100のほかに,1000,10000などが用いられることがある。これは,1や100を基準にしたとき,比の値があまり小さくなって,空位を示す0が多くなることを避ける場合に用いられる。
(3) 指数は百分率の特別な場合であって,基準時の量を100として,他の時期の量を表わしたものである。
(4) 指数の値は,その量を表わした単位のとり方に依存しない。
(5) 指数を用いることによって,単位の異なる量,しかも時間的に変化していく量の変化を,指数の数値の大小だけで比べることができる。
| 4.比例の指導(二年) |
こうして,比についての理解が深まっていくについて,二量が比例して変化する場合の多いことに気づくであろう。その関係のしかたを表わすことばとして,比例を導入してくることが,一つの仕事である。すなわち,
(2) 変量x,yの関係がy=ax(aは定数)で表わされるときは,yとxとの比が一定であること。すなわち,yはxに比例すること。
(3) yがxに比例するということと,xがyに比例するということは,同じことであること。
(4) yがxに比例るときは,xが2倍,3倍,4倍,……となれば,yもそれにつれて,2倍,3倍,4倍,……となること。また,xのほうの和には,yのほうの和が対応し,xのほうの差には,yのほうの差が対応していること。
(5) 比例の関係をグラフにかけば,原点を通る直線となること。
(6) この直線の傾きは,比例定数によって決まること。
(7) 変量x,yについて,xy=aの関係があるときは,yと1/xとの比が一定であること。すなわち,yは1/xに比例するとみられること。
(この場合に,yはxに反比例するという。)
(8) yがxに反比例するときは,xが2倍,3倍,4倍,……となれば,yは,それに応じて,1/2,1/3,1/4……となること。
(9) 反比例の関係をグラフにかくと,一種の曲線となり,その曲線の形は,定数項が違っても同じような形であること。
| 5.三年の指導 |
二年から三年にかけては,次に述べる数量関係についての理解を深めるとともに,上に述べた理解をいっそう深め,一次の関係などについても,その中に比例を見いだすことができるようにし,比例という概念を用いて,思考を簡潔にできることを理解させていくがよい。こうした理解を深める機会としては,税金の計算や平方根の用い方などがある。
以上を要約すると,比の指導においては,基準が何であるかを明らかにして関係を考えること,および,基準量・比の値・比で表わされた量の,三者の間の関係を理解させ,これをいろいろな問題に用いていくことなどが重要なことであるといえる。
Ⅱ.数量関係
(ここに数量関係としてとりあげたのは,いくつかの決まった数量を比較した場合の大小相等の関係と,いくつかのいろいろな値をとりうる変量の間の函数関係とをさすものである。)
A.数量関係をみることの長所
ものを比較するときに,比較しようとする性質について基準となるものを定め,基準との関係を数に表わすようにすると,その結果はだれにもわかりよいものになる。
(2) 函数関係についての長所
いくつかの数量の間に,いつも成り立つような一般的な対応の規則を明らかにすると,それらの量についてのいろいろな問題の処理が,やさしく,しかも能率の上がるようにすることができる。
| 1.比較の方法の理解 |
| 2.対応を用いる原則 |
いくつかの数量が互に関係して,いろいろな値に変化している場合には,そのうちの一つの数量の値を一義に決めるために必要な数量が,何と何であるかを考えて,これらを対応させ,次に,その対応している数値の関係をグラフや式に表わしていけば,一般に成り立つ規則が見つけやすくなる。
| 3.変量による考察の原理 |
二つの量がいろいろな値をとりながら対応しているときに,一方の量が他方の量にどのように影響しているかを明らかにするには,一方を一定の順序に変化させ,これを独立の変量とみ,他方をそれに対応する変量として,独立変量の変化の順序に従って比較していくとよい。
C.数量についての指導
大小や相等の関係を変化しない二量について考えることは,すでに小学校で終っているとしてよい。ただ,この場合に,いつも基準となるものを明らかにすること,および基準にとるものが両者で違っているときは,基準をそろえること(これは,比のときに説明したことである)に注意していけばよい。そこで,二量が変量である場合について,次に述べる。
| 1.変数・変量の考え |
変量や変数の考えをはっきりとりあげて指導するのは,中学二年からの仕事であるが,中学一年のときには,その素地になることとして,次のようなことを理解するように指導することが必要である。
(2) 物の代価・仕事の量など,日常に必要となる数量の値が,どんな要素によって決まるかを理解すること。
(3) 和の形になる量は,各項が決まれば決まる。また,積の形になる量は,各因数が決まれば決まること。
また,二年になって,比例や反比例の関係を考えるときに,変量による考え方が生れてくる。
| 2.一次の関係 |
そして,三年になって,この考え方は,文字を用いて表わした公式を,単に数値を計算するためだけでなく,二量の関係としてみるようになって,いっそう伸びていく。
この場合,主としてとりあげるのは,一次式で表わされるような関係である。これについては,次のようなことが理解されればよい。
(2) 一次の関係では,変化率が変らないこと。
(3) 一次の関係は,グラフに表わすと直線になり,比例定数によって,直線の傾きが決まること。
A.表・数表およびグラフの長所
なまの資料から法則や傾向を明らかにするには,それにふさわしい表やグラフにまとめてみると,見通しがついて,明らかにしようとする点が明確になる。
(2) 計算のかわりに用いる表やグラフ
くり返して起る同種の計算は,表やグラフにまとめておくと,いちいち計算をくり返す手数が省けて便利である。
| 1.表の理解 |
表は,実験・実測・調査などによって得た数値をひとまとめにしたもので,次の特徴がある。
(2) 項目の配置をくふうすれば,数値を記録することが能率よくできるし,数値の変化から数量的な関係が明確になる。
| 2.数表の理解 |
数表は,特殊な函数関係を数値によって示したもので,そのもとになっている函数の性質によって,表に出ていない数値についても,表を利用することができる。
| 3.グラフの理解 |
グラフは,資料の数値を図形の大きさにおきかえたもので,次の特徴がある。
(2) 表に比べて,一つ一つの数値は,正確には示せない。
| 4.表・グラフの用い方 |
表もグラフも,ある約束に基いて関係を表わしたものであるから,この約束を守って用いないと,明確な表現とはならない。
C.表・数表およびグラフの指導
| 1.表の指導 |
小学校では,表を読んだり作ったりすることについては,簡単な二次元のものについて,自由にこなせる程度にまで指導されているとみてよい。
すなわち,表が数値の記録や比較に便利なものであること,二次元の表で必要な数値をどのように見いだすかの方法,二次元の表を作るときに気をつけるべき事項などは,だいたいの生徒はわかっているものとしてよい。
中学校では,与えられた表(たとえば,年鑑などにある統計表)を自分の目的にかなうように作りかえたり,表から傾向を読み取ったりすることに指導の重点をおいてよい。
| 2.表についての復習の要点 |
小学校の復習をしている間に,ます,次のことを明らかにしていくがよい。
(b) もとの項目の分類がくわしすぎて,かえって全体的傾向がわかりにくいときには,少数の大きな分類項目にまとめ直す。
(c) どれくらいくわしい数値が必要かを考えて,数値をまるめる。必要な程度の正しさをもつように単位をそろえる。
(d) 必要があれば,もとの数値から差や比を求めて,表に加える。
(e) 必要に応じて,総計や部分計を計算する。このことは,もとの表の数値をそのまま引用する場合には,検証の役目も果す。
(f) 自分の作った表には,次の点を明示して,他の人にわかりやすくする。
(ⅰ)見出し (ⅱ)調査年月日 (ⅲ)数値の単位(ⅳ)調査機関 (ⅴ)出典 (ⅵ)備考
(b) 一方が数量でないときでも,目的から考えて,項目の配列の順序をくふうすれば,関係がわかりやすくなるし,その表を用いる人にも便利になる。(たとえば,統計年鑑のように,いろいろな人の使用の便に供するものでは,都道府県には一定の順序をつけている。また,各地の気温を比較するようなときには,緯度の順に並べる。)
| 3.中学一年の指導 |
このような復習とともに,二次元の表では,縦に数値の変化を見ていって傾向を見いだすこともできるし,横に数値を見ていって傾向を見いだすこともできること,すなわち,縦どうしの傾向を比較することもできるし,横どうしの傾向を比較することもできることを理解させるがよい。
そして,一年の指導では,資料から差や比を求めたりして,このような傾向を発見することに主眼をおき,縦横に項目を配列することが,傾向を条件づける要因を分析していることになることを理解させていくがよい。
| 4.中学二年の指導 |
二年になって,数値のくわしさや正しさに対する見方がはっきりしたころ,あるいは,その前において,数値の信頼性を示すのに,—,?(),0などの記号が用いられていること(普通,—は,そこに該当するものがないこと,0は,実際に数値が0であるか,または無視しうるくらいに小さいことを示す。?は,数値の信頼性が他の数値より劣ることを示す。)や,表中の数値は,多くは近似値であるから,個々の数値の総計と表にある総計とは,少しは違いのあることがあるということを理解させていくがよい。
なお,数値を縦横に配列するとき,その間に,けい線をあまりいくつも入れると,かえって見にくくなるから,けい線をとっても,縦横にきちんと数字が並ぶようにし,数値が5個ぐらいになるごとに間をいくらかあけるようにするなど,見やすくする上の注意も必要なことである。
| 5.特殊な函数関係を示す表 |
計算の手数を省くために用いる表についての指導は,次のようになる。
一年ないし二年では,換算の計算のように,日常くり返し必要になる同種の計算については,その結果を表にしておくことによって,いちいち計算する手数が省けいること。このような例として,旅客運貸・複利表・税額表などがあること。比例の関係にある二量についての表では,表にある数値aと位取りだけが違う数値bに対する数値b’は,aに対する数値a’の位取りを同じように変えて求められること。換算の表では,十進法をもとにした誘導補助単位についての換算にも,上と同じようなことができること。これらのことを理解させるがよい。
さらに,三年になって,一次の関係や比例の関係がもっと問題になってくるときに,一次補間の方法(比例部分)が適用されること,およびその他の関係の場合にも,連続した二量の差があまり変らないときには,近似的に一次捕間(比例部分)が用いられることを理解させるがよい。
そして,この理解と平行して,平方表・平方根表の使い方として,もとの数の位取りと平方あるいは平方根の位取りとの関係を理解させ,平方表・平方根表がさらに広い範囲に適用されることを知らせ,その能力をうるようにすることが必要である。
| 6.グラフの指導 |
小学校で指導されているグラフとしては,絵グラフ・棒グラフ・折れ線グラフ・円グラフ・帯グラフおよび正方形グラフなどがある。
中学一年では,これらのグラフの作り方を復習するとともに,そのおのおのの特徴やグラフ・表のそれぞれの長所を明らかにして,いっそう合目的的にグラフを用いて,いろいろな数量関係を明らかにしていくようにすることがねらいである。そして,これらのグラフを適当に組み合わせて,より複雑な関係を分析していけるようにしていくのが,一年から二年にかけての主要な仕事である二年から三年にかけては,グラフが函数関係を表わすものとして,しだいに函数概念の理解に役だたせつつ,函数のグラフについての理解を深めていく。
| 7.グラフについての小学校の復習の要点 |
小学佼の復習としては,まず,次の事がらを明らかにする。
(b) 絵グラフは,数値の大きさを合同な単位図形を一列に並べたときの個数で示したもので,異なる種類の数量の大小や比による比較に便利である。
(c) 棒グラフは,数値の大きさを棒の長さに変えたもので,数値の大小や比による比較に便利である。
(d) 絵グラフは,異なる種類の数量の比較に便利であるが,棒グラフは,同じ単位で測られた同種の数量の比較にしか使えない。
(e) 棒グラフおよび絵グラフでは,グラフで表わす量を配列する順序をくふうして,項目の違いによる数値の変化がはっきりするようにすることが重要である。
(f) 折れ線グラフは,折れ線の上がり・下がり・こうばいによって,数値の変化の傾向を見やすくしたものであって,棒グラフの頂点を次々に折れ線で結んだものとみられる。(棒グラフの頂点を線でつないだとき,いつも必ず意味のある折れ線グラフになるとは限らない。その線の上がり下がり,こうばいが意味を持つとき,いいかえると,棒グラフの配列が一定の意味のある順序になっているときでなければ,棒のあたまを結んでも意味がない。)
(g) 折れ線グラフは,両軸ともに数量の場合にのみ用いられるが,棒グラフは,一方が数量でなくともよい。
(h) 折れ線グラフでは,こうばいが急なほど変化が大きく,こうばいが右上りならば増加し,右下りならば減少する。
(i) 円グラフ・帯グラフ・正方形グラフは,いすれも,全体に対する部分の関係および相互の関係を,図形の面積に置き換えて示したものである。
(j) 円グラフ・帯グラフ・正方形グラフでは,全体の量がわからなければ,それらがかけない。(各部分がわかっているときは,その合計がひとつの全体としての意味を持ち,しかも各部分の数値に重複や不明のない場合に用いる。)
全体がわからない場合の部分部分の比較には,棒グラフと折れ線グラフを用いる。
単位になる量や軸を決めたあと,量の数値に対応してグラフの点や図形をとることは,円グラフを除いては,だいたい小学校でできているものとしてよい。主として指導すベきことは,単位のとり方,軸の決め方などの,実際にグラフをかく前に考慮すべき事がらである。
単位の大きさや軸の位置は,全体の見ようとする傾向がはっきり浮き出るように,しかも,数量が読みやすいように選ぶことが必要である。すなわち,
また,単位の端下は,1/2,1/4などの簡単な単位分数をもとにしてまとめ,単位図形にもこの端下が読めるようにしるしをつける。
(b) 棒グラフ・絵グラフでは,最大の数値をどれだけの長さで示すかを考えて1目盛の幅を選び,紙面を有効に用いる。また,1目盛に当る量は,絵グラフの単位図形の量を決めたと同じ考えで決める。
(c) 最小値と最大値の差が数値の大きさに比べて小さくて,比較が見にくくなるときは,最小値より下の部分を適当に省略し,最小値と最大値の間の部分が細かく示せるように目盛を決める。(このように,下の部分を省略したときには,![]() 線などを入れて,見まちがわないようにしておく。また,このときは,数値の比を見ることはできない。)
線などを入れて,見まちがわないようにしておく。また,このときは,数値の比を見ることはできない。)
また,棒グラフで,数値の差が大きく,最大の数値を紙面いっぱいにとっても,他の数値がほとんど0にみえるようなときは,大きな数値のほうを分割して平行な棒をいくつも並べ,小さいほうの数値も読めるように目盛をとることがある。しかし,このような場合にも,できれば大きいほうの数値を,いくつかの内訳で示せるようにし,平行な棒をいくつも並べることを避けるようにくふうするがよい。
(d) 円グラフ・帯グラフ・正方形グラフは,百分率をもとにしてかく。あまり小さくて図にかけない項目に対しては,それらをいくつか合わせて一つの項目に作るか,「その他」の項目にするほうがよい。
(e) 必要に応じて,総計や各部分の百分率を記入したり,目盛をつけたりしておくことがある。
(f) 項目の順序は,重要さや大きさの順にかくのが普通である。その他の項目は,いつもいちばんあとにする。(円グラフで,項目の順序は時計の12の位置から,針の回る方向に,順にするがよい。)これらとともに,グラフの軸や線の説明をつけたり,見出し,出典・調査年月・調査機関などの必要な注意を記入することもたいせつである。
| 8.柱状グラフの指導 |
一年から二年にかけて,棒グラフからさらに進んだものとして,柱状グラフが必要になることが多い。これらについての理解は,次のようなものである。
(2) 連続したいくつかの階級に応ずる棒の面積の和は,それらの階級を合併して一つの階級とみた場合の度数を示している。
(3) グラフの山が一つで左右対称に近いときは,平均値は山の頂きに当る階級の近くにある。
| 9.さらに進んだ指導 |
このようにして,一つ一つのグラフの用い方が明らかになるにつれ,これらを組み合わせていっそう複雑な関係を表わしていくようになる。
これについての理解は,次のようなものである。これを指導するのは,一年の中ごろから,三年・三年にわたっている。
(2) 折れ線グラフでは,もとの資料に当る点を結んだ線をもとにして,資料になかった中間の値を推定することができる。
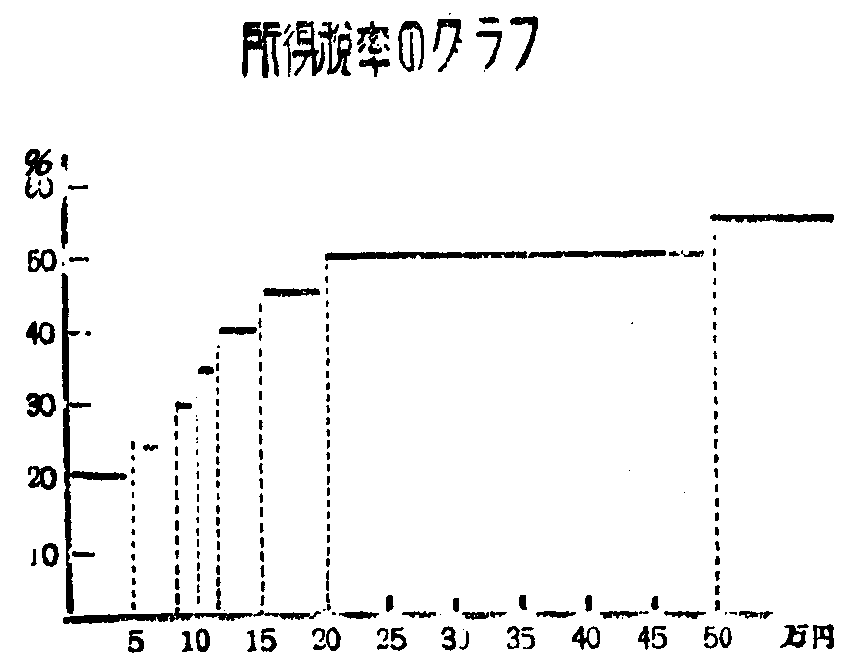
(3) 料金の率や税率のように,階級分けをして,それに応じて決めた値をグラフにかくと,階段状のグラフができる。このとき,階段のどちらの端が意味があるかを明示するには,次のページに示したグラフのように,意味のあるほうの端から横軸に垂線を下したりするとよい。
(4) 徐々に変化する量をグラフに表わすと,なだらかな曲線になるはずである。折れ線になるのは,そのうちの特定の量をとってかいた結果である。
(5) グラフの横軸や縦軸にとった数量が負の値もとるときには,この軸を延長して,負の目盛を反対の方向につけていくことによって,正負にまたがる変化を統一して表わすことができる。
(6) 折れ線グラフの軸は必ずしも0のところにとる必要はない。変化の基準になるところにかいてよい。
(7) 一次式や比例の式など,簡単な式で表わされる数量の関係を示すグラフは,規則正しい直線や曲線になる。
実験などによって得た数値のグラフが,この形に近ければ,その数量の間には,グラフがその形になるような式で表わされる関係があると推定できる。
(8) 資料から得た数値をグラフに表わして見いだした傾向は,そのグラフを延長した部分にも当てはまるとは限らない。このような補外を行うときは,傾向が変らないという仮定が必要である。
| 10.座標の概念 |
このようにして,函数のグラフにまで理解が高まるときに,これに座標の概念が裏付けになっていることを理解させるがよい。
すなわち,表の読み方もグラフの読み方も,横・縦の直交軸を基準にして点の位置を決めていること。また,その他の場合にも,このような点の位置の表わし方が用いられていることを理解させ,正・負の数を用いることによって,平面上の点が座標によって一義的に表わされることを理解させる。これをもとにして,平面上の直線が,また,一つの式で表わされるという,これまで函数のグラフとしてみてきたものに,逆の方から意味づけを行って,式・座標・グラフの結び付きを理解させるがよい。
§6.代数的表現
A.式による表現の長所
数量的な傾向や法則,あるいは数や量についての相等の関係を式を用いて表わすと,次のような利点がある。
(2) 機械的に計算できるように法則や関係がまとめてあるから,必要な結論をうるための思考を,そのままはっきり示しつつ,能率よく運ぶことができる。
| 1.文字の表わす意味 |
(2) 文字は,普通の数と同じように取り扱って,計算の対象とすることができる。
(3) 異なる文字は,異なる対象を表わす。
| 2.等号についての理解 |
等号は,用いる場合によって,次のような意味の違いがある。
(2) 左辺の式と右辺の式の文字に,問題の条件の許す範囲でどんな数値を代入しても等しくなる場合には,等式は計算についての恒等的な関係を法則として表わす。
| 3.数量の間の関係を表わす式 |
公式は,ある数量が他の数量の値からどのように計算して求められるかを,計算式で一般的に示すことによって,数量の関係を表わしたものである。
| 4.方程式の意味 |
方程式は,特定の場合だけに成り立つ相等関係を等式で示すことによって,式中の文字のとる値を条件づけたものである。
C.代数的表現についての指導
| 1.数量の関係を表わす式についての指導 |
ある特定の量が他の量とどんな演算の関係で結びついているかを,数値を用いて式で示すことは,小学校で指導されている。
すなわち,問題解決の過程をそのままに表現するために,計算とは別に式を書いて,明らかにすることが指導されているわけである。そして,この場合に,かけ算やわり算が,加え算や引き算よりさきにする規約になっていることも,理解されているはずである。
中学一年では,このことの復習から始まって,その関係を特定の数値を用いず,その数値が表わしている量を示すことばを用いて表わすように指導する。すなわち,求積や損益の計算などで,同じ演算で解決される問題の解き方を,文章でいうよりも,縦×横のような演算の記号で結び付けた表わし方を用いるほうが簡単であることを,いろいろな機会に指導していくのが一年の仕事である。
そして,その際に,次の点に注意を向けて,はっきり理解させていくことが必要である。
次に,このような式を一度作っておけば,そのあとは,必要な数値の計算は機械的になるので楽であり,また,その関係を人に伝えるにも便利になることを明らかにするがよい。
(2) 中学二年の指導
中学二年では,数値をローマ字で表わして公式をかいたり,その公式を用いたりすることが指導される。この場合に新しく理解することは,次のことである。
(b) 商の記号÷は,特に必要な場合のほかは,それを用いないで,分数の形で表わす。
(c) 各文字がどんな数量を表わすかをはっきり断っておく。なるたけ,同じ種類の数量には同じ文字を用いるようにしたほうが,式の意味を理解するのに便利である。
(3) 中学三年の指導
二年から三年にかけては,文字を用いて関係を表わすことが,次のような利点を持っていることを理解させていくがよい。
(b) 式の中の,ある一つの文字を未知数と考え,他の文字を既知数と考えると,公式は一つの方程式とみられる。したがって,それを解けば,未知数と考えた量を表わす公式が作れる。
(c) ab,a/b,a+bなどのように文字で表わされた数量は,それ自身,一つの数のように考えて計算していくことができる。(a×b,a÷bのように表わしておくと,これは,計算のしかただけを示すほうが主になる。a+bを一つの数のようにみなすとき,(a+b)のように,かっこが用いられる。)
(d) 式中の文字や項を一つの変数とみると,公式は,それらの変数の間の対応の関係を示したものとみることができる。
(e) 上のように考えれば,比例・反比例,一次の関係というような対応のしかたの特徴は,公式の式の形だけからつかめる。(数量の内容を考えずに,式の形だけからわかる。たとえば,y=axの形のときは,yはxに比例する。)
(f) 変数として考える数量をx,y,zなどの文字で表わし,変数とみない量をa,b,cなどで表わして区別して用いると,関係がはっきり示せる。
| 2.式の計算の指導 |
公式や方程式を用いていく過程において,式を計算することが必要になる。式を計算するというのは,式を期待する形のものに変形することであり,期待する形としては,多くの場合,最も項の数の少ない形にすることが普通である。
この計算における理解事項としては,数計算の場合と,どんなことが同じで,どんなことが違うかを知ることが中心といえよう。
中学二年では,さきに述べたように,式の規約としての乗・除の表わし方,かっこの用法,および計算の順序などを知るわけである。そして,式の計算においても,この規約がいつももとになっていること,すなわち,式を計算するときも,文字を数と同じように考えて,乗除の順序やかっこの使用が行われることを指導することが必要である。
このことから,式における項の意味が生れてくる。すなわち,文字や数について,乗除の計算で結び付いた一かたまりが,加・減の対象となることをまず理解することが必要である。そして,同じ文字因数を持った項は,同じ単位を持つ数のように,その数係数についての加減ができること,および,異なる文字因数を持つ項は,それ以上簡単にならないことを理解させ,同類項の計算になれさせることが,式の計算としての第一歩であろう。
次に,式についても,分配や結合の法則が成り立つことをもとにして,かっこをはずしたり,くくったりすることなどの指導に移るがよい。このときに注意すべきことは,係数としての1および0についてである。係数1は,特別の場合のほかはかかないこと(1・x=x),係数が0のときはその項は0であって,これもかかないこと(0・x=0)をはっきり理解させないと,式の計算が困乱する。また,負号を前にしたかっこの式をはずすときに,符号の誤りをしやすい。これも−(a−b)=+(−1)(a−b)と考えて,まちがえないような癖をつけていくことが必要である。
文字式の乗除についても,根本は上と同じことで,そこに適用する数の法則が指数法則であることを理解されればよい。このときも,指数1について,特に注意して指導することが必要である。(a1=a)
| 3.恒等的な関係を表わす等式 |
計算のもとになる結合・分配・交換などの法則や,等式の持つ性質などを簡潔に表わすためにも,等式が用いられる。
この等式として指導されるものには,結合・分配・交換の法則,指数法則,二乗公式および和差の積の公式などがある。これらについての理解事項としては,
(2) このように関係を表わしておくと,これをもとにして,計算の筋道をはっきり説明したり,簡便な計算の方法を考えたりするのに都合がよいこと。
| 4.文字を用いる際の生徒の誤りやすい点 |
このことに指導の手がぬけると,たとえばa%を式中に用いるとき,a/100とせす,aのまま用いたり,.0aしたりする。
(2) 十の位の数字がx,一の位の数字がyである数は,10x+yとなる。これをxyとかく誤りをしやすい。
(3) (xy)2とxy2,3xと3+x,![]() と3×1/2,2倍と2乗などは,混同しやすい。
と3×1/2,2倍と2乗などは,混同しやすい。
(4) 単位を表わす略記号と,量を表わす文字とを混同することがある。印刷のときは,イタリックと立体とで,活字を区別している。
| 5.方程式についての指導 |
方程式の考え方として,未知のものをわかったものの如く考え,わかったものとの関係を等式にかいて,未知のものを条件づけることは,小学校では,逆算として,除法や減法の意味を考えるときに指導されている。(すなわち,□×8=40のような表わし方で,除法を考えた経験はもっているものとしてよい。)
こうした考え方を,公式などを利用するのに積極的に用いたりして,方程式という概念がはっきり取り上げられるのは,中学二年である。中学二年以後の指導においては,このような考え方で,未知の数量についての条件を等式にかくこと,およびこの等式を数値の計算の関係を示すものとみて,機械的に解けるようにすることの二つに,指導の重点が置かれる。
| 6.方程式のたて方の指導 |
方程式のたて方の指導としては,方程式の意味の理解(方程式は,文字が特別の値をとったときにだけ成り立つ等式で,この等式が文字のとる値に条件を与えていること)と,何を未知数として,どのように方程式をたてていくかという方法についての理解とがたいせつである。
そして,後者については,次のような順序で考えていくことが,一般的にいって能率がよいことを理解させるがよい。
(2) その関係を,その文章のままで式にかいていくのには,どんな数量を未知数として,文字で表わせばよいかを考える。
(3) 方程式で相等関係を表わしたときには,両辺の各項は,同じ単位の量を表わしている。
三年になって,上の(2)については,さらに文字(未知数として一つの文字ばかりでなく,二つの文字を用いることもあること,および,文字の数を少なくするよりも,文字の数を多くしても,条件を式に表わすことが簡単になるように考えていったほうが,考えを進めていく上に楽であることなどを理解させるがよい。
同時に,これらの指導を通して,方程式で表わされるのは,問題の数値の間の相等関係だけであり,その他の条件は表わされていないこと,したがって,ある場合には,方程式だけでは問題の条件を尽していないことがあることを理解させ,方程式を解いて得た答を,さらに,検討して,問題の答とするような習慣をつくることも必要である。
| 7.方程式の解き方の理解 |
方程式は,思考を形式的機械的にして,思考過程をだれにもわかるようにし,しかも,楽に進めていけるようにするためのものである。したがって,その解法も,だれにもわかる原理に基いていること,しかも,その原理の適用が機械的にできるようなものにすることが解法としての重点である。
逆算による解き方から等式の性質を利用した解き方へ,さらに移項による解き方へと指導していくときには,いつも,あとの考え方が,前のものより,いっそう計算を進めるのに形式的で,楽になっていることを確認させることがたいせつである。
それとともに,複雑な形の方程式に対して,一般にどんな順序で計算を進めていくかの方針を理解させ,一つ一つの方程式については,できるだけ計算が機械的になるように心がけていくがよい。
根の確め方についても,上の解法の原理が,いつも同値な関係をたどっていることを考えさせ,代入して等号が成り立たないときに,そこからあとの計算に誤りがあることを理解させるがよい。
グラフによる解法は,根が近似値でよい場合や方程式の意味を考える場合には便利であるが,正確に能率よく根を知るためには,あまり便利でないことをよく理解させる。また,グラフを手がかりとして,二元の方程式の意味にはいっていくことは,わかりよい方法であろう。
二元の方程式では,方程式一つでは未知数が決まらず,二つの未知数の間の対応関係しか決まらないこと,および,これが二つあるときにはじめて,二つの未知数が決まることを理解させる。こうして,二元方程式を解くことの意味の理解を確立することが,まず,必要である。その解法については,消去の意味や消去のための機械的な方法としての加減法を理解させればよい。
D.指導上の注意
たとえば,2x+3=x+5
=2x−x=5−3など
(2) 方程式を解いた場合に,必す検算をする習慣をつけることが必要である。これは,論理的に必要でなくとも,誤りを防いで,確実な仕事をするようにする意味からもたいせつである。
問題解決に方程式を用いたときは,方程式の根がそのまま問題の条件に当てはまるとは限らないことがあるから,論理的にいっても,検算を忘れてはならない。すなわち,物の個数を表わす数が小数として出たり,速さや金額が実際にあり得ないような数となったりするときは,そのまま問題の答とすることはできない。
(3) 方程式を解くときは,いつも,途中の計算の見とおしをつけるようにすることが必要である。
§7.図形による表現(縮図・地図・投影図)
A.図形による表現の長所
物の形・位置・つながりなどを,目的に応じた適切な図を用いて表わすと,ことばでいうよりもわかりよく,他の方法では表わせないような複雑な関係をも,明確に示すことができる。
B.図形による表現の理解
| 1.表現についての理解 |
平面の上の図で,物の形・大きさ・位置・つながりなどを表わそうとすると,そのおのおのの場合の目的に応じた約束や記号が必要になる。
| 2.縮 図 |
平面の上の物の形と大きさは,その形と相似な図形とその相似比とで示すことができる。
| 3.地 図 |
地形は,水平面上で考えた地物の形,および,水平面に平行な一定間隔の平面で切った切り口を水平面へ投影した形の相似形と,その相似比とで示すことができる。
| 4.投 影 図 |
人工物では,互に垂直な部分が多いので,等高線のような方法では,形が示せない。そのため,互に垂直な二つ,あるいは三つの平面を考え,この平面へ投影した形の縮図を,一枚の平面の上に,一定の約束で広げた図面で示すようにしている。
C.図形による表現の指導
小学校では,案内図をかいたり,簡単な縮図や地図で方位・道のりを求めたりすることが指導される。社会科でも,これらのことのほかに,等高線の意味や,等高線の状態と地形の特徴との間の対応が,ある程度までわかるように指導されているとみてよい。
中学校での指導は,これらの背景として,相似の概念が含まれていることを明らかにし,相似の条件から縮図や地図を作っていく方法を理解し,図的表現を,一つのことばとして,自在に使えるようにしていくことがねらいである。この間の指導において,それらの図表示では,何が正しく表現され,何は表現されていないか,どんな約束で表現しているかなどを理解させていくことが重要である。
| 1.小学校の復習の要点 |
まず,小学校の復習として明らかにすべきことをあげると,次のようになる。
(2) 縮図では,建物・田畑などの形や配置が正しく表わされている。また,縮尺を用いれば,図上で測った長さに縮尺の分母を示す数をかけて,実際の長さが求められる。
角や方位は,図上で測った値が,そのものの値である。
(3) 長方形などから組立てられた平面図形は,必要な部分の長さを測り,直角に対応する角をそのまま直角にとって,図上の主要点を決定していけば縮図がかける。このとき,方眼紙を利用すると便利である。
(4) 縮図をかくときには,次のように縮尺を考えていくと,手ぎわよくいく。
(b) 縮尺の分子は1,分母は10,100,1000,10000などか,あるいは,これらの数(位取の単位を示している)の約数になるように決める。
(例 1/200000,1/50000,1/1000など)
| 2.中学一年の指導 |
こうした復習とともに,縮図が地面の上のものを示すだけでなく,人工物の形を示すものとして,断面図や平面図などとして用いられることもあること,また,縮図とは逆に,拡大図も用いられること,これらの場合に,図では示せない重要なものは,いろいろな記号をくふうしてわかるようにしてあることなどを理解させるがよい。
| 3.中学二年の指導 |
中学二年では,縮図を作ったり,縮図を作って必要な部分の長さや角を測ったりすることが指導される。その際の基本的な理解事項は,次のようなことである。
(2) 三角形は,次のものの大きさが決まると,長さは一定の縮尺で縮小し,角は,そのままの大きさにとることによって,それと相似な図形をかくことができる。
(b) 二つの辺の長さと,そのなす角の大きさ。
(c) 一つの辺の長さと,その両端の角の大きさ。
(4) 正確な図面を作るときは,相似比とともに,尺度(てい尺)をつけておいたほうがよい。紙面が縮むと,相似比は役にたたなくなるが,尺度のほうは役にたつ。
| 4.等高線の指導 |
こうした理解をもとにして,相似の概念を実際的に役だつように理解し,用いていくことができるようにするとともに,等高線についても,次のような理解を深めて地図の用い方になれさせ,他の概念の理解の素地を作っていくがよい。
(2) 二つの等高線の間にある点の標高は,その二つの等高線の高さの中間にある。
(3) 二つの地点を結ぶ直線のこうばいは,その二点の標高差の水平距離に対する比の値で表わされる。
(4) 等高線の密なところは,こうばいが急である。
| 5.中学三年の指導 |
中学三年では,図的表現として,これまで二次元的なものしか扱わなかったのを,三次元のものにまで押し進めていく。すなわち,平面図や断面図などで示した物の形の表わし方を発展させて,投影図にまとめていくのである。そのときの理解事項としてたいせつなことは,次のことである。
(2) 二つ,または三つの画面を使う理由
(3) 地図・縮図との異同(地図は地表の凹凸を等高線で示しているが,人工物では等高線で示せないものがあるから三画面を用いる。)
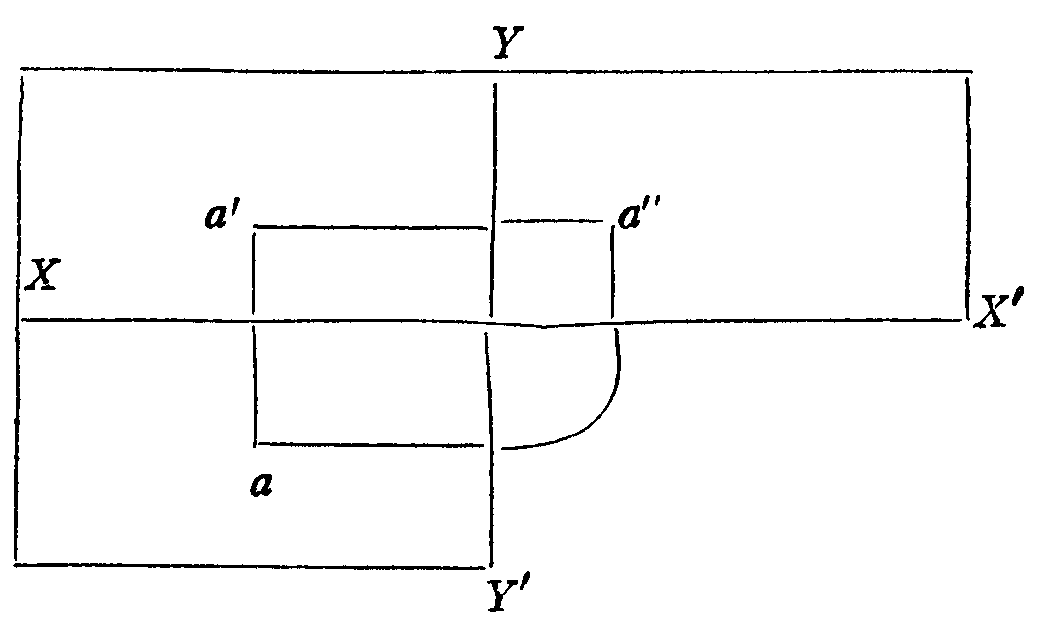
(4) 一点Aの平面図,立面図,側面図を,それぞれa,a’,a''とすると,aa’は平面図と立面図の境の基線XX’に垂直で,a’a''は立面図と側面図の境の基線YY’に垂直である。そして,aとXX’の距離は,a''とYY’の距離に等しい。
(5) 画面に平行な直線の長さは,その画面に正しく表われている。
(6) 画面に平行な二直線のなす角は,その画面に正しく表われている。
(7) どちらの画面にも平行でない直線の長さやそのなす角は,画面の上にはそのままでは現れていない。
(8) 回転体・対称形・柱状体などでは,示さなくともわかる部分の図面(たとえば,対称面の片側,柱状体の側りょうの方向)は省いてよい。
この指導に当って,実際の技法については,図画工作科の指導とよく連絡することが必要である。
D.指導上の注意
(2) 図には,その目的に照らしていらないものは,無視してかいてある。その無視したものまで,その図から判断してはならない。
(3) 図をつくるときには,ぜひ表わさなくてはならないものは何か,何を無視するかなどをよく考えてから,次に概形をとらえて,かいていく手順を考えるがよい。
(4) 1/3,1/6,1/7などのように,分母が10,100,1000,……などの約数でない数を縮尺にとらないようにする。
§8.簡単な図形
A.図形の長所
日常に用いている物の形や位置関係には,その物を使う目的に応じて,美しさ・安定性・扱いやすさ・作りやすさなどの点で,何らかのよい点をもっている。そして,そのよいところは,図形についての簡単な数量的な関係に基いている。
B.図形についての理解
| 1.関係のとらえ方 |
いろいろな図形や図形の間のいろいろな関係は,図形を組み立てている点・線・面の結合しかたや位置の関係あるいは,線の長さや角の大きさの関係で,特徴づけることができる。
| 2.図形の分解 |
複雑な図形について,その性質を調べたり,これをかいたりするときには,その目的に応じた簡単な基本図形,(たとえば,性質を調べるときには三角形,長さ・面積などの計算のためには正方形や直角三角形など)に分解して,調べやすい部分になおしていくことができる。
| 3.平行・垂直の理解 |
直線や平面の間の平行・垂直の関係は,物の形をきちんと組み立てたり,長さを測ったりするときのもとになる。
| 4.合同・相似の理解 |
図形の形を区別したり,実際にあるものを模写したりするときは,合同や相似の条件によって,そのものを構成している直線や角の関係をもとにすればよい。
| 5.美しい形 |
きちんとまとまった単一の図形やそれを一定の規則で配列した図形は,美しい感じを与える。そして,これらの図形の特徴は,その角や辺の間の関係や合同・相似などの関係によって,とらえることができる。
| 6.直角三角形 |
直角三角形の辺や角の間には,簡単な式で表わされる関係がある。この関係を利用して,必要な長さや角を,計算によって,正確にしかも能率よく求めることができる。
C.図形についての指導
図形についての指導では,いろいろな図形や図形の間の関係を見いだし,それをもとにして,実際の問題を解決していくことをねらうのが中学校での仕事である。図形について論証の性質を明らかにすることは,高等学校での仕事である。
小学校では,直観的に立方体・直方体・円・長方形・正方形・球などの図形を見いだし,他と区別することや,平行・垂直を直線どうしの組について見いだすことが指導されている。中学校では,これらのものについて数量的な特徴づけをして,そうであるものとないものとを,測定によって区別できるようにするという点で,小学校の扱い方より論理的になるが,公理などを設けて,それから証明するということは考えない。
| 1.平行と垂直の関係についての指導 |
どんな場合に平行や垂直ということばを用いるかは,小学校ですでに指導されている。中学校では,これらのことの復習から始めて,次のことを理解させる。
(b) 水平な平面,水平な直線,鉛直な平面,鉛直な直線の間の関係。
(c) 平行線・垂線を,分度器・定木・コンパスなどで作るために必要な平行線・垂線の性質,およびこれを利用した作図の方法。
(d) 長方形・直方体(正方形・立方体も含む)にみられる平行・垂直の関係。
(e) 二組ずつ平行・垂直の関係にある三つの直線または平面の間の関係,たとえば,a//b,b//cならば,a//cなど。
さらに,平行や垂直をもとにして図形を考えていくときには,図形として,直角三角形や長方形が生れてくる。これについての指導は,以下の学年で行われる。
(2) 中学二年の指導
垂線を下したりして図形を分解していくことは,図形についての計量を行うときの有効な方法である。すなわち,中学二年では,これに関して,次のような理解事項が新しく加わる。
(b) 三角形・平行四辺形・台形の面積の公式。
上の考え方の発展として,中学三年では,三平方の定理や三角比の用い方が指導される。すなわち,
(b) 一つの図形を,二辺の長さが容易に測れるような直角三角形に分解していくことによって,いろいろな部分の長さを計算して求めることができる。
(c) 直角三角形では,その一角と一辺とがわかっていると,三角比の表を利用して,他の辺の長さを求めることができる。また,二辺がわかっていれば,その角も求められる。
(d) cを直角三角形の斜辺,b,aを直角をはさむ二辺,Aをaに対する角とすると,次のようになる。
a=c sinA,b=c cosA,a=btanA
| 2.いろいろな形の名まえおよび合同・相似についての指導 |
小学校では,図形の名前として,三角形・長方形・正方形・円・直方体・立方体・球などを知っている。
中学一年では,さらに,二等辺三角形・正三角形・直角三角形・鋭角三角形・鈍角三角形・台形・ひし形・平行四辺形・正多角形・円柱・円すい・角柱・角すいなどの名前を知っていくわけである。このときの理解事項としては,それらの,形が他のものとどんなことで区別されているかを知ることであり,その目のつけどころが,長さや角の関係や,線と面とのつながり方であること,および,このような関係でとらえておけば,それらの形を作るのに,測定を利用できるので便利であることを知らせるがよい。
そして,見たところ同じ形のものには,同じ名前がついていること,形として同じであれば,大きさが違っていても,同じ名まえをいうことに注意を向け,相似の概念に発展する素地を作っておくがよい。
(2) 中学二年の指導
中学二年では,上のことを確認し,同じ形ということを数量的に条件づけて,相似の概念を理解し,同じ図形ということを数量的に条件づけて,合同の概念を理解させることが中心の問題である。
こうして,相似や合同の意味が明らかになると,これを実際に適用するために,特定の図形についての合同・相似の条件が問題になる。ここで,三角形についての条件がすべての根底になることを,Bにあげた理解の2に基いて理解させ,これをいろいろな場面に応用させるがよい。さらにこの発展としては,円や同じ辺数の正多角形はどれも相似形であること,長方形・円柱・円すいなどは,その二つの要素で,形が決まることなども理解させるがよい。
(3) 中学三年の指導
中学二年から三年にかけては,次のような指導が必要である。すなわち,合同なものを作ることが大量生産の方法であることや,相似をもとにしてわれわれが形を人に伝えていることなど,合同・相似のよさを明らかにする。さらに進んで,相似形の長さ・面積・体積の関係を明らかにし,これに基いて,円・球の求積公式の理解を深めることも必要である。また,相似形の性質を利用した縮図や拡大図の簡便な書き方をくふうすることも意味がある。これらのことから,相似の位置や相似の用心についても理解させたらよい。
また,合同の概念やその条件についての理解を深めていく機会としては,二等辺三角形の性質や,垂線・二等分線・垂直二等分線などの作図がある。こうした学習を通して,図形を分解してより簡単なものに帰著させていくと,考えよいことを理解させるがよい。
展開図を展開するにも合同の考えは必要である。すなわち,平面で囲まれた形を展開するときは,各面が,合同に,一平面上にうつされていることを理解することが必要になる。
また,中学三年では,形の特徴として,回転体や対称形のような見方を学習する。このときにも,合同の概念が指導される。
| 3.形の美しさや有用性 |
形の美しさや有用性についての指導は,前の二者の指導に並行して行われるのがよい。
中学一年では,次のようなことがらを理解させていくとよい。
(b) 直方体や立方体のように,垂直な面で囲まれた物体は積み重ねたときにすき間なく並び,安定性があり,かつ,製作がやさしい。
(c) 正多角形や円のように,まとまりのある図形は美しい感じを与える。
(d) まとまった美しい形のものを平行に配列したものも,美しい感じを与える。
中学二・三年か,さらに,次のようなことが理解されていく。
(b) 単一な図形を相似に拡大・縮小しつつ,一定の比で平行に配列したものも美しい感じを与える。
(c) 面対称・線対称な図形は,まとまった美しい感じを与える。
D.指導上の注意
(2) 三角比や三平方の定理についての指導においても,上のような注意が必要である。実際の場面には,高さに相等する直線も,水平距離に相当する直線もかいてないし,目にも見えないことがおおい。目的に応じてこれらの直線を想定し,不必要な物をとり除いて,直角三角形を取り出すことができなくてはならない。そのためには,教師や教科書によって単純化され抽象化された図形について学習するだけでは,ふじゅうぶんである。
(3) 合同と相似,線対称と面対称のように,類似の概念や,平行四辺形と長方形のように,特殊と一般の関係にある概念についての用語は,これらの異同を明らかにしないと,誤って用いるようになる。この異同を明らかにするような機会を与えるように,指導を計画することが必要である。
(4) 中学校における作図では,正確な実際的な図を作ることが目的であって,定木・コンパスに限らず,分度器やものさしも,自由に用いていくように指導してよい。
§9.実 務
A.実務における数学の長所
おかねは,経済的な価値の尺度であって,正確なおかねの計算によって,経済的な関係を,円滑しかも公正に取り扱っていくことができる。
B.実務についての理解
| 1.バランスの原理 |
ある期間のおかねのやりとりでは,たとえば,収入と支出のように,はいってくるおかねの合計と,出ていくおかねの合計とは,等しくなっている。
| 2.比例の原理 |
おかねを貸借したときの報酬やおかねの生み出す利益は,期間の長さと金額に比例する。
| 3.おかねのはたらき |
(2) 多額の金額を一時に負担するよりも,これを小分けにして負担したほうがらくである。
| 4.信 用 |
おかねは信用をもとにして流通している。このはたらきをいっそう円滑にするために,いろいろな信用制度が作られている。
| 5.記録と計画 |
おかねを有効に,かつ公正に使っていくためには,数量的な記録や計画が必要である。
| 6.指 数 |
時間的に変化していく生産量・物価・賃金などの諸量は,ある時期におけるこれらの量を基準として,他の時期の量を,その基準に対する百分率で表わしておくと,その量を表わす単位に関係なく,量の変化が比較できて便利である。
C.実務の指導
数学科の指導内容として,利率・税・手形などの経済的な事項があげられているのは,次の理由による。
(2) これらのことは,中学校の数学的な指導内容に対して,日常生活における重要な応用面となっていること。
こうした見地から,その根本になることを考えてみると,経済的事項を,加・減の計算にのせていくための基本として,バランスの原理があり,乗・除の計算にのせていくための原理として,比例の原理がある。そして,比例という見方が,ある意味で当てはまらなくなる場合として,上の理解の3であげた事実がある。こうしたことの理解の上に立てば,おかねの計算が気やすく,しかも能率的にできるようになる。また,新しい事がらにぶつかっても,その意味をやさしくはあくしていくことができる。
| 1.小学校との連絡・中学一年の指導 |
小学校では,こうしたことについては,おつりの計算,仕入れ,売買の利益・損の関係,簡単な記帳や予算のたて方,郵便料金,預貯金の手続きなどが指導されている。中学一年では,こうしたことの復習から始まって,そこに割合の考えを取り入れて,もっと関係を明確にしていくことから指導が始まる。
その主な理解事項をあげると,次のようである。
(2) 仕入れ値と売価との差が,もうけまたは損であること。
(3) 預金した金額と利息との合計が,引き出した金額と残金との合計に等しいこと。
(4) 品物を売買したとき預貯金したときなどには,いつも一定の形式の記録のしかたがあり,この記録をとることによって,不正と誤りとを防いでいること。
さらに,中学一年の重要な仕事としては,損や利益がおかねの単位を用いて表わされるだけでなく,もとでに対する割合で表わされることを理解することである。
| 2.売買における実務の指導 |
しかし,これを,40,000円のもとでを持っていて,どちらの品物を扱うのが有利かということになれば,1反800円のほうでは,
400円×50=20,000円のもうけとなり,2000円のほうでは,
400円×20=8,000円となって,前者のほうが有利となる。
この関係はもとでがいくらになったときも同じであって,もとでに対する比率,すなわち,.5と.2とを用いて表わされるのである。
(2) 同じようなことは,割引の場合でも,利息の場合でも,当てはまる。その場合の尺度となる比率が,割引率や利率である。
(3) 利率は,一年とか一月とか,一日とかを基準にして表わす。
| 3.必要な実務についての知識 |
上に述べたような数学面の理解とともに,次のような事がらについての知識も指導されてよい。
(2) 商店は,いろいろな場合に割引をする。この場合には,商人は,品物の売れ行きが平常の時よりよくなることを希望していることを示す。
(3) 一時におかねを払うよりも,月賦などで,分割して払うほうが高いのが普通である。
(4) 銀行や郵便局は,各個人のこまかいおかねを集めて,大きなはたらきのあるものにしている。このはたらきの生み出す利益の預金者への配当が,利息に当る。
| 4.中学二年の指導 |
中学二年では,株式や債券・複利計算について学習するが,この場合に理解させることは,次の点である。
(2) 株式は出資金であり,債券は借用証書であること。債券は,そのおかねをいつか返してくれるものであるが,株式は,返さないのがたてまえである点が違うこと。
(3) どちらも売買できるものであり,売買する値段は,一般に,額面と異なること。
(4) 配当や利息は,額面に対する比率で表わされていること。これらの株式や債券を買ったとき,それによる利益の出資額に対する割合は,普通,上の比率とは異なること。
(5) 複利計算の方法と意味,および,これが長期の融資に用いられていること。
| 5.中学三年の指導 |
中学三年では,いっそう進んだ実務として,小切手・手形についての知識,保険・税についての知識が指導される。この場合に主要なことは,次の事がらである。
(2) 税・保険は,ともに,多額の負担を,大ぜいで小分けにして負担する方法である点で同じである。
(3) 保険料,所得税などの計算の方法
| 6.指数についての指導 |
品物の値段は,時期によって,値上り・値下りがあること,この値上がり・値下がりが生産に大きな影響を与えること,および,これを数量的に明確につかむことが重要なことがらであることは,中学二年ぐらいで理解できることである。こうしたことを理解するものとして,指数を用いる考え方が,中学二年から三年にかけて指導される。
その中心となることは,次の事がらである。
(2) 三つ以上の品物の値上がり・値下がりを比べるには,連比によるよりも,各品物ごとに,基準時の値段に対する百分率を用いたほうが比べやすい。
(3) 指数の考えは,値段だけでなく,生産量・貿易額・人口など,品質の違ったものの変化を比べるときも使える。これは,指数の値が,もとの量で表わす単位に関係しないからである。
(4) いくつかの指数を組み合わせて,一般的な物価とか生産の状態とか賃金の状態とかのような,数量で表わしにくかったものを,指数で表わすことができる。
D.指導上の注意
(2) 利率には期間が指示されている。計算をするときは,その期間を単位として,実際に貸借した期間を表わさなくてはならない。
たとえば,年利6分で,3か月のときは,(元金)×.06×3/12としなくてはならない。
(3) 金銭計算の場合,自分の見積りだけならば概数でもよい。実際の取引きでは,端数の扱いに対して,社会で決めた約束があるのが普通であるから,これに従わなくてはならない。
(4) 歩合・歩合高・元高に相当する用語が,場合場合によって違うから,よく区別するように指導することが必要である。これについては,次の表を参照して,よく知らせるとよい。
歩 合 に 関 す る 実 務 の 用 語
|
|
|
|
|
|
|
| 売 買
割引(売買) 利息計算 〃 株 式 債 券 証券投資 手形割引 税 保 険 |
利益・損
割引高 利 息 利 息 配当(金) 利 息 利 益 割引高 税 額 保険料 |
利益・損の歩合(歩合,%)
割引率(歩合,%) 年利,月利(歩合) 日歩(100円当り…銭厘毛) 配当率(歩合) 利率(歩合) 利まわり(歩合) 割引率(日歩) 税率(%) 保険料率(10,000円につき…何円) |
年,月 日 年 年
日
|
原 価
定 価 元 金 元 金 額 面 額 面 買 価 額 面 課税額 保険金 |
売 価
売 価 元利合計 元利合計 現価(手取り) |