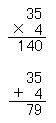第 2 部
特 殊 な 問 題
1.診断的指導
この指導は,算数の数学的目標の主要な部分を占めている技能を,できるだけこどもたちが自学自習して自分の力で身につけたり,また,これを忘れないで,必要に応じていつでも使えるようにするために,考えられた指導の方法である。ここでは,この指導をどんなに用いていくことができるかについて,その主要な点を述べることにする。
(1) 診断的指導の意味
こどもたちは同じような学習の場について,同じような学習活動,練習などをしても,どのこどもも同じようにできるようになるとはいえない。かえって,同じようにならないのが普通であるとさえいえる。このような違いの起るのは,めいめいのこどもの学習の速さ,興味,知能的なはたらき,情緒的なはたらき,肉体的なエネルギー等の個人差によるものであると思われる。
さて,数学的目標の主要な部分を占めている計算について,こどもがその計算のもとになっている原理を理解しても,その原理がもとになっている計算のどれもが,できるとはいえない。
たとえば,よせ算について,そのもとになっている次の原理を,こどもがすっかり理解したとする。
その原理を用いて,やさしいよせ算はできるであろう。しかし,たとえば,原理を何回もくり返し適用していくような計算となると,どのこどもも,正しくできるとはいえない。このような理由から,計算などではその手続の上から,これを単純に適用できるものから,何回も適用するものへと,いくつかの段階に分けて指導することが必要になるであろう。
ここに,よせ算について,その段階を細かく分祈したものの一例をあげておこう。
| 1 |
(基数)+(基数)(加法九々といわれるもの) |
|
2+3, |
7+8 |
| 2 |
(何十)+(基数) |
20+3, |
30+7, |
60+8 |
| 3 |
(何十)+(何十)={何十あるいは百 |
30+20, |
40+30, |
30+70 |
| 4 |
(何十何)+(基数)(繰上がりなし) |
23+4, |
41+8, |
12+7 |
| 5 |
(何十何)+(基数)(繰上がりあり) |
43+7, |
41+9, |
27+9 |
| 6 |
(基数)+(何十何)(繰上がりなし) |
5+24, |
3+65, |
7+42 |
| 7 |
(何十何)+(何十)(同上) |
46+20, |
37+40, |
22+60 |
| 8 |
(何十)+(何十何)(同上) |
30+27, |
40+32, |
60+28 |
| 9 |
(何十何)+(何十何)(同上) |
42+36, |
57+32, |
26+33 |
| 10 |
(何十何)+(何十何)(何十あるいは百) |
26+14, |
78+12, |
46+54 |
| 11 |
(何十何)+(何十何)=(何十何)1の位だけ繰上がる |
47+36, |
35+48, |
38+57 |
| 12 |
(何十)+(何十)=(百何十) |
60+70, |
50+90, |
40+80 |
| 13 |
(何十何)+(何十)={何百あるいは百何十何 |
46+60, |
58+60, |
38+70 |
| 14 |
(何 十)+(何+何)={何百あるいは百何十何 |
30+78, |
20+98, |
10+97 |
| 15 |
(何十何)+(何十何)= |
百何か
百何十何 |
1の位は繰り上がらない |
43+92, |
75+43, |
82+46 |
| 16 |
(何百何)+(何百)=(何百何十) |
450+300, |
280+400, |
620+300 |
| 17 |
(何百)+(何百何十)=(何百何十) |
200+640, |
100+390, |
300+410 |
| 18 |
(何百何十)+(何十)=(何百何十)10の位が繰り上がる |
460+70, |
380+60, |
540+90 |
| 19 |
(何十)+(何百何十)=(何百何十)同上 |
40+580, |
30+280, |
60+470 |
| 20 |
(何百何十)+(何百何十)=(何百何十)繰り上がらない |
260+320, |
240+330, |
620+240 |
| 21 |
(何百何十)+(何百何十)=(何百何十)10の位が繰り上がる |
360+280, |
450+280 |
|
| 22 |
{(何百何あるいは何百何十何)+(何百)}= |
何百何
何百何十何 |
406+200, |
467+300 |
|
| 23 |
(何 百)+{何百何あるいは何百何十何}= |
何百何
何百何十何 |
400+507, |
300+538 |
|
| 24 |
(何百何)+(何百何)=(何百何)繰り上がらない |
306+203, |
403+205 |
|
| 25 |
(何百何十)+(何十何)=(何百何十何)同上 |
570+26, |
530+48 |
|
| 26 |
(何十何)+(何百何十)=(何百何十何)同上 |
35+440, |
67+920 |
|
| 27 |
(何百何十何)+(何十)=(何百何十何)同上 |
437+40, |
648+50 |
|
| 28 |
(何十)+(何百何十何)=(何百何十何)同上 |
70+326, |
80+719 |
|
| 29 |
{何百何あるいは何百何十何}+(何十何)=(何百何十何)同上 |
708+41, |
623+72 |
|
| 30 |
(何十何)+{何百何あるいは何百何十何}=(何百何十何)同上 |
52+406, |
57+721 |
|
| 31 |
(九十何)+(基数)=(百何) |
96+6, |
93+8 |
|
| 32 |
(基数)+(九十何)=(百何) |
9+96, |
7+94 |
|
| 33 |
{何百何あるいは何百何十何}+(基 数)= |
何百何
何百何十何 |
408+6, |
473+8 |
|
| 34 |
(基数)+{何百何あるいは何百何十何}= |
何百何十何
何百何十
何百何
何百 |
7+306,
4+576,
3+497 |
6+347
8+496 |
|
| 35 |
{何百何あるいは何百何十何}+(何+何) 1の位だけ繰り上がる |
108+26, |
264+27 |
|
| 36 |
(何十何)+{何百あるいは何百十何} 同 上 |
46+209, |
37+456 |
|
| 37 |
(何十何)+(何十何)= |
百何
百何十
百何十何 |
1の位,10の位とも繰り上がる |
38+65,
28+73 |
47+73 |
|
| 38 |
(基数)+(何百何十何)=(何百何十何) |
4+578, |
9+673 |
|
| 39 |
{何百何あるいは何百何十何}+(何+何) |
709+97, |
648+54 |
|
| 40 |
何百何
何百何十何 |
+(何百何) |
109+403, |
256+409 |
|
| 41 |
(何百何十何)+(何百何十何)<1000 |
354+467, |
246+564 |
|
以上41段階にくぎったのであるが,これは和が1000以内の場合についてである。
先に述べたように,手続の簡単な二,三の段階ができても,どのこどもも全部の計算ができるとはいえない。診断的指導と言うのは,よせ算について言えば,よせ算の演算の意味や,よせ算のもとになっている原理が理解されたところで,上にあげた段階に従って原理を適用し,できるだけ,こどもの力で進めるところまで進むことができるようにするのである。もしもできないところがあったら,すぐに前にもどって練習したり,原理を思い出したりして,学習を進めていくようにするのがよい。
(2) 診断的指導の進め方
診断的指導によって学習を進めるとして,これに必要な教師の準備と,学習指導の進め方の大要について述べることにする。まず,教師はどんなものを準備しておいたらよいかについて述べてみよう。
その方法上のことについてはあとで述べることにして,ここでは主として,どんな教材・教具を準備しておいたらよいかを中心において,述べていくことにする。
細かに分析した各段階の問題を印刷して,これに裏ばりをして,しっかりとした計算カードを作る。その上に各段階の計算について,こどもが困難を感じたときに,どのように指導するかの具体的な指導の対策をたてておくのである。
たとえば,こどもの中には,加法九々のどれかをまちがえて記憶しているために,誤算をすることがある。このような場合に備えて,加法九々を,自習によって反復練習するために必要なカードを作っておくのである。また,繰り上がる操作がわからないでいるこどももあろう。このようなこどもに対する指導のために,色棒や色おはじきを準備しておき,数の大きさや位取りについての指導をするのである。
また,よせ算の意味についても,計算と同じようなことが考えられるであろう。このために必要な問題も,こどもの身近な生活から,簡単なものから,しだいに複雑なものへと分析して,これを計算のためのカードと同じように,問題カードを作る。
これらは,診断的指導をするために必要な最少限の準備である。
このような準備ができたとして,どのようにして診断的指導を進めるかについて,述べることにする。
例を3年生のよせ算の指導にとって述べてみよう。2年で「よせ算」の意味の基礎と,よせ算九々について指導してあるとする。そこでまず,既往経験をもとにして,こどもの具体的な生活をとおして,「よせ算」の意味やよせ算のしかたについて指導し,こどもがよせ算の原理を理解したとする。そのあとで,実際の場に適用してみたりして,一応計算のしかたについて理解したとする。その次に,診断的指導にはいるのがよい。
教師は用意した診断テストを用いて,こどもの困難なところをさがし出すのである。めいめいのこどもの当面している困難がわかったら,これに応じて先に準備しておいた問題カードを各人に与えて練習させるのである。一つの段階が終ったら確かめをして,完全にできたら次の段階の問題カードに移る。必要があれば,教師の指導を受けて確かめる。このようにして,こどもは,各人の能力に応じて進むようにする。この間に,教師はこどもを観察して,くり返しもう一度練習させるとか,計算の速さを増すようにさせる等,適当な指示を与える。また,困難を生じたこどもを見つけたら,その原因を取り除くように,前に用意しておいた教具等を使って,適切な指導をするのである。このようにして,こどもが自分を診断しながら,順次に困難な計算ができるように指導していくのである。
診断的指導をするときに,よく診断テストを用いる。このテストによって,そのあとでの指導が決まるのであるが,その指導は次の三つの類型に分けて考えることができる。
(a) 学級全体のこどもに,いくつかの段階について,もう一度指導することが必要である。
(b) 同じことに困難を感じているこどものグループに対して,その困難を取り除くための手がかりを与えることが必要である。
(c) 特定のこどもが,あることに困難を感じたり,混乱を起したりしているので,これを乗り越えていくために,基礎的な事項についての学習の手がかりを与える。
(3) 診断的指導をするための準備
ここでは,教師の仕事や準備について注意したらよいと思われる事がらを用いて,どのように診断的指導を進めていったらよいかを,明らかにしてみよう。
(a) 一段階に一つの新しい要素がはいるように,段階をくぎる。
指導しようとする技能を,手続の容易なものから複雑なものへと順序だてて,いくつかの段階にくぎる。(1)の診断的指導法の意味にあげた「よせ算」の例がそれである。
段階をくぎるときに,重要な条件は,原理を適用する際の手続の上で,一段階に一つの新しいものを入れるようにすることである。このように段階をくぎっておけば,こどもがある段階にはいったときに困難を感じたとすると,どんなことがその原因になっているかを,たたちに自分で診断ができるからである。
また,教師の側でも,新しい要素がただ一つであるから,指導を要する点は,どんなことであるかを,すぐに診断することができ,指導の対策をたてることができる。
(b) 当面している困難ごとに,これをいくつかの段階に分析する。
ひき算の原理が理解できたところで,診断テストを用いたら,特に,次の三つに,こどもの当面している困難をまとめることができたとする。
(ⅰ) 全然できないもの
(ⅱ) 被減数に0を含んでいるもの
(ⅲ) 続けて二回繰り下がるもの
この場合に,おのおのの困難に当面しているこどもを指導するために,その困難を克服していくために必要な段階を細かく分析して,こどもが努力しさえすれば,次の段階に進むことができるようにするのである。これなしに指導したのでは,こどもが理解をもって学習していくことができず,こどもに計算方法によって示される行為の形式を,なんらの批判的な思考も用いないで,そのままに教え込んでしまうことになるのである。
(c) 具体的なものを使って,困難を克服していくために必要な,基礎的な概念をしっかり作り上げる。
たとえば,「20−5」のような計算のできないものがあったとする。このこどもに,ただ抽象的に,ひき算の手続を教えてみても,こどもは,ただ,その手続を記憶するだけにとどまって,論理的に物事を考えていくようにはならない。もしも,ひき算の基礎になっているひき算九々をまちがって記憶していたら,どんなにひき算のしかたを指導しても,それはむだである。また,数と記数法との関係,つまり位取りの原理が理解されていなかったら,たとえ,20−5のひき方がわかったとしても,30−7のような計算ができなかったり,その他,いろいろな計算ができなくなるであろう。したがって,教師は困難を起している原因は何であるかを診断して,その診断によって,こどもがどこに困難を感じているかを明らかにすることが必要である。そして,その困難が明らかになったら,具体的なものを使って,その困難を克服していくために必要な基礎的な概念をしっかり作り上げることがたいせつである。この場合の指導を,一つの例について説明しよう。
位取りの原理,言い換えると,数と記数法との関係について,具体的なものを使って指導するくふうを述べてみよう。
(ⅰ) おはじきを,「さんじゅうろく」取らせる。
(ⅱ) 次に,赤のおはじきは1個で10,青のおはじきは1個で1を表わすとして,上にとったおはじきを簡単に表わす方法をくふうさせる。
下の図で,○は赤,●は青を表わしている。
おはじきを使って,やさしく数を作ることができるように練習する。
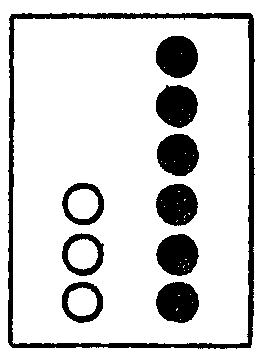
(ⅲ) さらに,上のように並べた10の玉,1の玉の個数を次のように書き,それで,はじめに取った「さんじゅうろく」を書き表わす。
いろいろな数について,このような指導をしているうちに,書かれた数字は,書かれた位置によって,その表わしている大きさに違いのあることが明らかにされていくのである。このようにして位取りの原理ができ上っていくのである。
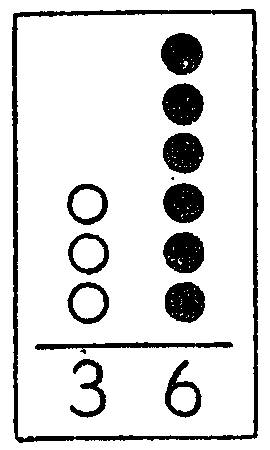
(ⅳ) 今度は,35,82,76,……等と言うように,数を数字で示しておき,おはじきを使って並べさせる。
こどもは感覚をとおして,手の筋肉をとおして,数の大きさや位取りの原理をしっかり作り上げていくわけである。とにかく,できなくて困っているこどもは,抽象的に話してもわからないのが普通である。その場合に,できるだけ具体的なものを使って,事がらの本質を明りょうにするように指導していけば,おくれているこどもや,できないでいるこどもも,理解をもって学習していくものである。この場合に,事がらの本質を見失うような具体的なものの使い方は,ますます混乱を大きくするものであることに注意したいのである。
(d) 先に指導したものが身につくまでは,新しい事がらについての指導に移らない。
こどもは,とかく先を急ぎたがるものである。ふじゅうぶんなままに,次々と新しいことに進んでいきたがるので,そのままに放任しておいたとすると,初めのうちは,どうにか進んでいけるものであるが,そのうちにどうにも進むことができなくなるものである。このようなことでは,できなくなったときにその原因をつきとめて指導しようとしても,あやふやなところが多いために,何を指導したらよいかを見さだめることに,非常に困難を感じるものである。とにかく,ここまではしっかり学習ができていると,はっきりいえるように,着実にこどもが学習していくように,指導することが必要である。
(e) 個別指導に適した教材教具を使う。
診断的指導では,こどもの能力に応じて学習を進めていくことができるように,指導しようとしているのである。したがって,こどもの学習に用いる教材教具も,こどもがめいめいの学習の速さに応じて,学習していくことができるようなものを,選ぶ必要がある。たとえば,位取りの原理についての指導をするのに,黒板の上だけで指導していくようなことでは,じゅうぶんであるとはいえない。こどものひとりびとりが,自分で手に持ったり,動かしたりして,自由に学習していくことができるようにしなくてはならない。
(f) 指導のはじめに当って,100%に正しくできるまで指導を続ける。
これと同じようなことは先にも述べたことである。指導を進めていくときに,単に診断的指導だけではないが,指導の初めが最もたいせつである。この時期に,完全に正しくできるまで,気長に指導しないで先に進んでいくと,もしも,誤ったくせができたとすると,これをなをすのに,たいへんな努力を必要とするものである。いわば,わるいくせが固定していけばいくほど,この固定した悪いくせが取りにくくなるものである。たとえば,九々の指導をするときに,指導の初めに,どの九々も正しくできるまでに指導することを忘れているために,小学校6年生になっても,正しく九々のできないこどものいることがある。
このような理由から,はじめの指導をおろそかにしないようにすることがたいせつである。しかも,診断的指導では,こどもの進度がまちまちになり,ややもすると,このことについての考慮が忘れられがちになるのである。
(g) こどもの当面している実際の問題やその他の学習活動において,学習したことを適用してみることができるようにする。
診断的指導は,前にも述べたように,数学的目標の主要部分を占めている技能を伸ばすために考えられたものである。したがって,この方法で指導されるものは,計算問題や事実問題で,いわば書かれた問題である。算数の指導のねらいは,書かれた問題を解決することができるようになるだけで,じゅうぶんであるとはいえない。こどもの当面している実際の問題や,算数以外の学習における学習活動で,算数を使いこなすことができるようにしなくてはならない。
このような機会があるように,教師のほうで計画をたてておくと,こどもは自分の学習したことの役だつこともわかり,また,成功の喜びを味わうこともできる。これが動機となって,さらに自学自習していこうとする意欲を起させることもできるのである。また,学習が単調でなく,変化をもつようになるものである。
(h) 診断テストを使って,どのこどもが,どんな点についての指導を必要としているかを明確にとらえる。
こどもが計算を誤ったり,測定が不正確な場合など,困難に当面しているときには,教師はこどもがそれを克服して,正しく計算し,正確な測定ができるように,指導の対策をたてなければならない。じょうずな指導は,こどもの混乱や困難をまねいている原因を見きわめたときに,教師の口から直接その原因を伝えて,こどもを恥ずかしがらせるようなことをしないで,できるだけ,こども自身が困難の原因を見つけるように導き,さらに,こどもみずからの意欲と力で,その原因を除去するように援助することである。
このように指導の対策を立てるためには,こどもの困難が,正しく仕事をする習慣がないために起るのか,また,計算や測定等の過程についての理解がふじゅうぶんなためなのか,あるいは,基礎的な事実についての知識が欠けているために起っているのかなどと,その原因を,診断テストを使って,明確にとらえることが必要である。
(i) 診断テストによって,困難の原因が明らかにされたら,それに必要な指導の準備をする。
前の項で述べたように,きちんきちんと計算する習慣がないために,誤算をする場合がある。このこどもに対しては,きちんきちんと正しい手続のもとに学習を進めていくように気づかせて,自分の仕事のしかたを修正するように指導の準備をしなければならない。
また,計算の基礎になる事項についての理解が不足しているために,誤算を生じていることが明らかになったら,その理解についての指導の準備をすることも必要である。
この準備をするときに注意してほしいことは,学習指導法の第1部第3節で詳しく述べているように,こどもに直接している具体的なものを使って,感覚をとおして理解していくように,指導することが必要である。そして,こどものすでに持っている経験と,新しい経験とを比較して,じゅうぶんにその関係を明らかにして自分のものとし,取り入れるようにすることも忘れてはならないことである。理解をもって学習していくようにするためには,第4節で述べたことを参照してもらいたい。
また,基礎的な事実についての知識が欠けている場合の指導の準備であるが,こどもの身近な生活に起ることで,同じような事例をできるだけ多く集めることがたいせつである。
(j) 使わないでいると,一度得られた技能も失われていくかもしれない。このようなことが起らないようにするためには,すでに指導したものがくり返し練習できるように,適当な機会を設けるように心がける。
第1節に「よせ算」についての段階を示したが,各段階ごとに問題カードを印刷して,教室の一定の場所に整とんしておく。こどもは,必要なカードを取ってきて学習するのであるが,カードに答を書き入れないようにすると何度もくり返して使うことができる。少しくふうしておけば,これを来年のこどもも使用することができる。
このように問題カードを,段階順に番号をつけて整とんしておけば,すでに学習したものでも,必要に応じて利用することができる。教師は,一度得られた技能も使わないでいると失われるかもしれないので,時おり,こどもにあとをふりかえらせて,前のものをもう一度練習させるように,意識して計画を作ることが必要である。
また,かけ算になると,ある長い期間,かけ算だけに熱中する傾向がある。この場合には,教室の背面に整とんしてある加法や減法のカードから,適当な段階のカードを指示して,短時間ずつ練習するような機会を作ることも望ましいことである。
要するに,準備したカードは整とんして保管しておき,必要に応じて使用することができるようにしておくことがたいせつである。
以上は,診断的指導について述べたのである。この指導は主として,数学的な目標の達成をねらっていくときに用いられるもので,これだけで,算数についての指導のねらいの全部を達成することができないのである。この点については,じゅうぶんに留意してもらいたい。とにかく,こども自身が自己の学習の目標を明確につかんで,しかも,あやまりなく正しくその目標に到達することができるようにすることは,容易なことではない。しかし,技能を身につけたり,また忘れないで必要に応じて使えるようにするために,練習の機会を与えるには,診断的指導はすぐれた一つの指導の方法である。
2.反復練習の実際指導
今までに,反復練習の実際の指導に関係したことは,いろいろなところで述べてきた。ここでは,重復もかえりみず,これをとりまとめて述べることにする。この指導法を,特に二つに分けて述べることにする。この指導法を,特に二つに分けて述べることにする。前半においては,一般に,反復練習をどのように指導したらよいかについて述べることにする。後半においては,反復練習で,こどもが正しくできるようにすることは重要てあると考えられるので,特に,こどもが正しくできるようにするために必要な指導の着眼点をあげることにした。ここで述べたことと,第1部の第7節で述べたこととを考えあわせて,反復練習の効果がいっそうあがるように指導したいものである。ややもすると,反復練習はただくり返し練習する機会を設けさえすればよいといった程度に考えて指導されやすいが,それでは,その学習に対する効果をじゅうぶんにあげることができない。
反復練習の指導にあたって,一般にどんなことを考えておいたらよいか
ここでは,さきに述べたように,まず,一般的な指導上の留意点を,とりまとめて述べることにする。
(1) 反復練習に先だって理解を伸ばしておくことがたいせである
例を2年生の「おみせごっこ」の学習をして,ひき算の指導をする場合にとって,ここで述べようとしていることの意味を明らかにしてみよう。
どの店の品物が安いかと言うことを調べようとすると,店の品物のねだんを比べてみることが必要になる。そのときに,いくら安いか,いくら高いかを調べるのに,ひき算をすればよいことがわかってくる。
一つの店で買物をするときでも,品物によってねだんが違うところから,いくらの違いがあるかを調べるのに,ひき算をすればよいことがわかってくる。また,おかねを払っておつりをもらうときにも,ひき算をすればよいことがわかる。
このようにして,すべて二つの数の違いを見ようとするときには,ひき算を適用することができることを指導する。こどもは,このようにして,どのようなときに,ひき算を使えばよいかを理解するのである,しかも,おかねやおはじきを使って,位取りの原理との関係を明らかにしながら,ひき算の手続について理解するのである。このように,ひき算の意味や,ひき算の手続についての理解ができたところで,ひき算についての反復練習の指導にはいるわけである。ところが従来,こどもの理解に対しての指導を軽く見て,一,二の例だけで,すぐに反復練習に移り,反復練習の日数を多くしさえすれば,計算ができるようになるものと考える向きも見られた。このように理解できていないことを,どのようにくり返し練習してみても,すじみちをたてて,論理的にものごとを考えていく力は伸びないので,機械的に記憶するにとどまってしまうのである。しかも,どうしてそのように計算してよいかとか,どんな場合にその計算を使ったらよいかとかがわからないのでは,日常生活に算数を生かすようなはたらきが養われないことは明らかである。このような意味から,反復練習に先だって,まず,じゅうぶんに必要な理解を伸ばしておくことが必要となるわけである。
(2) こどもが学習する必要を感ずるものを取リあげ,これをきっかけとして反復練習にとりかかるようにさせる
4年生で,珠算による加減についての反復練習をする場合について述べてみよう。一応計算のしかたについての理解ができたあとで,学級費や給食費,遠足の費用についての計算をしてみる。すると,まちがいが多くて,容易に正しい答が出てこない。そこで,どんな計算の場合にまちがいが多いかを調べてみるのである。すると,繰上がりの回数が多い場合であるとか,ひき算が途中にはいってくる場合であることが明らかにされてくる。ここで,こどもは,どのような種類の計算がまちがいやすいかを,はっきり意識するのである。このような機会をとらえて,反復練習するように指導すれば,こどもも練習をする理由と必要とがはっきりわかるから,効果的な反復練習を行うことができるわけである。
(3) 反復練習は,個々のこどもの能力に応じてできるようにする
できぐあいは,こどもによっていろいろ違いがあるものである。あるこどもは程度の高いものでも速くできるし,あるこどもは学年が同じであっても,程度の低いものに,ずっと多くの時間をかけなければならないであろう。これは,われわれの指導で,いつも,見られるとおりである。それにもかかわらず,いっせいに同じ計算などを同じ時に練習させたとする。これは遅れているこどもにとっては,とてもむずかしくてできないものであろう。また,進んだこどもにとっては,とてもやさしくて,足踏みをさせるものであろう。このようなことの起らないようにするためには,めいめいのこどもが,自分の程度にあった練習ができるようにしなければならないわけである。
たとえば,かけ算九々を練習するのに,いつもいっせいに声をはりあげて,「二一が2」「二二が4」「二三が6」…と「九々81」まで練習するような指導がある。
これに対して,こどもがめいめいに,表には問題,裏には正しい答を記入したカード(表……(□2×1裏□2表□8×6裏…□48)を2のだんから9のだんまで作ったものを持っている。そして□2×1のカードの表を見て,「二一が2」と唱え,となえた結果が正しかったかどうかは裏をみて,確かめながら練習する。もし□7×6を見て「七六48」と唱え,カードの裏を見ると□42となっていて,誤っていることがわかったときには,そのカードを別にしておき,あとでその九々だけは,特別に回数を重ねて練習するように指導するのである。また,カードによって練習させ,自分の誤ったものには,カードの表に印をつけさせる。印のついているカードについてだけは,特別に多く練習させるように指導する。とにかく,あとにあげた二つの指導では,こどもが能率をあげて学習をすることができるであろう。しかも,このように指導すると,こどもは,めいめいに自分のできにくいものをより多く練習することができ,こどもの能力に応じて反復練習をすることができるのである。
(4) 簡単な計算や測定などでも,多くの時間をかけるようにする
たとえば,2年生の二位数に一位数を寄せて繰上がる計算の練習について考えてみよう。この種類の計算は,よせ算の中で最も簡単なものではあるが,けた数の多い数についてのよせ算,かけ算などのもとになるものである。とにかく,繰上がりのある計算の基礎となるものである。このような意味から見ると,この計算は,このあとの計算ができるようになるかどうかに,大きな関係をもっているものであると言える。ところが,おとなのわれわれから見ると,この計算は,きわめてやさしいもののようにみえるかもしれない。これは,あとの計算までのできる人にとってのことである。これから学習していくこどもは,二位数に一位数をよせる計算で,繰上がりのある計算の原理について学習する。このあとで,二位数に二位数を加える計算で,繰上がりが二回ある場合の初歩の学習にまで及ぶのである。このようにして,学習を進めていくこどもにとっては,徐々に困難を克服していくのであるから,われわれから見てやさしいものでも,こどもにとって,決してやさしいものではない。これに対する錯覚からか,低学年の指導をややもすると軽視して,基礎的な事がらについての指導を怠ることがある。これが,そもそも4年生ぐらいから,できないこどもができてくる原因となっているのである。いわば,一段ごとに学習することがあるから,こどもにとっては,いつも同じように困難があるとも言える。このような理由からやさしく見えることでも,こどもにもやさしいと考えてならないのである。
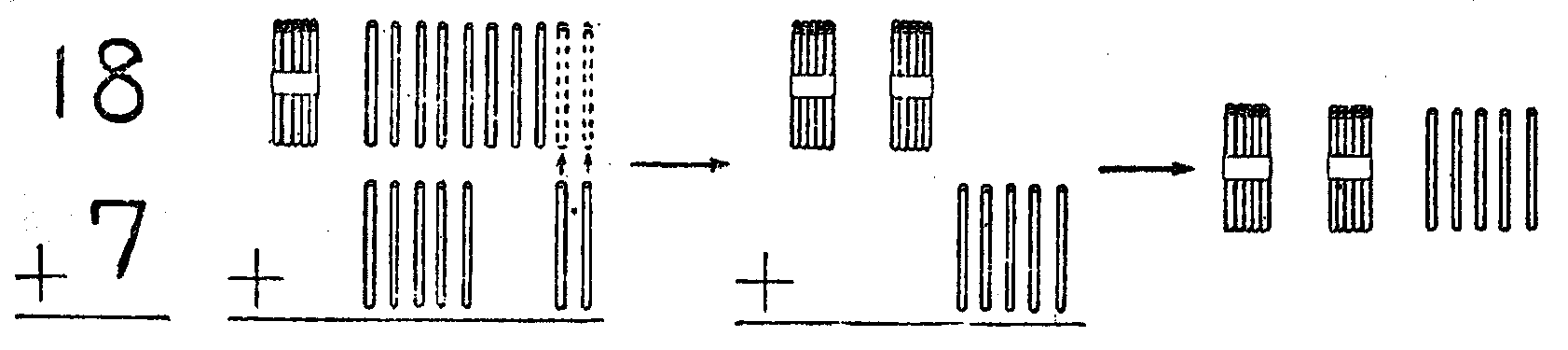
たとえば,18+7のような計算でも,これについての理解が一応できたからといって,そのあとでは,いつも抽象数だけで練習するので,じゅうぶんではない。教室に割ばしなどを用意しておいて,これを用いて,具体的な行為と式とを結びつけ,くり返し繰上がりのある計算の原理を指導することを忘れてはならない。しかも,これができたところで,形式的な反復練習も必要となるであろう。このようにして遅れているこどもも,だんだんにできるようになるであろう。とにかく,おとなのわれわれから見てやさしいものは,一般に原理的なものであり,最も基礎的であり,最も重要なものである。しかも,こどもには決してやさしいものではない。このような意味からも,簡単な計算や測定であっても,この反復練習にじゅうぶんな時間をかけて,どのこどもにもできるようにしておくことが必要である。おとなから見てやさしいからといって,これにじゅうぶんな時間をかけないようなことでは,このあとに続く指導に,支障になることを注意したいのである。
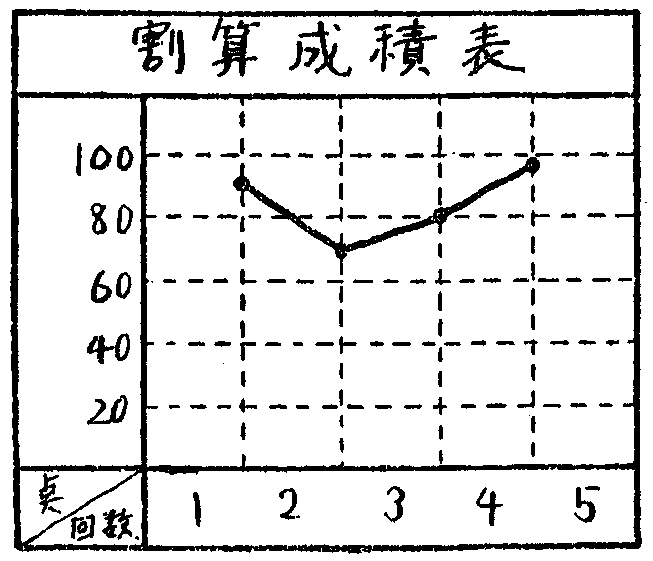
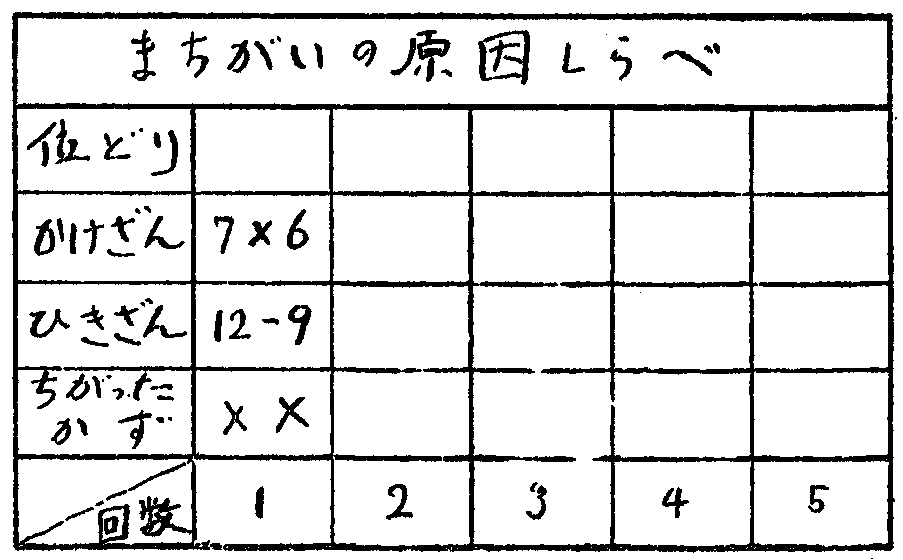
(5) こどもが自分の進歩を見守ることができるように,めいめいが,成績を記録しておけるような方法をくふうしておく
反復練習に当って,練習の効果が目に見えるようにすることは,こどもたちに練習の意義を知らせる上に有効であり,また,さらに自分から練習しようとする意欲を起させたり,練習の箇所を知る上に,たいへん重要なことである。たとえば,わり算の練習を一回に五題ずつ練習することとし,この結果のできぐあいを記録して,だんだんに速くできるようになってくるかどうか,正答数が多くなってくるかどうかを観察する。この場合に,めいめいが自分の進歩を見ていけばよいのであって,他の人のと比べさせる必要がないことに注意したいのである。記録としては単に正答数だけでなしに,どこでまちがえたか,誤りの原因を記録させるようにするのもよい。いつもひき算で誤るとか,かけ算九々で誤るといったことが,はっきりしてくれば,自分の成績をあげるためには,どんなことに努力したらよいかが明らかにされてくるであろう。
このようにして,自分の成績の変化が見られるようにすることは,自主的に反復練習させる上にたいへん有効な方法である。記録の方法は,低学年では○や×を用いてわかりやすく記入させ,高学年では,点数を用いたり,棒グラフや,折れ線グラフを使って,なるだけ前後の比較がしやすいように書いておくがよい。
(6) こどもが,こちらで考えている望ましい程度にできるようになるまで,反復練習する
かけ算九々の反復練習にあっては,九々が自由に誤りなく言えるようになることが望ましいわけである。しかし,これにもいろいろな段階がある。順序どおりに2×1,2×2,2×3,……と9×9までいえるものもあろう。順序をとりまぜて,9×3でも,7×6でも,どのような順序に出されても正しくいえるものもあろう。さらに,積48を見て,二つの因数6×8と8×6というように答えられるものなどもある。3年生のかけ算九々の指導としては,だれもが,順序不同でも正しくいえるまでに練習することが必要である。また,速さはそれほど要求しないにしても,途用でつかえないで,因数と積とをすらすらと言える程度にまで練習することが必要である。ところが,ややもすると九々のように基礎的なものを,簡単であるように考えて,反復練習することをないがしろにすることがある。これでは,あとの計算にひどく困難を感じ,できなくなっていくのは当然のことである。
(7) 反復練習をするに先だって,計算や測定などの手続が正しくできるようになり,それが習慣にまでなっていることを確かめる
技能の学習には,まず理解を持たせて,その手続を知り,それが実際問題に正しく適用できるように,いろいろな事実に対して,実際に使ってみて,それから反復練習に移るがよい。従来,算法がじゅうぶんに理解されないままに,算法を実際問題に適用できないままに,その計算を反復練習をさせることがあった。そのために誤った手続や能率のあがらない手順であっても,これを,正しくする機会が失われてしまうことがあった。このような意味から,正しい手続が習慣にまでなっていることを確かめてみる必要がある。それには,反復練習の前にじゅうぶんな時間をとり,時間の不足のためにできない原因をつくらないように,考慮しなければならない。かけ算九々であったら,一応正しく言えるまでになったかどうかを確かめるのである。物さしの使い方や,はかりの使い方であったら,いろいろなものを実際に測定させてみるのである。このように時間をかけさえすれば,誤りなく目もりを読むことができることを確かめることができる。このあとで反復練習にはいるならば,こどもが誤って理解しているままに,計算や測定の手続が固定してしまうことがないから,反復練習によって,正しい技能を身につけることができるのである。
反復練習で,こどもが正しく仕事ができるようにするためには,特に,どんなことを考えておいたらよいか
ここでは,さきに,正しい計算や測定の習慣ができるようにするための留意点を,とりまとめて述べることにする。
(1) 正しい形式を,こどもが理解していることを確かめる
反復練習が,正しく行われるようにするために,注意してみておかねばならないことの一つは,こどもが正しい形式を理解したかどうかということである。先生が注意しないでいたために,答だけは正しくできていても,よくない方法をおぼえたままで,それが固定してしまった例がある。それは左のようによせ算に際して,暗算式に上位から決めていく方法をとり,5+8では13として,すぐ下に13をかきしるしてしまう。そのあとで下の位の7+9を計算して16を求め,そこで十位の3をゴム消しで消して,4と書きかえるというような手続をとっていたのである。
あるいは,導入の際に,こどもたちが考え出した不完全な形式を,そのままいつまでも続けていくような場合もあるから,そうしたよくない形式が固定していないかどうかを確かめておくことがたいせつである。
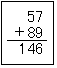
(2) 正しい仕事の習慣ができるまで,その練習を教師はしっかり見守っていなければならない。これがないと誤った習慣が固定するからである
1年生のこどもは,数字の書き順や書き方を誤っているものがある。練習以前にこれを発見してきょう正することは必要であるが,一度訂正しておいたからといって,正しくできるようになったと見ることは,時々誤りである場合がある。反復練習に当って注意してみると,再び逆もどりしている場合が少なくない。そこで,教師の注意しなければならないことは,いつどこで行っても,正しく使っていく習慣ができあがるまでは,いつまでも注意することである。こうした教師の注意が,どこまで続くかによって,悪い習慣の克服ができるかどうかが決まってくるとみることができる。
(3) 準備のための反復練習をしていても,いつもねらっている反復練習と結びつけるようにする
例を異分母の加減計算を指導する場合にとって,これを説明しよう。2/3+1/4ができるためには,分母が同じであることが必要になってくる。そこで共通分母を見いだすために,3と4の公倍数を求めなければならない。そこでできるだけ早く,しかもできるだけ簡単な計算で求められるようにするために,最小公倍数の求め方を学習することになろう。さて,その方法が理解されたところで,反復練習をする必要が起ってくる。このようにして,すっかり最小公倍数の反復練習ができたところで,通分の指導が再び取り上げられるとする。ところが,通分やよせ算の練習は,ここでねらっていることの反復練習であり,公倍数,最小公倍数についての反復練習は,準備のためのものであるとみることができる。このような場合に,準備のための公倍数に関する練習が長すぎたために,それが何のための反復練習であるか,こどもにわからなくなってしまうことがある。こうしたことがないようにするためには,最小公倍数の学習がすんでから通分にもどるというのでなしに,(2,4),(3,6)等のように,一方を何倍かすれば,すぐに,他方が最小公倍数である場合の学習をしたら,1/2+1/4,2/3+1/6等の加法を練習し,(3,2),(4,7)等のように二数をかけて公倍数が求められる場合を学習したら1/2+1/3,1/4+3/7のような加法を扱うと言うようにして,いつも最後の段階の練習と結びつけて扱っていくことがたいせつなことと言えよう。それなしには,こどもは反復練習したことを計算に結びつけることができないため,正しく計算することができないことがある。
(4) ある一つの技能を導入するには,その前に指導した技能を仕上げておかなければならない
左のようなかけ算の指導をし,その練習を行ったあとで,左のような計算をさせてみると,5に4を寄せ,また3にも4を寄せて79とするこどもの見られることがある。これは,35×4の方法を練習した結果,乗数を被乗数の各位の数字にかけることを知って,よせ算の際にも,被加数の各位の数字に加数を加えてしまったのである。こうしたことが起るのは,かけ算の前によせ算の反復練習がじゅうぶんされないうちに,かけ算を練習したために誤ってしまったのである。このようなことのないようにするには、二つの方法を混同しないように,前の技能についてじゅうぶんに練習することがたいせつである。
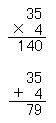
また,かけ算が正しくできるためには,4×5,4×3のかけ算九々,つまり4の段の九々か誤りなくできることがたいせつである。もとになるかけ算九々の練習をしないで.二位数のかけ算をいくらやっても,決して効果の上がるものではない。
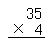
(5) 習慣形成の初期においてはゆっくり進めていく
二位数と二位数のよせ算で繰上がるものは,2年生の教材のうちで,最もむずかしい教材の一つであるというところから,練習を多くしなければならないことは認められている。初めから速度を要求しすぎると,けたをそろえることや数字を正しく書くといった習慣が養われないために数字をよみ違えたり,(たとえば6を8と書いて,8ととり違える)よせるけたを違ったりして,かえって誤りを多くすることがある。反復練習の初期には,できるだけ時間的には制限を加えず,正しい形式で数字や記号をできるだけ正確に書く習慣をつくることに努め,そうしたことが正しくできるようになったところで,速度を早めていくようにするのがよい。
(6) 初めは重要なねらいだけが正しくできるようにする。そうしてその他のねらいを徐々に加味していく
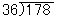 のような計算の練習をはじめるに当っては,商に,誤りのない数が正しい位置に立てられるようにすることがたいせつであって,計算の初めから,最も早く商を見いだすにはどんな九々から考えるのがよいかとか,文字をきれいにといったことをいろいろあげると,こどもは最も大事なねらいが何であるかがわからなくなってしまうおそれがある。初めは正しい答が正しい手順で出せればよいということにして,少しは遠まはりな方法であってもこれを許容するのである。正しくできるようになってきた時を見はからって,徐々により早く商を立てるには,九々は6あたりから考えてみたほうがよいとか,数字は正しくといったことに注意を及ぼしていくのがよい。これは前項(5)に比べて矛盾しているようにも考えられるが,(5)に先だって指導されるべきもので,指導の重点を一つずつはっきり定めておき,学習させたらよいことを注意したものである。
のような計算の練習をはじめるに当っては,商に,誤りのない数が正しい位置に立てられるようにすることがたいせつであって,計算の初めから,最も早く商を見いだすにはどんな九々から考えるのがよいかとか,文字をきれいにといったことをいろいろあげると,こどもは最も大事なねらいが何であるかがわからなくなってしまうおそれがある。初めは正しい答が正しい手順で出せればよいということにして,少しは遠まはりな方法であってもこれを許容するのである。正しくできるようになってきた時を見はからって,徐々により早く商を立てるには,九々は6あたりから考えてみたほうがよいとか,数字は正しくといったことに注意を及ぼしていくのがよい。これは前項(5)に比べて矛盾しているようにも考えられるが,(5)に先だって指導されるべきもので,指導の重点を一つずつはっきり定めておき,学習させたらよいことを注意したものである。
(7) 個人差を診断することができるような反復練習のための教材・教具を用意する
かけ算の指導で,反復練習に先だって,かけ算九々,かけ算の方法,繰上がり,よせ算,位取り,数字等の項目を縦に,こどもの名を横に取った一覧表を用意しておいて,教師がこれにテストや,観察の結果を記入したり,あるいは,児童各自にそうした表を持たせておき,どこが原因で誤ったかを表に記入させ,特に誤った部分をより多く練習させるのである。また,かけ算九々,よせ算九々,ひき算九々などを練習するときに,カードを作り,練習している際に誤ったものには印をつけさせておいて,後で誤ったものだけについて練習をくり返し行うようにするのである。これは,速度を早めたり,むずかしい問題を克服する上に経済的な方法である。こうした結果,あるこどもは0とのこのよせ算を多く誤ったり、あるこどもは繰上がりの数を忘れることなどがわかり,そうした問題について,自分から練習するようになっていくものである。
(8) 初めは量が少なく,あとになるほど間隔が遠くなるようにする
三位数と二位数または三位数とのかけ算とか,四位数または五位数を二位数または三位数でわる計算といったもは,初めは毎日一,二題ずつさせることによって,その算法をはっきり理解させることに努め,次には三題ぐらい,次には五題ぐらいと数を増していくのがよい。また,練習する日の間隔も,初めは毎日であったものをある程度できるようになったら,二日置き,やがて五日置き,それから一月ごとに練習するというようにする。ある程度できるようになったところで,反応に要する時間があまり低下しないように注意すればよいわけである。つまり,問題の数を初めは少なくし,だんだんに増していき,練習の間隔を初めは短く,だんだんに長くするのがよい。
(9) すでにできている習慣は,それがめいりょうに悪くない限り,変える必要はない
たとえば数字を斜体で書くようになっていたり,珠算を一本指だけでしたりするような習慣は,それが誤りではないから,しいて,これを注意して,なおさせる必要はなく,そのまま継続させてよい。
ものさしの使い方にしても,目もりが手前になるようにはかったりしても,時と場合により,はかりよいこともあるから,必ずしも一つの方法に合致していないからといって,これを改めさせなければならないと考える必要はないのである。
(10) 困難の原因を見いだすために診断テストを使い,時々大きな声でいわせるように指導する
診断テストを用いて,こどもがどれだけのことは理解できて,どの点で困難を感じているかを見いだすことができる。また,算法や測定法などを口答で発表させ,その発表で誤って理解しているところを知ったり,または,発表ができなくなったことから,どこでつまずいているかを知って,困難の箇所や,誤りの箇所を知り,これを訂正するようにする。たとえば診断テストの結果,7時50分を8時50分と読むこどもの多いことがわかったとする。その原因は,時計は短針だけでは読みにくいところを,長針によって補うようにできていることの理解が,ふじゅうぶんであったことが原因であるとわかったら,特にこの点に重点をおいて指導していくのである。
(11) 診断が終ったら,ある特定のこどものもっている困難を克服するための反復練習をする
一般的な困難などは、前項のようにして全体の児童に指導するが,あるこどもは,6年生になって,「八六,48」と「六七,42」とを誤っているものがある。このような場合には,そのこどもだけに特に,カードを作って練習させるといったような方法で特別指導をする。ただ注意しなければならないのは,遅れているこどもを全体の前で恥をかかせるようなことはしないようにして,一人ずつ,あるいは,同様のこども数人を教師の近くに呼んで指導するような心がけがあってほしいものである。
3.技能の維持
| どのように指導したら,技能が必要に応じて使えるように身についているか。 |
近ごろの小学生や中学生の卒業生の中には,簡単な計算さえもできない者が多いといわれている。これらのこどもは,その計算の指導を受けなかったのではなく,卒業した後までも,学習した技能を忘れないで,必要に応じて使えるようになっていなかったからである。技能を一度学習しても,そのままに放っておいたのでは,一般に,その技能は忘れられていくものである。たとえば,4年生の時のやさしいかけ算でも,一度指導しただけで,6年生になるまで,その指導がなかったならば,6年生には決してやさしくできるものではない。
技能が身についていて,必要に応じて使えるようにするためには,どのようなことに留意したらよいかを考え,そのおもなものをとりあげてみよう。
(1) 数学における原理は数学全般にわたっているものであることが,いつもわかるように指導する
今までは低学年で指導したことが,高学年あるいは中学校までの学習の基礎となり指導内容が有機的なつながりをもって発展していくように指導されなかったといってよい。こどもの経験は,常に既往経験を核として,それに新しい経験が加わってより大きな核となり,さらにまた新しい経験が加わるというように拡張されていくものである。しかも,その発展していくときの原理となるものは,数学全般に通ずるものであって,決して技能は個々ばらばらなものではないのである。このような考慮がなかったら,一度指導された事がらは,二度と指導される機会がないので,忘れられていくのである。また,一度忘れても,原理が同じであると,やさしく思い出す手がかりがあるので,これを思い出すことができる。しかし,ささえている原理がなかったとしたら,思い出すための手がかりは失われているので,どうにもならないのである。これを,例について,具体的に説明してみよう。
百分率を指導する場合には,それを今まで学習してきたこととは全く別な新しいものとして指導しないのである。すでに学習してきた分数と結びつけて指導するのである。すなわち二つの量の割合を表わすのに,わり算をして,整数や小数で表わしたり,分数で表わしたりしてきたのである。分数で表わすとすると,分母をいろいろにとることができるので,割合を表わすのに,つごうのよいこともあるが,分数で割合を表わしたのでは,割合の大小を比べるのには手数のかかることがある。そこでこれを比べやすくするには,分母を定まった数にしておくのがよい。そこで,割合を整数や小数で表わしたときのことからみて,分母が立100,1000などを用いると,つごうのよいことがわかる。このように,今までに指導してきたものと結びつけながら,分母が100である分数の分子で割合を表わすことにして,分母が100であることを示すために%の記号を用いることを指導するのである。このように指導していけば,今までに指導した分数や小数あるいは整数についても指導する機会があり,こどもが今まで学習してきたことを思い出すことができ,技能は推持されていく。
もう一つの他の例をとりあけてみよう。よせ算は,加え合わせる数が整数であっても,小数であっても,また,諸等数や分数であっても「単位をそろえること」「各くらいの和が上位の単位でまとめられるまでになったら,上の単位に繰上げること」の二つの原理によってできるものである。このようなわけであるから,小数を指導する場合には,すでに学んだ整数と結びつけていく。諸等数たとえば時間の加法を指導する場合には,十進数との違いは,60が単位になることのほかは,整数や小数の加法と同じ原理でできることを指導していく。また,分数を指導する場合には,単位がその分数に応じて異なることのほかは,十進数や諸等数の場合と同じであることを指導していく。このように指導すれば,今までに学習したものをとりあけていくことができるので,指導する機会があるから,技能はいつも忘れないでいて,維持されていくものである。
このように新しいことがらでも,それが出てくるごとに今までに学習したことと結びつけ,今学習しようとするとこの位置づけを明らかにすれば,新しく理解したり,記憶したりする事がらも少なくてすみ,数学がどのように発達してきたかもこどもながらにわかるであろうし,学習した技能はおのずから身について,いつまでも忘れないでいて,必要に応じて使えるようになるであろう。
(2) 学年の初めに,こどもを調査して,それに応じて指導計画をたてる
こどもは一度学習したことがあるといっても,今それを忘れないで知っていると考えてはならない。そとで,教師は学年や学期の初めには,こどもが今までに学習した事がらについて,忘れているものはないか,また,現在どの程度知っているかについて調査するのである。もし,こどもが忘れていることがあったら,それをできるだけ多くの時間をとって,じゅうぶんに指導したり,練習させたりするのである。このようにして,新たに学習を始めるための基盤をつくるとともに,今まで学習した技能が確実に身につくように指導するのである。
また,一度学習したことが身についていくようにするためには,あらかじめ指導計画をたてるときに,再びそれを指導したり,練習したりすることができるような機会を考えておかなければならない。たとえば,除法の学習をするためには,そのもとになる,ひき算やかけ算九々ができなければならない。そこで除法の学習に困難のないように,それ以前に,ひき算やかけ算九々の学習が何回もくり返し練習することができるように計画しておくことが必要である。
このように,ひととおり学習したらそれでよいとするような平板的な指導でなく,一度学習したことでも,機会のあるごとにくり返し指導したり,練習させたりすれば,学習した技能はおのずから身についてくるであろう。
(3) 診断テストによって,基礎的な技能で弱いところを見いだし,それを補強するために,もう一度指導する
教師は新しい学習を展開するに先だって,その学習を進めるための基礎的な技能について診断テストを行い,もし,こどもに弱いところがあったら,これを補強するように,もう一度練習させたり指導したりすることが必要である。
たとえば,乗法を指導する前には,その基礎になるよせ算が,どの程度に身についているか,また除法の指導をする前には,その基礎になるひき算に弱いところがないかどうかというように,常に新しい学習に入る前にはそのもとになる基礎的な技能を調べて,必要があれば,もう一度くり返し指導したり練習させたりするように留意しなければならない。
また,さらに必要があれば,標準テストや教師のつくったテストをしたり,できれば前の担任教師や父兄と話合いをしたりして,もう一度指導したり.練習したりする必要があるかどうかを調べ,これに基いて,指導や練習をくり返し行うならば,おのずから技能が身についていくであろう。
(4) 基礎的な技能をもっと進んだ実際的な仕事や問題に応用するような機会を作っておく
同数累加から,かけ算を指導して,こどもがひととおりかけ算の意味や九々がわかったら,それでかけ算の指導が終ったものと考えてはならない。これを,機会あるごとに,実際的な仕事や問題にも応用させるようにしなければならない。たとえば,長さの測定を指導したら,それを長さの計算のところでも適用したり,重さや容積の測定を指導したら,そのあとで,関係のある仕事や問題に適用させてみるのである。また,実務について学習したときには,そこで,実務について再びかけ算を適用させるのである。
このように,いろいろに適用できる問題の場をとおし,しかも,機会あるごとにくり返し練習させる間に,技能はおのずからこどもの身についていくものである。
以上述べたことは,要するに,記憶したり理解したりする事がらが多いと,それをいつも忘れないでいるということは,一般に困難なことである。そこで,それぞれの技能を個々別々のものとして記憶させるのではなく,それらの技能を結びつけている原理を中心において指導していき,くり返し指導する機会のあるようにしておくこどが,技能を維持していく上に重要なことである。
また,一度学習した技能はくり返し指導したり練習したりできるように機会を設けておき,それが気楽に使えるようになるまで,絶えず練習ができるようにしておくことも,技能を維持していく上に重要なことである。
4.論理的思考を伸ばすこと
| どのように指導したら,こどもの論理的思考を伸ばすことができるか。 |
算数科の主要な目標は,学校の内外に起る問題を,その必要に応じて,数量関係を用いて解決することができるようにするところにある。
そのためには,その場に応じて問題をとらえる力と,とらえた問題を解決するために必要な計算や測定などの技術が身についておらなければならない。ところが実際の指導についてみると,そのような問題がとりあげられたといっても,それは,計算や測定の単位関係などを導入するためで,導入できたところで,これを反復練習させることだけに主眼がおかれているといった感じがないでもない。問題解決の能力を伸ばさなければならないといわれていながら,このような指導になりやすいのは,計算の導入や反復練習などは問題を解決する能力を伸ばすための指導よりもずっとやさしくできるからであろう。一般に問題を解決することは,むずかしいことのように考えられているけれども,おくれているこどもでも,ものによっては,さほど困難なものではないのである。算数のよくできないといわれるこどもの中にも「抽象的な数についての計算はよくできないが,おかねはうまく取り扱うことができる。」こどもがあるものである。おかねのように,扱うものそれ自身が具体的であり,いつも,こどもの日常生活に用いられているものであると,豊かになった経験をもとにして,その問題を処理することができるのである。しかし,どの問題もこのように勘で処理することができるものではない。また,できるとしても,精神的な労力が大きく,すぐに疲れたりして,あやまりやすくなるのである。算数は,このようなことのないようにしようとして考えられたものである。したがって,学習指導においては,前に述べたような,やさしい問題解決の経験を基礎とし,これをもっと広い範囲にある問題,もっと複雑な問題の解決に導くことが必要なのである。ここに,諭理的思考を伸ばすことが必要になるのである。
ここでは,諭理的思考を伸ばすには,どのように指導したらよいかについて,具体的に述べることにする。
(1) 事実問題の解決と論理的思考
一般に,事実問題を解快することは,こどもにとって困難なことであるとされている。「計算はよくできるが,事実問題は解けない。」といわれることは,この困難さを物語っているものである。ところが実際には,さほど困難なものではないのであって,指導をくふうしさえすれば,もっとできるようにすることができると考えられる。いわば,指導のしかたにくふうがないから,こどもに困難なものとされているのではないかとさえ考えられる。例を,書かれた事実問題にとり,困難にしている原因とみられるものについて述べてみよう。
(a) こどもは,問題についてあまりよく考えないで,さっと読んでわからないと,すぐに処理に必要な数や方法を教師に問こうとする。ところがこのような場合に,教師はややもすると,こどもの考え方を練ることをさしおいて,すぐに,どんな計算でできるかと聞いたり,また,計算の方法を教えてしまうことが多い。したがって,問題を解決する場合に,どんな考え方をしたらよいか,言い換えると,問題解決をするために,問題の場をどのように組織だてたらよいかについて,こどもはほとんど指導をうける機会がないままに終ってしまうのである。このように,問題の場を組織だてることについて指導することなしには,問題を解決する力を伸ばすことができないと考えられる。
(b) こどもは,問題を解決する方法を教師に聞かないまでも,いいかげんに見当をつけて,何回も答を出してみることがある。その中で,これが正しい答らしいと思われるものを答とするようなことをすることもある。すなわち,問題をよく読んで,その問題の場を読みとり,それができたところで,これはよせ算でできるとか,ひき算でできるとかいうように考えないで,計算を深く考えて選ばないで,すぐに答を出してしまうのである。このような考え方をしていたのでは,事実問題の解決をいくら指導しても,問題を解決する能力を伸ばすことができない。これはまちがいないと自信のある結果を,いつも求めることができるようにするためには,問題を分析して,論理的に思考を進めることができるようにしなければならない。ここに,論理的思考が問題解決に重要であるといわれる理由がある。
(c) 論理的な思考力を伸ばすために重要なことは,問題を読んで,その問題の場を理解することである。その場が明らかにされないでいたのでは,その問題を解決するための目的に応じた計算を,用いることができないからである。したがって,書かれた問題の解決に対する指導にあたっては,まず,問題の場を読みとることができるようにすることがたいせつである。ところが問題には,その場の構造の簡単なものもあれば,複雑なものもある。おかねをもらうとか,買物をするとかのように,直接経験が土台になっている問題や,貿易とか人口のように生活には関係があるが,どちらかと言えば間接的と考えられるような問題もある。そこで,こどもに問題の場を理解させる能力を伸ばすためには,まず,簡単な問題,直接的な問題を読みとることができるようにし,しだいに,複雑な問題,間接的な問題の場を理解することができるようにすることがたいせつである。しかし,どちらにしても,論理的な思考力を伸ばすためには,こどもが読んで,ある程度抵抗を感ずるような問題がよいであろう。このような問題でないと,前にも述べたように,こどもが論理の裏づけのない勘で処理してしまうことがあるから,論理的な思考力をじゅうぶん伸ばしていくことができないのである。
(d) 今まで論理的な思考力は,問題の場を読みとることと深い関係があることを述べてきた。ここで問題を読みとるとは,どんなことをさしているかについて述べることにする。
(ⅰ) まず,これは,なにについての問題であるかに対して,答えることができることである。つまり問題の場全体の概観ができるということである。
(ⅱ) どんな事実が与えられているかに対して答えられることである。
(ⅲ) この問題は,なにをきいているかに対して答えられることである。
(2) 論理的な思考力を伸ばすための指導計画
問題の場を読みとるということは,今述べた三つの事がらがわかることである。
さて,問題を読んで,上の三つの発問に答えることができるようにするには,どのように指導したらよいかが重要な問題である。そこで,ここでは,書かれた問題の中でも,解決する場合に,条件が欠けているために困難になっているような問題は一応さけ,条件が完全に整って書いてある,次のような問題を例として取り上げ,論理的な思考力を伸ばすための指導のしかたについて述べてみることにする。
例① 図書室の本の貸出しの様子を調べてみると,4月には,296人のこどもが借りました。5月には,571人のこどもが借りました。5月には4月よりも何人多く借りたでしょう。
例② 花子さんは,95円の木を一さつ買いました。また,ふみ子さんは85円の本を一さつ買いました。この本のねだんはいくら違うでしょう。
例③ 理科班のものは,土曜日にこん虫や植物をとりに出かけました。学校を午前7時半に出て,10時間たってから帰りました。帰ったのはいつでしょう。
(a) 「これは,なにについての問題であるか。」をわからせるための指導について述べてみよう。
上の問題をこどもたちに提出すると,こどもたちはまず読むであろう。こどもが読み終ったところで,「これらの問題は,それぞれ,なにについての問題ですか。」と発問してみる。するとこどもは,きまって,それぞれの問題に書いてあることを,そのままといってよいかたちでくり返すであろう。たとえば,「図書館から,4月には296人,5月には571人のこどもが本を借りた問題である。」とか,「花子さんは95円の本を買い,ふみ子さんは85円の本を買った問題である。」とか答えるであろう。このような答は問題の場を理解した答であるとは言えない。ただ,問題に書いてあることを,そのままに述べただけである。そこで,教師は,前に述べた問に対して,どんなことをそれぞれの問題について考えたらよいかを,こどもの話合いによって研究させたり,また,教師が助言を与えたりして,それぞれの問題の場を全体としてつかみ,それについて答えられるようにすることがたいせつであることを明らかにする。
この問題の場を全体としてつかませるためには,実際に図書を借りることについて実演させてみることも結構であろうし,買物について劇化してみることも,また結構であろう。場合によっては,教師が問題の場を明らかにするために実演してみることも必要であろう。このようにして,それらのものの主題を何としたらよいかについて考えさせていくのである。
このようにして,こどもが問題の場を全体としてつかむことができると,こどもの答は,次のようにわかるであろう。
たとえば,①……「図書を借り出しているこどもについての問題である。」②……「花子さんとふみ子さんが買った本のねだんについての問題である。」③……「こん虫や植物さいしゅうに出かけた理科班についての問題である。」
また,このように答えられるようにしようとして,問題の場を解釈させるときには,数についての直接的な計算は一応考えないようにし,問題を一つの物語りとみなして,その筋をつかませるようにすることが重要であろう。
このように考えてくると,この学習活動は,読書における重要な一つの指導であると言える。すなわち,本を読んで,その筋道をしっかりとつかみ「ここには,こんなことが書いてある。」と,その大意をつかむことができるようにすることは,読書の指導では,きわめて重要なことであるからである。
算数においてこどもが,問題を解決する力が不足しているといわれる原因の一つは,このように問題の場を全体としてつかむ能力を,伸ばすことをしないでいるところにあると考えられる。
さて,このように指導を進めていくと,単に算数だけにとどまらないで,いろいろな本を読んだときにも,その大意をうまくまとめることができるようになるであろう。それによって,普通の本を読む力を伸ばしていくこともできると考えられる。また,級の者やその他の人が話をしたり,話合いをしているような場合でも,それを聞いていて,話の内容をうまくまとめることができるようになるであろう。さらに自分の話し方についても,その発問や答の質の可否がよくわかるようになると考えられる。
このような意味から「これは,なにについての問題であるか。」に対して,正しい答ができるようになることが,きわめて重要なものであると言える。
ここに,このような能力を伸ばすための実際指導にあたって,注意したらよいと考えられることについて述べておく。
前に述べたような指導をとおして,はじめは口頭で答えさせる場合が多いであろう。これは必要があれば,教師の援助によって,考え直して,すぐに言い直すことができるからである。しかし,いつもこのような方法をとっていると,こどもはあきてくるであろう。そこで,答をノートに書かせてみることも,たいせつである。答をノートに書かせてみるという方法は,単に,方法に変化を与えるというだけで取り上げるのではなく,必要なことばを選んで文章にまとめる力をつけることができるとともに,教師の側から言えば,こどもの,問題の場を全体としてまとめる能力を容易に評価することができるからである。
(b) 次に,「どんな事実が与えられているか。」をわからせるための指導について述べてみよう。
場の全体をつかむことができたら,どんな事実が与えられているかを,明らかにすることが必要である。
教師は,こどもに,どんな事実がわかっているかをたずねて,必要な事実を文章の中から抜き出させる。すなわち
例①……4月に本を借りたこどもは296人で,5月に借りたこどもは,571人であった。
例②……花子さんが買った本は95円で,ふみ子さんが買った本は85円であった。
例③……理科班は午前7時半に出かけて,10時間たってから,帰ってきた。
このようにすると,あとで演算するときにどんな数を使うかがよくわかり,また,その関係も簡単につかむことができるようになる。
(c) 「この問題は何をきいているか。」をわからせるための指導について,述べてみよう。
第2の段階で,与えられている事実がわかったので,その事実について,どんな関係があるかをつかむように指導していくのである。
例①……「5月に借りたこどもの人数は,4月より何人多かったかをきいている。」
例②……「花子さんとふみ子さんの,本のねだんのちがいをきいている。」
例③……「理科班のものが,帰ってきた時刻をきいている。」
ここまでくると,あとはその数量関係を処理するのに,どんな計算を用いたらよいかを考えて,それに応ずる演算を決定すればよいわけである。
ここまでが,問題を解決するための重要な段階である。このように問題の場をまとめたり,また,分析したりして問題の場を組織だてていくことができるようにすることが,こどもたちの問題を解決する能力を伸ばすことである。
この過程をいつも考えて,問題を解決することによって,こどもの論理的な思考力は伸びていく。
(d) 上の三つの段階にわたる指導の一般的な方法について考えてみよう。
まず,考えられることは,各段階ごとに練習することである。すなわち,いろいろな事実問題を用意し,それについて第1段階としての「これは,何についての問題であるか。」を中心に,問題の場の全体をつかむ練習をする。
また,第2段階,あるいは第3段階についても,このようにして,練習をするのである。それができるようになったら,そのあとで,問題が与えられたら,それについて,第1段階,第2段階,第3段階の順序に従って,問題の場を全体としてまとめたり,また,分析したりする練習をさせるがよい。
たとえば,例①について,次のように順序正しく考えていくように指導するのである。
○図書を借り出したこどもについての問題である。 (第1段階)
○わかっているのは,4月に296人,5月に571人である。 (第2段階)
○きいているのは,5月は4月より何人多かったかということである。 (第3段階)
このようなことは,初めは,どうしても教師が中心になって練習させるようになるであろう。しかし,練習を積むにつれて,こども自身で,どんな問題にぶつかっても,いつも,今まで述べてきた三つの段階を通って問題を分析したり,分析したものをまとめたりすることができるようになるであろう。このようなことができるようになって,はじめて,書かれた問題を解決するための論理的な思考の進め方が,こどもの身についたということができるのである。
(3) この指導計画は,どんなねうちをもっているか
これまでは書かれた問題を解決するための思考の進め方を中心にして,論理的な思考力を伸ばす指導計画について述べてきた。その指導計画は,次のようなねうちをもっていると言える。
(a) 第一の段階において,数や記号などについての話合いをしないで,一つの物語りの筋をまとめるように考えると,問題の場の全体を容易に理解することができる。
(b) 問題の場について,話をさせたり,問題の場を文章に表現させて記録させたりすると,こどもの用いることば,特に,用語を改善していくことができる。
(c) ものごとの筋道をたてて考えるようになる。また,答える場合でも,筋道をたてて考えたことを答えるようになり,答を思いつきや,あてもの式に出そうとはしなくなる。
(d) 事がらを分析したり,組織だてたりして,問題の場を全体としてつかむことがじょうずになる。また,そのような行為が習慣にまで高められる。
(4) 第一段階の書かれた問題を解決するための段階
問題を解決する能力を伸ばすには,論理的な思考力を伸ばすことがたいせつである。それには,一つとして,書かれた問題を解決するにあたって,問題を解決するための思考の段階を考えて,秩序正しく考えを進めるように指導することがたいせつである。これは,今までに述べてきたことである。
ここでは,今までに述べてきたことを合わせて,例を一段階の書かれた問題の解決にとり,問題を解決していくときに,どんな段階があるがを具体的に述べてみよう。
① 問題を読む
② 何についての問題であるかを明らかにする
③ どんな事実が与えられているかを明らかにする
④ 何を求めればよいかを明らかにする
⑤ どんな演算を用いたらよいかを明らかにする
⑥ 結果を推定してみる
⑦ 推定することができたら,計算する
⑧ 結果を確かめる
このうちで,①から④までについては,今までにその考えの進め方や指導の方法について述べてきた。これは,今までの問題解決の指導において,特に弱いところであると考えられるからである。したがって,今後の指導において,じゅうぶん注意してもらいたいと考える。
⑤から⑧までの段階については,今まで,問題解決の指導において,指導されてきているので,ここに改めて,その考え方や指導の方法を述べるまでもないことであろう。ここでは,考えを進める段階を述べておくだけにとどめよう。ただ注意しなければならないことは,今述べた段階は,すべて一段階の問題を解決するためのものであると,簡単に考えてしまってはならないということである。この考えを進める段階は,二段階の問題を解決する場合においても,これに準じて考えるのに参考になるであろう。
問題解決の指導において,このような論理的な考えの進め方が,だんだんにこどもの身につき,やがては,こども自身が,どんな問題にぶつかっても,論理的に考えていくようにしたいものである。
以上は,例を書かれた一段階の問題にとって,論理的な思考力を伸ばす計画や方法について述べてきた。これは前がきにも述べたように,日常生活において起る問題をよりよく解決する能力を伸ばすためのものである。
この究極のねらいを忘れて,論理的な思考力を伸ばそうとして,先に述べた段階を指導しても,その指導は形式的になり,そのねらいを達成することができないであろう。
また,問題解決の指導において,あてもの式でなく,問題を分析して,その筋道をたて,問題のありかを論理的に明らかにするとともに,問題を解決する能力を身につけ,このようにして,論理的な思考力を伸ばそうとしていることにじゅうぶん注意してもらいたい。
5.個人差に応ずる指導計画
| 個人差に応ずるためには,どのように指導計画をたてたらよいか。 |
算数の学習において,こどもの個人差に応ずるように指導するには,どんなことに注意して計画をたてたらよいかを考えて,その目のつけどころのおもな事がらを具体的な例について説明してみよう。
個人差に応ずることができるようにするためには,教師の立てる計画は,大きく次の三つに分けて考えることができる。
○クラスの指導計画
○グループの指導計画
○個人の指導計画
この三つの指導計画について,教師が指導をするにしても,こどもが学習したり,また,その結果を確かめたりするにしても,いつも,めいめいのこどもの自主性を高めていくように学習を組織するように心がけなかったら,どれも学習の効果をあまりあげることができないと考えられる。しかも,この三つの計画に分けてあるが,指導計画は,この三つのものを組み合わせてできるものである。
なお教科書を用いるとしても,どのこどもにも適している場合にだけ,クラス全体の指導に用いることができる。また,特殊のこどもたちの必要に応じているときには,そのこどもたちを一つのグループに作り,このグループの指導に用いることができる。また,特定のこどもの練習,計算の確かめなどに適しているときには,そのひとりの特定のこどもの指導に用いるがよい。
(1) クラスの指導計画
学級が同じであっても,その学級のこどもがそれぞれ異なった能力を持っているからには,いつも同じ事がらについての反復練習とか,あるいは,同じ仕事をしているというのでは,どのこどももその学習に参加するというわけにはいかない。したがって,どのこどもにも満足する学習効果が得られるというわけにはいかない。そこて,こどもがひとりびとりの能力に応じて学習できるように,指導計画をたてることが必要になってくるのである。
たとえば,学級の中の遅れたこどもには,最少限の仕事を割り当てる。並みのこどもには,それにさらに仕事をつけ加えるようにする。また,ずば抜けて優秀なこどもには,もっと内容の豊かな学習活動をとりあげるなどして指導計画をたてることが,これにあたる。
例を,単元「郵便屋さん」について述べてみよう。
この単元のねらいは,こどもがはがきなどを作って,それにたよりを書いたり,郵便屋さんになったこどもがそれを集めたり,配ったりするなどして,郵便の機能について理解をもたせることにあるとしよう。例をこの単元の展開にとり,上に述べたクラスの指導計画の一つの実際例を示してみよう。
学級のこどもで,遅れているこどもには,はがきを作ったり,それにたよりを書いたりするというような,最少限の仕事を割り当てるのである。並みのこどもには,はがきのほかに封書を書いたり,また,封書にも,クラスに両親を招待するといったねらいをもった仕事をするというように,遅れているこどもの仕事に,さらに仕事をつけ加えるように計画をたてるのである。
さらにずっと進んだこどもであると,その封書の目方をはかって,郵便料金を計算したり,郵便の歴史についての簡単な調査をして報告したりするといった,程度の高い学習活動をとり上げるように計画をたてるのである。
このようにすれば,こどもが,めいめいの現在の状態からみて,これに適したそれぞれの学習活動を選択することができる。このように,指導計画を準備しておくことが必要である。
上にあげたのは,単元の仕事の割り当て方の例であるが,指導計画を個人差に適合させる方法は,これに限ったものではない。場合によっては,学級のどのこどもも,同じような仕事を始めることもあるだろう。また,時には,ひとりびとりのこどもが,それぞれの能力にふさわしい仕事を選択することもあるだろう。
単元の学習の途中で,ある特定のこどもに,そのこどもが当面している困難を克服していくように指導する必要のある場合もあろう。時には共通の困難を感じているこどもを教室の一すみに集めて,話合いをしたり,発表させたりしているうちに,そのこどもに共通な困難を明らかにしたり,その困難を克服していくための手がかりを与えたりすることもあろう。
また,場合によっては,クラス全体のこどもが,いっせいに仕事を中止して,仕事がどこまで進んだか,どんな点がうまくいったか,どんなことが困難であったか,それをどんなに解決したか,あるいは,これから,その仕事をどんなに発展させていったらよいかなどを,いっしょに話合いすることもあろう。そのあとで,また,何人かのこどもがより集まってグループを作り,測定や計算の結果などを確かめ合うことが必要になる場合もあろう。
以上述べてきたように,クラス全体に対する計画は,時に,全体での話合いをしてみたり,時に,ひとりびとりのこどもに特別の指導をしたり,さらに時には,グループにまとめて指導するというように,こどもの必要に応じて指導できるように,たてられねばならない。
なお,単元の学習においては,教科書の教材をとり上げて,それで練習をくり返すなど,指導の能率をあげるようにくふうすることが必要であろう。
また,教師が作るテストや練習問題などについても,その紙に答をじかに書かせないで,できるだけ他の紙に書くことにして,問題用紙が,いつでも必要に応じて,他のこどもにも使えるようにしまっておくようにすることも,一つのくふうであろう。このようなくふうをしていけば,教師の労力を節約し,指導の時間をより多く生み出すことができ,しかも,個人差に応ずる指導が有効にできるようになるであろう。
(2) 個人の指導計画
学級のこどもに能力の差があることが明らかになれば,どのこどもにも同じような仕事を与えて,これを同じように扱ったり,また,同一の時間にその仕事を完成させようと考えることはなくなるであろう。教育を個別化するということは,仕事の速いこどもは速いなりに,遅いこどもは遅いなりに,ひとりびとりのこどもが,めいめいの速さで進歩できるように指導することである。教師はこどもの学習の様子を見回り,その必要に応じて,ひとりびとりのこどもを指導するように心がけることが必要になってくる。
しかし,そのひとりびとりに対する指導も,思いつきや、その場だけのものであると,指導の効果はあまり期待することができない。このような意味からも,計画的な処置や準備をすることが必要になってくるのである。
次に,個人に対する指導計画をたてるためには,どんな処置や準備が必要になるかについて,そのおもなものをあげてみよう。
(a) ひとりびとりのこどもが,どんなことはできるかを書きとめておくようにする
ひとりびとりのこどもについて,教師は,学習の進度表のようなものを用意しておき,それに,そのこどもが,どんなことは理解できているか,また,どんなことについての理解はふじゅうぶんであるかなどが,一見してわかるように記録しておくのである。たとえば,かけ算の指導について述べるならば,乗法九々,位取り,繰上がり,交換の法則などと,項目を設けておき,その項目の一つ一つについて,○や×で記入しておくのもよい。このような表を作っておけば,ひとりびとりのこどもに対し,計画的に指導することができるのである。単なる思いつきなどによったのでは,その指導が計画的でないために,一時的なものとなり,指導の効果を期待することができないであろう。
(b) あるねらいに到達しているかどうか,到達していなかったら,どこに原因があるかを知るために診断テストを用意しておく
このようなテストは教師が作る場合もあろうし,購入する場合もあろう。それらのテストを教室に備えつけておき,必要なときに,必要なこどもに実施するようにするのがよい。前項で述べたように,テストの答を他の紙に書くようにすれば,そのテストを何回も使うことができよう。また,テストの結果は,前に述べた進度表のようなものに記録しておくのがよい。
(c) 自習のため,あるいは自分の学習の誤りを自分で直していけるようにするため,必要な教材を準備しておく
高学年のこどもでも計算の誤りの原因を調べてみると,加法九々や減法九々,あるいは乗法九々などの基礎的な事がらについての記憶違いなどが原因となっているものが多い。このような誤りをなくするためには,低学年や中学年でよく練習しておき,正しく使えるようにしておくことがたいせつである。しかし,このようなこどもが全くないとはいえない。このような場合には,カードの表には「7+4」裏には「11−4」と書いておく。このようなカードを一そろいずつ箱の中に入れておく。こどもはどちらかを見て,その反対側で答を確かめる。正しくできた九々のカードは,箱の実のほうに入れる。誤った九々のカードは,箱のふたのほうに入れておく。これからあと,誤ったカードだけについて,正しくできるようになるまで何回も練習をする。こどもがひとりびとりで練習してもよいし,時に同じ必要を感じているこどもをグループにして,そのグループで練習するようにすれば,こどもの興味もいっそう増してくるであろう。このような教具によって,こどもは興味を持って自習をすることができるし,また,自分の学習の誤りを自分で直していくことができる。
以上は,個人に対する指導計画をたてる場合に,必要な処置や準備について述べたものである。
先に述べたように,教科書を使って教師の時間と労力をできるだけ有効に使うようにすることが必要である。ここでは,教科書を個別指導に使うときに,留意したらよいと思われる点について述べることにする。
(a) 仕事の割り当てに対する手びきを準備する
いわば,理科でいう実験書のようなものである。これにはひとりびとりのこどもの能力に応じた仕事の内容がわかるようにしてある。たとえば,一つの問題を解決するためには,どんなことを調べたらよいか,どんな計算をしたらよいか,どこの練習をしたらよいかなどがわかるようにしておくのである。それによって,こどもは自分がこれからどんな仕事をしたらよいかがわかり,自分ひとりでも学習を進めることができるようになる。しかし,この手びきを初めから与えておくことは,こどもが仕事の計画をたてるのに制限を加えることになるかもしれない。このことには,注意しなければならない。こどもが,これからの学習の計画ができたところで,このような手びきを与えるのがよいであろう。また,このような手びきがあまり親切すぎると,こどもの創意くふうをそこなう結果になるので,この点にも注意することが必要である。
(b) 補足的な説明をしたり,こどもが実際にためしてみるための教材や教具,診断のためのテストなどを準備する
こどもが,これからどんなことを,どんなに学習したらよいかを、決定するために,教科書はよい参考書であるに違いない。しかし,多くのこどもにとっては,単に教科書を読んだだけでは,これから自分がどんな仕事をしたらよいかとか,どんなことについて学習したらよいかを決めることが困難であろう。そのようなこどもに対しては,前に述べたような手びきも有効である。こどものなかには,簡単な助言によって,あとはひとりで学習していけるものもあろう。具体物や半具体物を使って実際にやってみないと,簡単に理解できないものもあるだろう。このようなこどもに対しては,実際にやってみるために必要な教材や教具を準備しておいたり,適切な助言を与えたりすることが必要である。また,めいめいのこどもが教科書のどこを学習してよいかを明らかにするために,診断のためのテストを準備しておくことも必要である。また,こどもが学習できたところで,自分はどんなことがわかったか,あるいは,まだどんなことがわからないかを評価するために,教科書のどこを練習したらよいかとか,また,そのために必要な助言も考えておかねばならない。
以上は,教科書を個人指導に使用する場合に必要な処置や準備について述べてみたのである。
なお,個人指導の場合には,教師は,特に,自分の労力をできるだけ節約して,これをより有効な指導に使えるようにくふうしなければならない。たとえば,何人かのこどもが,ほとんど同じ時に,同じ新しいことについて学習ができるようになった場合には,これらのこどもを1箇所に集めて,こどものやった仕事や計算の方法などについて発表させたり,これについて話合いをさせたりして,それらをもとにして,これまでの学習に対する指導をするのである。このようにして,今後の学習についても示唆を与えることが必要になってくるであろう。また,時には,何人かのこどもが同じような困難や混乱に当面していることがある。このような場合には,これらのこどもを教室の一すみに集めて,どこに困難があるか,今まで,これに似たような問題を解決したことはなかったか,その問題と今の問題とどんなところが似ているかなどについて話合いをするのもよかろう。このように必要に応じて,グループにまとめて指導するようにすれば,個人に対する指導の能率をいっそうあげることができるであろう。
また,教師の労力を有効に使うための一つの方法として,能力のあるこどもを教師の補助にする場合もあろう。たとえば,すでに一つの学習が終ったこどもを,まだそれを学習している他のこどもたちの援助者にしたり,リーダーとするのである。
このように,こどもが,自分の能力に応じて,それぞれの仕事をするように学習の計画をたてておき,こどもが自分の力にふさわしいことについて,学習をすることができるようにしておかなければならない。
(3) グループの指導計画
ここでとりあげているのは,算数についての指導のためであるから,主として能力別のグループ学習の指導についてのものである。すなわちほとんど同じ能力をもっているこどもを集めてグループを作り,それぞれのグループごとに指導を進めることについてである。これは,先にあげた個人指導の能率をいっそうあげるために考えられたものである。
このグループの個数は,だいたい三つというのが普通である。グループの数を四つ,あるいはそれ以上にすると,指導をする上に,非常に困難であるといわれている。
グループによる指導は,個人に対する指導と同じように,周到な計画のもとに進められる必要のあることはいうまでもない。次に,三つのグループに分けた場合に,指導をどんなに進めたらよいかを,例について説明しよう。
まず,第一のグループは,ある新しい単元か,または新しい演算について勉強し始めているとしよう。教師はその学習の一時限を,三つのグループに,等分した時間ずつ指導する必要はない。このような新しい学習をしているグループに対しては,その指導に多くの時間をかけなければならないだろうから,必要に応じて計画をたてるのが普通である。もちろん一時限の間に,三つのグループのどれもが,一度は指導を受けるように計画する必要はある。とにかく,どのグループも同じ時間だけ指導することは,必ずしも指導の能率の上がる計画とはいえないであろう。きょうは第一のグループ,あすは第二のグループというように,新しい困難の多い学習をするグループを計画的に決めておき,そのグループに対しては,他のグループよりも特に多くの時間をかけて指導できるように,計画をたてることが必要である。
次に第二のグループは,先に学習したことを応用したり,あるいは必要なことについて自習したりしているとする。このような学習をしているグループに対しては,教師はこどもの仕事を見回ってみて,特に指導の必要がある何人かのこどもに指導する時間があればじゅうぶんであろう。たとえば,前に学習したことを忘れているこどもとか,あるいはまちがって記憶しているこどもとか,何かの原因で誤って計算などしていてもこれに気づかないでいるこどもとか,困難にぶつかってどうしてよいかわからないでいるこどもなどに対して,暗示や手がかりを与えたり,簡単な指導をしてやればよいのである。
第三のグループは,前に学習したことについて反復練習をしているとする。こどもは,めいめいの能力に応じて,正確に速くできるように練習をくり返している。このグループに対しては,こどものできぐあいを調べて,簡単な評価をしてやったり,仕事の確かめが終ったこどもには,この練習ができたところで,どんな類型のものについて練習したらよいかを指示すればよい。したがって,このグループに対する指導の時間は,短くてじゅうぶんであろう。
以上は,第一のグループは理解や実際にやってみる段階の学習であり,第二のグループは練習の段階の学習であり,第三のグループは反復練習の段階の学習である場合について述べたのである。
グループの仕事をきめる場合の他の方法について次に述べよう。それはある単元の問題に関係のある算数的な仕事を,クラス全体で計画しているときである。一つ一つのグループは,仕事の責任を分担して,学習を進めるように計画をたてるのである。たとえば,第一のグループは遠足の旅費を算出するために,汽車賃やバス代について調べている。第二のグループは,遠足の日程を作るために,汽車やバスの発着時刻を調べている。第三のグループは,遠足の目的地やその附近の産物などを調べて,自分たちの郷土と比べて,これをグラフや表などにまとめている。このように遠足という一つの共同問題に対して,それぞれのグループが仕事を分担して学習を進める場合も考えられよう。
ここで,一般に,グループに対する学習指導の計画をたてるときに,考慮しなければならないたいせつな事がらを述べることにする。
仕事の割りふりは,グループごとに定めておくようにする。進んだこどものグループに対しては,技能の練習が早く終るであろう。このグループのために,その他に,補充問題,数学についての研究,もっと進んだ研究をするための読み物,その他の課題などについて学習できるようにしておくことが必要である。また,時には,さらに発展して,学級の仕事ばかりではなく,学校全体のこどもの身長や,体重,胸囲などが年々にどんなに変化してきたかとか,あるいは学校給食が始まってから,毎月の体重がどんなに増加してきたかなどを表やグラフに表わして,廊下などに掲示しておくようになるなど,学校全体の仕事を興味をもって積極的にするようにもなるであろう。このように計画をたてておけば,進んでいるこどもは,ますます自分の能力を高め,学習を掘り下げていくことができる。また,そのこどもは,創意を用いて仕事をするようになり,他人にたよらないで,自分の力で仕事をしようと努力するようになるのである。
これに反して,おくれているこどもに対しては,できるだけ簡単で,しかも,最少限の仕事を割り当てるようにすることが必要である。このグループのこどもに対して過度に負担をかけると,こどもは決して学習に成功することができない。このこどもにあまり多くの仕事を割り当てるようにすると,かえって学習をいやがる原因になることもある。むしろ,できるだけ少ない分量の仕事を与え,こどもが学習に成功できるように計画をたてるのである。しかも,それだけでもできたときには,教師は惜しみなくほめてやるのがよい。それによってこそ,このグループのこどもは学習に自信を持ち,その成功感によって,次の学習への意欲が強められるのである。そのためには,できるだけ基礎的な技能を習得できるように指導したり,また,それらの練習の機会を多く設けるように,教師はくふうすることがたいせつである。
以上述べてきたように,こどもたちをいくつかのグループにまとめて指導することは,こどもが個人差に応じて学習ができるようになるのと同時に,学習指導を能率的に進め,しかもその上に,こどもの協調的な態度を育成し,社会性をつちかうのにも,有効なものであるといえよう。
また,個人差に応ずる指導は,初めに述べたように,決して一つの型にはめて考えるべきものではない。場合によって全体に対して指導をしたり,時に個人指導や能力別グループ学習を指導するというように,必要に応じて計画をたて,学習指導を進めるようにすることがたいせつである。