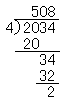Ⅳ.算数についての学習指導法
算数についてのこどもの学習活動は,どのように指導したらよいか。
教育愛に燃えた教師は,ひとりびとりのこどもの困難を知っている人であり,こどもをはずかしめる人ではなくて,いつでも必要に応じて,こどもに指導を与えることのできる人である。
Ⅳ.算数についての学習指導法
算数についてのこどもの学習活動は,どのように指導したらよいか。
第1部 一般的な問題
1.どんな事がらをもとにして,学習指導を考えたらよいか。
2.算数指導の上に,どんな変化がもたらされているか。
3.どのように指導したら,こどもが自主的に学習するようになるか。
4.どのように指導したら,こどもが理解をもって学習していくようになるか。
5.どのように指導したら,こどもが学習したことを使って,日常生活を改善することができるようになるか。
6.学習内容を,ひとりびとりのこどもに適応させるには,どのように指導計画をたてたり,指導したらよいか。
7.どのように,実際に適用することや,練習,反復練習を指導したら,算数を有効に用いることができるようになるか。
8.教科書を有効に使うには,どのようにしたらよいか。
第2部 特殊な問題
1.どのように診断的指導を用いることができるか。
2.反復練習をどのように指道したらよいか。
3.どのように指導したら,技能が必要に応じて,使えるように身についてくるか。
4.どのように指導したら,こどもの論理的思考を伸ばすことができるか。
5.個人差に応ずるためには,どのように指導計画をたてたらよいか。
第3部 望ましい計算方法の案
第4部 幼稚園および低学年の指導
第1部 一般的な問題
1.学習指導法についての基本的な事がら
| どんな事がらをもとにして,学習指導法を考えたらよいか。 |
ここでは,学習指導法をくふうするときに,どんなことをもとにしたらよいかを考え,その基本となるものをあげてみることにする。
(1) 学習指導と個人の尊厳
どのこどもも,めいめいが特別の必要,能力,興味をもっている個人である。この個人こそ教育的な営みの用心となるものである。この教育的な営みによって,こどもがめいめいの一生をとおして,社会における責任を果すように,めいめいの責任の自覚をうながし,その責任を果すことによって深められる個人の尊厳をつちかうように,適当な教材と方法を用いて,指導が行われなければならない。
(2) 学習指導と個人差
これは,どんな学習指導法を考えるときにも,考慮しなければならないことである。したがって,算数についての指導でも当然考えねばならないことである。しかも,これは学習指導法について考えるだけでなく,指導内容やまた,算数科の目標を考えるときにも,考慮に入れなければならないことてある。これについては,さきに第Ⅱ章の算数科の目標や第Ⅲ章の指導内容のところで述べたとおりである。
こどもの行為は教師の目から見ると,いろいろな内容をあげることができる。たとえば,こどもが物の売買をしているとする。「ことばを正しく使って,物やそれを買入れる個数を言い表わすことができるか。」などの国語についてのねらいからも,ながめることができるであろう。また,「おつりを正しくもらうことができるか。」とか,「おつりを出しやすいように,おかねを出すことができるか。」などの算数についてのねらいからも,ながめることができるであろう。そのほかに,いろいろな教科にあげてあるねらいからも,ながめることができるであろう。しかし,これは教師の目から見てのことであって,こどもの立場にたってみると,ただ物の売買をしているにすぎないのである。一般にこどもの行為を,教師の立場から見ると,いろいろに分析してみることができるが,こども自身にしてみれば,そんなばらばらのねらいをもっているものではない。内面的に統一され,目的をもった活動をしてるにすぎないのである。もしも個数を数えたり,計算したり,測定したりすることが,目的のない,いわばこどもの盲目的な活動として,統一の欠けた個々ばらばらのものとして指導されたのでは,こどもの生き生きとした学習活動を期待することができない。また,こどもの日常生活で生きた能力とはならないであろう。学習指導計画は,こどもがいつも目的を持って常に活動をするように,統合された経験を積み重ねながら進歩していくように,たてることが必要である。しかも,その進歩の様子は,こどもによってまちまちである。したがって,指導計画はめいめいのこどもが,自分の能力に応じて,進歩していくことができるように,くふうしなければならない。これで,はじめて,めいめいが自分の責任を果すことができるのである。
(3) 学習指導の対象
従来,とかく,算数については,計算や測定などのような,いわゆる数学的技能を形式的に指導しさえすればよいと考えられがちであった。それは,このような技能が,算数指導において,重要な領域の一つであることを示すものであるが,その指導さえも,じゅうぶんでなかったためであろうと考えられる。しかし,望ましい算数についての学習指導としては,単に基礎的な技能を形式的に指導するだけで,じゅうぶんであるとはいえない。
計算や測定などの技能が,いろいろな学習の場において指導され,また,有効に用いられるようになることは,賢明な一般国民として必要欠くことのできないことである。数量関係を用いてする判断や批判をする能力を伸ばすところまで考えられなければならない。
たとえば,百分率,グラフ,概数などについて指導するときに,単にそれらについての計算ができるだけでは,じゅうぶんであると言えない。これからさらに一歩進んで百分率やグラフ,概数を使って物を考え,判断したり,批判したりする能力が伸びていくように指導されなければならない。このためには,教師は,こどもの基礎的な数学的技能を用いる能力や望ましい態度などがだんだんにできあがっていくように,努力しなければならない。また,数的な資料について学習したこどもは,示されたグラフから数値を読みとったり,主要な傾向を読みとったりすることができるだけではいけない。このグラフはどんな目的のために,いつ書かれたものであるかを考えるようにしなければならない。また,その目的のために集められた資料や,その表わし方が,目的に対して適切であるかどうかも考えるようにしなければならない。さらに,そのような資料から得られた結論であってみれば,そのグラフによって示されている傾向は,どの程度に信頼してよいかも考えるようにしなければならない。これらのことについての判断をもとにして,そのグラフの示している事実や,それらに関連する事象について批判しようとするようになる。このように指導すれば,グラフから導き出されている結論を盲信するようなことはしなくなる。このようなことができてこそ,はじめて,こどもは個人の尊厳を知ることができるのである。
2.算数についての学習指導の変化
ここでは,算数指導法の改善に伴い,どんな変化がもたらされているかのおもなものをあげてみることにする。
(1) 算数は計算の反復練習だけをねらってはいない
計算の反復練習は,算数についての指導で重要なものである。しかし,それだけで算数科のねらいをじゅうぶんに達成することはできない。算数科が教育全般からみて,どんな部面を分担しているかについては,すでに第Ⅰ章,第Ⅱ章において大略を述べた。また,第Ⅲ章において,それに必要な指導内容を明らかにしてきた。反復練習は,算数についての習得された技能を,必要に応じて,なんらの抵抗なしに反射的に使うことができるようにするためのものであり,算数の指導から見て,一つの分野にすぎないのである。いわば,反復練習は,物事を判断したり批判したりするときに,気楽に使えるようにするための手段であって,それ自身がねらいではないのである。このような立場から,算数についての指導を改善しようとしている。
(2) 社会的な目標も重要である
算数についての指導において,数学的な目標を達成しようと努力しなければならないことは言うまでもない。しかし,それだけでは,じゅうぶんでない。社会的な目標も達成できるように努力しなければならない。
例を,おかねの取扱にとって述べてみよう。
数学的な目標だけから考えてみると,金高は十進諸等数の一つであるから,整数と同じように計算してよいことが分り,その計算ができるだけで,じゅうぶんであると言えるかもしれない。しかし,社会的な目標から考えてみると,おかねの有用さ,おつりやおかねの出し方,特に,おつりを出しやすいようにおかねを支払うくふう,さらにおかねをたいせつにして貯金することなどについての指導も必要になろう。これは単に個人の経済生活からみて重要なだけでなく,社会人としても重要なことである。このようなことについての指導を無視して,おかねの計算だけを形式的に指導したならば,その指導の意味の大半は失われてしまうであろう。
これと同じことは,時間についての指導についても言える。時間についての計算は,数学的な目標だけからみると,不十進諸等数についての計算法を指導すればじゅうぶんであると言えるだろう。しかし,社会的な目標からみると,これだけでは,ふじゅうぶんなことがわかる。会合や約束の時刻を守ることがどんなにたいせつなことであるか,めいめいの時間を有効に使うことが,どんなにたいせつなことであるか,また,他人に時間をむだに使わせないようにうすることは,どんなにたいせつなことであるか,これらは,ともに,道徳的感情の基盤となるものであり,めいめいが自分の時間をじゅうぶんに活用し,浪費しないようにすること,また,他人の時間を尊重することは,一般社会人としての責任であり,社会の発展に大きな関係をもっていることである。
このような社会的な目標をはなれて,算数についての指導をしたならば,望ましい人間育成を目ざしている算数科の目標をじゅうぶんに達成することはできない。このような意味から,算数指導についての改善が考えられてきている。
(3) 必要な既往経験を準備する
たとえば,乗法九々を指導しようとするときに,九々の唱え方や,乗法記号等を指導する前に,あらかじめ,同数累加を必要とするような実際の場に当面させ,「倍」についての観念の素地を豊かにしておくことが必要である。このような素地のないところで,九々を形式的に指導したところで,乗法の意味をこどもが理解することのできないのはいうまでもない。九々にはどんなよいところがあり,それがわれわれの日常生活に,どんなに有効であるかをわからせないでは,九々を日常生活に生かして用いる能力を伸ばすことのできないのは明らかである。ただ,九々が機械的に反射的に唱えられるようになるにすぎない。
小数の指導についても同様なことが言える。この指導に先だって,小数を用いての測定値の表わし方についての経験を豊かにし,小数点を必要とする多くの場に当面させて,1よりも小さい数についての素地を豊かにすることが必要である。このようなことについての考慮なしに,小数についての指導をしたとしても,単に小数についての計算をすることができるようになるだけで,小数をうまく実際の場において使いこなすまでに指導することができないであろう。
一般に,指導にあたっては,それに先だって,その指導しようとする内容についての数量的な既往経験を豊富にし,学習の素地をつちかっておくことが必要である。このような素地なしに指導をしたら,単に抽象的な計算や測定の方法や,記号や法則だけを,こどもに記憶させることになるであろう。このような意味から,算数指導についての改善が考えられてきている。
(4) 反復練習が必要である
こどもは,計算や測定などを一度学習しただけで,そのあと練習をしないでいて,その学習した技能を維持しつづけていき,必要があったら,これを自由に使いこなせるものではない。これは,ごどもについて言えるだけでなく,われわれおとなについても言えることである。学習した技能を維持し,これを身につけておき,実際の場に適用することができるようになるためには,その技能についての有効適切な反復練習が必要である。
反復練習を有効適切に指導する方法については,第2部の特殊な問題のところで,詳しく述べることにする。
さきに述べたように,従来とかく算数科は,まず,計算其の他の数学的技能を授け,次に,これを反復練習しさえすればよいと考えられていた。しかし,その反復練習は,あまり好ましい成績をあげたとは言えない。反復練習を必要とするものと,そうでないものとの区別を考えないで反復練習をさせたり,じゅうぶんな効果をおさめて,これを用いることに抵抗を感じなくなるにさきだって,反復練習が中断されたり,また,反復練習が技能の導入や理解のための指導に比べて低次な学習のようにさえ考えられていた。最近漸く反復練習についての指導が,算数指導全般から見て,どんなねらいをもっているかが明らかにされ,その指導の方法が科学的に研究されるようになったことは一大進歩といわねばならない。このような意味からも,算数指導についての改善が考えられてきている。
以上は,今日の算数指導を改善しようとして,どんな変化がもたらされてきているかを,その主要なものについて述べたのである。このような改善をしていくときに,どんなことに注意したらよいかを,これに続いて,くわしく述べることにする。
3.自主的な学習
| どのように指導したら,こどもが自主的に学習するようになるか。 |
ここでは,こどもが自主的に学習していくようにするには,どんなことに注意したらよいかについて述べることにする。
(1) こどもの現在のようすや困難を明らかにしてやる
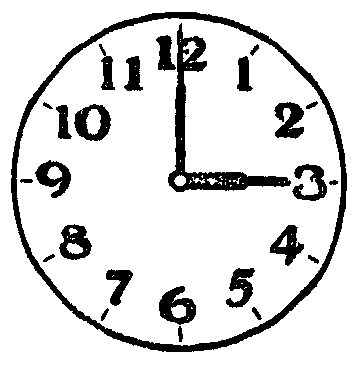 |
二年生のこどもに,とけいを使って,5分くぎりで時刻を読む方法を指導する場合について述べてみる。
一年生で「ちょうど何時」である場合について,とけいの読み方を指導したとする。そこで,まず考えられねばならないことは,こどもが一年生で指導したことができるかどうかをたしかめることである。この場合に,ちょうど3時,ちようど4時,ちょうど5時である場合に,とけいを読むことができるかどうかを確かめるのである。しかもその場合には,長い針はいつも12をさしていて,短い針は1から12までの数のどれかをさしていて,その短い針のさしている文字がちょうど何時であるかを示していることが,はっきり理解されているかどうかも確かめることが必要である。このようなことを,はっきり確認したところで,次の指導にうつるのである。 |
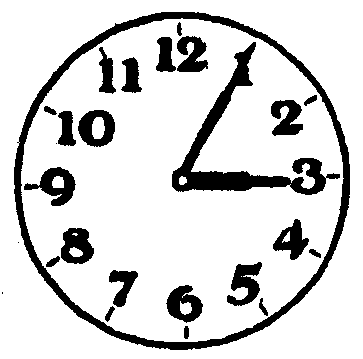 |
「何時」であるかを決めるのは,短い針であるとすると,左の図のように短い針が3を少し通りこしている場合には,何と読んだらいいだろうかを考えるように指導するのである。 |
こどもは,「3時半」とか,「3時すぎ」とか,「3時5分すぎぐらい」とか,いろいろと答えるであろう。そこで実際のとけいについて,ちょうど3時から4時まで針を動かしてみる。すると長い針がだんだんにまわって,一回まわると短い針が3から4までまわることを知るのである。そこで,「短い針でちょうど3時をみるのはよいが,3時からどれだけ過ぎたかを,短い針から読むことはむずかしい。そこで,これを読みやすくするために,長い針がつけてある。長い針が次の文字のところまでいくのにかかる時間が,いつでも5分である。」ことを指導していくのである。
このように指導していくと,長針が何のために必要であるかがわかり,とけいの読み方をまちがえることはなくなるであろう。
これに反して,いろいろな時刻を示しているとけいの絵を見せて,その時刻を言わせたとする。すると,短針と長針との関係を明らかにすることもできず,3時55分を4時55分と見あやまるようなことができてくる。
これは,自分の今までに知っていることとの関係から,どんな困難が起るかを明らかにしないで,その5分くぎりの読み方を,今までの指導と全く切り離して独立に指導したからであり,こどもに考えさせることをしないで,事がらを教えこもうとするところから起るのである。
一般に,こどもがどんなことはわかっていて,その上からみてどんなことはわからなくなってくるかを明らかにすることによって,こどもは自分で考えていこうとするものである。言い換えると,こどもは自主的に学習していくようになるのである。
(2) 困難なことがらを,一つずつ取り上げて解決していく
3年生で銀行ごっこをして,預金や払出し,残金などを表に書きこむことなら,おかねの出入りを記録する表についての理解や,370+80とか,450−180といった,繰上がりや繰下がりのある二位数の加減を指導しようとする場合について考えてみよう。
これを銀行ごっこをするのであるからといって,表の作り方を考えさせたり,加法や減法の計算方法を考えさせたりするのを,同時に取り扱おうとすると,こどもは自主的に学習していくことができない。もしも同時に指導するとしたら,おかねの出入りを記録するには,どんなことを書いておいたらよいか,また,これをどんな形式にまとめたらよいか,さらに,加減の計算はどのようにしたらよいかなどを一時に考えることになり,これらのものを分けて考えていくことのできないこどもは,混乱してしまうからである。いわば,教師が解決の方法をこどもに形式的に与えねばならなくなるからである。
このようなことの起らないようにする一つの指導のしかたを述べてみよう。
こどもと銀行ごっこをすることに話がきまったら,まず,銀行ごっこが順調に進むようにするために,どんなことができなければならないかを話合い,これを解決するための計画を立てる。そこで,,預金や払出しの期日や金高を忘れないようにするために,おかねの出入りを記録したり,計算がまちがいなくできるようにするために,何百何十円と何十円をよせる計算や,何百何十円から何百何七円をひく計算が正しくできるようにすることが必要になるであろう。
このように,解決しなければならない問題がはっきりしてきたところで,これらのうちから問題を一つずつ取り上げて,学習を進めていくのである。
たとえば,はじめはおかねの出入りのようすを,きちんと書き残しておくには,どのように書いておいたらよいだろうかを学習することにしたとする。そこで,学習のきっかけを作るために,次のような例を述べてみることも考えられる。
1.5月16日に,20円あずけ入れてきました。
2.5月19日に,また70円あずけました。
3.5月25日に,50円引き出しました。
4.5月28日に,40円あずけました。
こどもは,めいめいに,これをどのように記録しておいたらよいかについてくふうするであろう。めいめいのくふうが一応できたところで,その方法を発表してもらって,これらを比較検討していく。
Aさん
| 5月16日に20円あずけました |
| 5月19日にまた70円あずけま |
| した。5月25日に50円 |
| 引き出しました。 |
| 5月28日40円あずけました |
Bさん
| 5月16日 20円あずけた |
| 5月19日 70円あずけた |
| 5月25日 50円引き出した |
| 5月28日 40円あずけた |
| |
Cさん
|
月日
|
あずけた
|
引き出した
|
|
5.16
|
20円
|
|
|
19
|
70円
|
|
|
25
|
|
50円
|
|
28
|
40円
|
|
Bさんの記録は,Aさんのに比べて,一日分が一行ずつに書いてあるのでわかりやすい。また,Cさんの記録はBさんのに比べて,あずけたおかねと引出したおかねが別の欄に書いてあり,わざわざ,あずけたとか,引き出したなどと、ことばで説明する必要がない。したがって,すっきりとわかりやすく,書くにも簡単である。このようなところまでまとめてきたとする。さらに進んで,いつも,いくらあずけてあるかがわかるようにするには,どうしたらよいかについて話を進めていく。このように学習を進めていくと,下にあるような表が,どのようにして考え出されたか,また,どんなよいところがあるかなどを,手がたく指導していくことができるであろう。このように指導していけば,こどもが最善をつくしさえすれば,一つ一つの困難を順次に解決していくことができる。
このようにして,おかねの出し入れの記録のしかたがわかったところで,加法や減法の計算の方法の指導にはいるのである。このように,困難を一つずつ克服していくように指導の計画をたて,こどもが最善の努力を払いさえすれば,成功できるようにしていくならば,こどもは自分の学習の目標をはっきりとらえて,迷うことがないから,こどもが自主的に学習していくようになる。
(3) 具体的なものを使って,こどもに目標をはっきりつかませる
これを,具体的な例によって説明してみよう。五年生のこどもに「84個入りのりんご一箱を,1個について12円の割で仕入れ,箱をあけてみたら,8個はくさっていた。くさっていないのを1個15円で売ると,全体ではいくらのもうけになるか。」の問題を解決することを指導するとしよう。
こどもの中には,すぐに解決できるものもあるだろう。しかし,できないでいるこどもはその問題の場をはっきりとらえることができないのである。そこで,次のような方法をくふうしてみるのである。
おはじきや小石などを使って,84個を並べてみる。その中の8個だけがくさったものとして,白いチョークでしるしをつける。このようにして目で見たり手で数えてできるような具体的なものになると,こどもは,その問題の場をやさしくとらえることができ,その目標をはっきりとらえることができるので,自主的に学習を進めていく。単に教師の口先きで説明するだけでなく,具体的なものを使って問題をとらえさせることもたいせつなことである。
もう一つの例をあげて説明してみよう。2年生のこどもに,はがきを作らせる指導について考えてみよう。はがきは,たて14㎝,よこ9㎝の長四角である。これを作るのに,どこのところが学習の要点であるかを,こどもにことばだけで,はっきりとらえさせることは,そんなにやさしいことではない。このような場合には新聞などを使って,こどもに,はがきを作らせてみるのである。できたところで,みんなの作ったはがきを取り上げて重ねてみる。この場合に,みんながきっちりとした大きさにできているかどうかを比べるには,どうしたらよいかを発問してみるのもよい。さて,大きさがまちまちであったら,どれがきっちりときめられた大きさになっているかを調べたり,大きさがまちまちにならないようにくふうすることの指導にはいるのである。物さしの目もりを正しく読んで,14㎝と9㎝の長さをきっちりはかりとって,しるしをつけ,そのあとで,しるしをつけたところをきっちり結ぶ線を引き,その線にそって切ることの必要が,こどもの中から生れてくる。
一般に,こどもに,頭の中だけで考えさせたり,教師が口さきで説明したりするだけでは,問題の要点をつかむことができない。具体的なものを使えば,問題の要点をやさしく明らかにとらえることができ,学習の必要を感じてくるので,こどもは自主的に学習を進めていく。
(4) すでに学習したものが,これからの学習をするのにどんなに役だっているかをわかるようにしてやる
これも一つの例を用いて説明しよう。6年生で異分母の分数について,加減法の計算を指導する場合について考えてみよう。
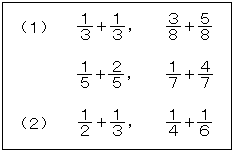
こどもに,下の(1)のような計算を復習したあとで,(2)のような場合の計算のしかたを考えさせる指導にはいることにする。
そこで「(2)はどうしてできないのだろうか。」とたずねると,「分母がちがうから。」と答えるにちがいない。また,「(1)はどれも分母が同じになっているからできる。」と答えるであろう。そこで「(2)ができるようにするには,どうすれはよいか。」と発問する。「(1)と同じように分母を同じにすることをくふうすればよい。」と答えるにちがいない。ここまできて,「1/2と1/3を,分母の同じ分数にすることはできないだううか。」と発問する。5年生の時に,分数の分子,分母に同じ数をかけても,同じ数で割っても,分数の大きさには変りがないことを学習したことを思い出す。こうした手続を経て,1/2を3/6に,1/3を2/6に変形することができることに気がつき,1/2+1/3=3/6+2/6に導くのである。
こうして,異分母の分数の加法は,分数の変形を用いることによって,同分母の分数の加法に導くことができることを指導すれば,通分することができれば,計算できるからといって,通分することだけに努力しさえすればよいことがわかり,自分の学習の前途に光明を見いだすのである。このようなことから,こどもは,自主的に学習を進めていく。
(5) 日常生活で必要になるものや興味あるものを使う
これも一つの例を用いて説明しよう。1年生の初めごろ,数字が順序を表わすことを指導しようとする場合に,数字が順序をきめるために有効に使われて,しかも,こどもが興味をもって学習する場を考えてみる。このようなねらいに適切なものとして,運動会のかけっこの等旗について指導することが考えられる。
こどもは,学校にはいって,大ぜいの友だちができ,みんなで活動することはこの上もないうれしいことであろう。また,運動場につれ出せば,だまっていてもかけだすのが健康なこどもの自然の姿であろう。そこで,かけっこのきょうそうをしよう。ということになれば,よろこんでやろうとみんなが参加してくる。その際,どのこどもが1等,どのこどもが2等であったかを,はっきりわかるようにすることを考える。すると,1等の旗,2等の旗を渡せば,はっきりわかることを納得するであろう。さて,1等,2等とやさしく区別ができるような旗は,どんな旗であるかを話し合うことにする。すると,数の必要がはっきりと理解され,数はものの順序を言い表わすのに役だつことを理解するであろう。
めいめいが,自分の等級に応じた旗を正しくにぎるには,数字をまちがいなく読むことが必要になる。このように,数が順序を示すのに便利なものであることを理解し,必要と興味がもとになって,学習するときには,こどもは進んで学習に参加しようとする気持を持ってくるものである。このようにいっても必要や興味は人によって違うことがある。たとえば,女のこどもはお人形遊びに興味をもつが,男のこどもは野球を好むように,男女によって異なることも考えておかねばならない。
もう一つの例をあげてみよう。6月ごろになると,急激に赤痢患者がふえてくる。ラジオや新聞などでも,夏の衛生について,やかましくいわれてくる。こどもは,赤痢という病気に対して関心をもってくる。といっても,1,2年のこどもには無理である。6年生ともなると,関心をもってくることは明らかである。それで6年生にこれを取り上げ,他の伝染病と比べて,どちらが多いか,何倍ぐらい発生しているかなどを考える。概数をとることや,死亡率を調べるためのわり算が必要になってくる。この場合に,四位数を五位数でわるような大きい数の比較的むずかしいわり算でも,関心が深いものであってみれば,その興味と関心とによって,自主的に調べようとする。そうした中で,自分の調べたいと思うことを算数が解明してくれることを知り,さらに,次の事実を調べてみようとする欲求が起ってくる。このようにして物事を研究するときの喜びを味わうことから,自主的に学習する習慣がついてくる。
このように,こどもの発達程度や地域や生活をよく考慮して,教材を選ぶことが必要で,単に教科書にあるから扱うといった態度はとらないようにすることがたいせつである。このようにすれば,こどもが自主的に学習していこうとするものである。
以上は,こどもが自主的に学習していくようにするには,どのように指導したらよいかを考え,その主要なものをあげて,これを具体的に説明したのである。
4.理解をもっての学習
| どのように指導したら,こどもが理解をもって学習していくようになるか。 |
こどもが算数を学習するとき,どうしてそのように計算してよいのか,その計算がどんな意味をもっているのか,また,その計算を用いるとどんな便利なことがあるかなどについて,理解をもつようにすることは必要なことである。これは,今までに何回となく主張してきたところである。もしも,こどもがこのようなことについての理解をもっていないと,こどもはその計算などを,ただ形式的にまねをしたり,暗記したりすることになってしまう。それだけでなく,学習したことがらの背後にどんな原理があるかとか,どんな関係があるのかがわからないので,単に個々のものをばらばらに記憶しておらなければならなくなる。また,その計算の方法を忘れてしまったり,他の似よった形式で書かれている計算との区別ができなくなって,混乱を起したりしやすい。また,形式的に学習した事がらは,これを一般に適用したり,いろいろな問題の解決に役だてることができなくなる。ここで,このようなことの起らないようにするには,どのように指導したらよいかを考え,その主要な目のつけどころをあげることにする。
(1) 既往経験を準備する
われわれが今日用いている計算などは,先人の長い間のくふうのたまものである。ところが,われわれは,その便利さになれきってしまって,ややもすると,それがどんなにすぐれたものであるかとか,日常生活で計算がどんなよさをもっているかなどが,わからなくなっていることが多い。このように,われわれがなれきっていることでも,はじめて学ぶこどもにとっては,そんなことはわからないはずである。それがどんな意味をもち,生活にどんなに役だっているかは,こどもに理解させることが必要である。
このような意味から,こどもに計算などを指導する場合には,それを使うことが必要になるような経験を,事前に準備してやることが必要である。
たとえば,棒グラフについて指導しようとする場合について説明してみよう。絵グラフでは,一つの絵がどれだけの大きさを表わすかを,決めてかからなければならない。さて,絵グラフを用いていくと,端下のある場合には,これを適当に処理したり,絵の分数部分を用いることが必要になる。そこで,量の大きさを詳しく表わすには不便であるような経験をもたせておく。これらの困難を解決しようとして,ここに棒グラフの指導にはいっていくきっかけを求めることができるとともに,棒グラフについての理解を,こどもがもつようになるのである。さらに,絵グラフでは,一つの絵がどれだけの大きさの量を表わすかをきめておいたが,棒の長さで表わすとしたら,どんなにしたらよいかが問題になってくる。ここで,縮尺のような表わし方も考えられるであろう。量の大きさを,棒の長さで読みとりやすくするために,軸に目もりをつけておくことが考え出される。このように,棒グラフを指導するには,それに先きだって指導してある絵グラフなどについての必要な既往経験を,よく準備しておくことが重要であり,これで,はじめて理解をもって学習していくのである。
もう一つの例をあげて説明してみよう。
二つの量の割合を表わす場合について述べてみよう。Aを基準にするとBがその整数倍になっているときには,わり算でやさしくできる。このように割合を表わしておくと,Bを基準にしたAの大きさを示す割合は分数で表わされて,その分数はもとの整数の逆数になってくる。このような既往経験を準備しておき,どちらも基準にとることができ,しかも,二つの量の割合が簡単にはっきりと言えるようにするには,比を使えばよいことを指導すれば,比の意味が,よく理解されるであろう。
一般に,ある事がらを指導しようとするには,あらかじめ,とれに必要な既往経験を持たせることを考えるとともに,これに関係のある必要な既往経験をまとめておけば,ここで指導しようとすることと,今までに学習した事がらとの関係が明らかにされ,ここにはじめて,こどもの理解の糸口がひらけてくるのである。
(2) 具体的な教材を用いる
命数法や記数法は,物の個数を数える場合の手続を,手ぎわよく一つの形式にまとめたものである。また,計算はいくつかのグループをよせ合わせたり,いくつかのグループに分けたりするときの手続を手ぎわよく一つの形式にまとめたものである。これらは,人類が生活を改善し,向上していくための道具として,日常の具体的な操作をくり返して,いろいろとくふうを重ねている間に考えついたものである。したがって,こどもに算数を学習させる場合には,どうしてそのように計算するようになったかが,こどもにおのずからわかるように,具体的な教材をとおして指導することが必要である。このような指導によって,こどもは計算についての理解ができるのである。
たとえば,32−17の計算が楽にできるのは,10ずつにくぎり,これを束にして数えたり書いたりするように組み立てた,十進法の位取り記数法のおかげである。そこでまず,この計算を指導する場合に,10本ずつを束にした割りばしを3束と,2本の割りばしを用意する。次に,それから17本を引かせるのである。7本をとることができないので,10本束をくずして,12本から7本をとる,このような手続から,繰り下がりのあるひき算のしかたを,やさしく理解することができる。
もう一つ,補数関係についての指導のしかたを述べてみよう。
10本の割りばしが並べてある。これからできるだけ早く8本をとらせるような操作をさせる。初めのうちは,1本ずつ数えて8本をとるであろう。こどもが次には2,4,6……と数えて8本とり,さらに早く8本をとらせると,2本だけ残して,直ちに8本とれることがおのずからわかってくる。こうした実際の行為をとおして,補数関係が明らかになってくる。
赤と白のはしを10本ずつ用意しておく。その中から赤白まぜて7本のはしをとらせると,こどもの中には,赤を4本,白を3本とってみたり,赤2本に白5本をとったりなどする。このような遊びのうちに,こどもは,おのずから数の概念を理解してくる。
以上のように,頭の中で考えていることを,具体的なこどもの仕事をとおすことにより,言い換えると,身体的な行為をとおしている間に,おのずから数量関係や演算について,こどもが理解するものである。
(3) こどもの年令や生活にふさわしい教材を選ぶ
教材がこどもの年令や日常生活にふさわしくない場合には,こどもは,その教材について理解をもつことができない。
たとえば,3年生の東京のこどもに,方向の言い表わし方を指導しようとして,ここからみて鹿児島は南の方にあるとか,また,青森は北の方にあるなどの例を用いたとしても,その土地に行ったことも,聞いたこともないこどもには,南や北の方向について理解することが困難である。
また,「100円の株500株を85円で買った。いくら支払えばよいか。」という問題を提出したとする。計算は,85×500としてやさしいものであるが,額面や時価についての理解がじゅうぶんにできないこどもにとっては,この問題についての理解をもって,考えていくことができない。
このようなことの起るのは,とりあげている教材が,こどもの年令や日常生活にふさわしくないからである。
(4) あやまりや誤解は,時機を見失わないで指導する
たとえば,小さいこどもは,とけいを読む場合に,8時50分を9時50分と読み誤ることがある,これは短針が文字板の8より9に近づいているために9時と誤解しているのである。また,8時30分の時刻を,模型のとけいで示させたり,紙に書かせたりすると,長針は文字板の6のところをさしているか,短針は文字板の8をさしていることがある。「午後1時から午後5時までの時間はどれだけか。」と問うと,「5時間」と誤って答えたりすることがある。
このような場合には,実物のとけいを用いて針を動かしていくと,これが誤解であることは,やさしくわかるのである。これなしに指導を進めていくと,こどもは,だんだんにわからなくなり,理解をもって学習を進めていくことができなくなる。
もう一つの例をあげてみよう。順序数の指導をするのに,石を10個ずつ横に10列に並べて,「36番目は」と問うたとする。こどもは,まず10個ずつ3列まで数え,次の4列目を数えないで3列目の6番をさして,36番目と答えることがある。このようなときには,はじめから1個ずつ数えさせてみると,初めの誤解を容易に気付かせることができるであろう。また,10個ずつ並んでいる右端までで10であることを確認して,10,20,30と数えて,4列目の6番目をさせばよいことに導くことも考えられる。とにかく,このように,こどもが誤ったときには,すぐに正しい結果を教えないで,その結果を確かめるように導き,誤った結果が出てきた原因をつきとめて,理解をもたせるようにすることを忘れてはならない。
もう一つの例をあげてみよう。2年生のこどもたちに三位数の記数法をテストしてみると,125を1025,407を470などと書き誤るこどもがある。このような場合に,観念的にことばだけで位取りを教えると,そのときは理解したようにみえても,後になって,再び同じ誤りをくり返すことがある。これは具体的な事実をとおして理解していないから,教えられたことが身についていないためである。この場合に,運動場に出て,石拾いなどさせ,拾い集めた石を100個ずつのグループ,10個ずつのグループ,残りというように並べさせ,各位の数字は,各グループがそれぞれいくつあるかを表わしたものであることを説明すると,各位の数字,特に空位の意味を正確に,こどもが理解するものである。また,低学年のこどもは,「よしおさんとただしさんは合わせて150円持っています。そのうち,ただしさんは50円です。よしおさんはいくらですか。」と問われると,200円と答えることがある。これは「合わせて」ということばがある時は,いつでもよせればよいと誤解しているからである。このようなときにも,具体的なおかねを示して,これを説明して理解をもたせるようにすることを忘れてはならない。このように絶えずこどものまちがいや誤解がどこにあるかを,テストや指導の途中における観察によって発見し,それを具体的な事実に結びつけて説明してやることが,理解をもたせるために,たいせつなことである。
以上は理解をもって学習していくための指導の方法について述べたのである。数量関係や演算が実際の生活の場において,じゅうぶんに使いこなせるようになるためには,特に,それらのことがらが日常生活の場としっかりと結びついていなければならない。しかも,これをとおして,算数のよさが明らかにされてくるのである。したがって,具体的な教材や,日常の生活経験と結びつけて指導することの意味は,数量そのものを単にわかりやすく理解させるための手段としてだけ重要だというのではない。これをとおして,日常生活と結びつけることができ,このよさを明らかにするために必要だからである。なお,こどもは,ことばだけをなかだちにしたのでは,よく誤解を起すものである。このことばの抽象性を補って,抽象されたことばの真の意味を体験し,正しい理解をもって学習していくようにするためにも,具体的な教材,教具は重要な意味を持っているものである。
5.日常生活を改善しようとしての学習
| どのように指導したら,こどもが学習したことを使って,日常生活を改善することができるようになるか。 |
従来の算数の指導において,計算はできるが,事実問題やいろいろの問題などの,いわゆる書かれた問題が解けないと言われたり,また,こどもが計算などの技能を日常生活に使わないですませていると言われる。一般に技能は,うまく使うことができて,はじめて意味をもつものである。そのためには,巧みに使いこなして,これを日常生活の改善に役だてることのできるように指導しなければならないが,技能をうまく使いこなせるようにするには,技能が実際生活のどんな場で,どのように使われているかについて,じゅうぶんな理解をもっていることが最もたいせつである。たとえば,とけいの文字はよく読むことができる。しかし,とけいが正しい時刻をさしていないと,社会の人々とうまく協力していくことのできないことは,わかっていないことがある。ここで主張しようとしているのは,とけいから時刻を読みとることもたいせつであるが,それが社会でどんなはたらきを持っているかを正しく理解し,とけいをうまく使って社会生活を楽しくしたり,規則正しく生活をしたり,余暇をうまく使ったりすることのできることも,たいせつであるということである。
ここでは,学習したことをうまく使って,めいめいが生活を改善することができるようにするために,どんなところに目をつけたらよいかを考え,ここに,その主要なものを取り上げて説明することにする。
(1) 数を用いた経験をほめてやる
こどもは,家庭にいるときや,算数以外の学習のときに,うまく算数を用いることがある。このような経験を持っているこどもがいたら,みんなの前で,その話をしてもらい,そのことをほめることが,最も重要なことの一つである。たとえば,こどもが休暇中に,生活を規則正しくしようとして,とけいを使い,自分の生活の計画をたてたとする、また,親類の家から,秋祭りに来るようにとの手紙をもらってから,どんな時刻にどんな乗物を使ったらよいかを調べたことがあるとする。このように,こどもは学校外の生活でも,また算数以外の学習のときにでも,算数を用いることがあるものである。このようなこどもの生活において,知らず知らずのうちに算数をうまく使っていることがあったら,これこそ,算数がこどもの身についたといえるのであって,算数についての指導の窮極のねらいを達成しているともいえる。このような場合には,どんな事がらについて,どんなに算数を用いたかを,そのこどもに話してもらい,惜しみなくほめることがたいせつである。また,実際に意義のあることである。これは算数を用いたときだけに限らず,どの教科についてもいえることであろう。教師がこどもの行動を,常にこのような観点から観察して,うまく使ったことを発見しては,それをクラスの人たちに紹介することを忘れてはならない。これと同時にたいせつなことは,もっとうまい解決をするための目のつけどころがあったら,これについて示唆を与えていくことを忘れてはならない。
(2) こどもの直接している事がらを取り上げて指導する
こどもが日常生活において,自分の思考や行為を改善するようにするためには,問題を解決する能力を伸ばすようにくふうしなければならない。この能力を伸ばしていくのに最も必要なことは,こどもの当面している直接的な問題を取り上げることである。こどもは日常生活で,いろいろな困難に当面して困惑していることがある。じゃんけんでおはじき取りをして遊んでいるうちに,取った数を記録しておかなかったために,勝負けについて,いざこざを起すことがある。また,学級費や給食費などを集めるときに,小銭で持ってくる人があって,いちいち数えて確かめたり,反対に大きなおかねで持ってくる人があって,おつりを出したりなど手数がかかって,そのために誤りを起して困ることがある。また,月々に一定の金額だけのおこづかいをもらっていて,その使いみちを記録しておかないために,使いみちを両親から聞かれて困ったり,もっとうまく使おうとくふうしようとしても,使いみちがわからないで困ることがある。
このように,こどもが実際に困っている事がらを取り上げ,問題を見いだして,これを解決しようとして指導すると,ひいては,こどもが自分の当面している困難を解決していくようになるであろう。このような意味から,こどもの当面している困難をきっかけとして指導していくと,やがては,こどもの思考や行為を改善していくように仕向けることができると考えられるからである。
このような取り上げ方は,こどもが自分の問題として持っているものを解決しようとするのであるから,学習に対する意欲もあり,自主的な学習もできるようになる。このために,こどもは算数のよさを理解するだろうし,また,こども自身の生活の進歩にどんなに役だっているかもよく評価できるわけである。
上に述べたことを,次の具体的な例について説明しよう。
こどもたちが遅刻して楽しい映画会に参加できなかったとか,友だちと,朝8時のバスで遠足する計画をたてたが,ひとりが遅刻したためにバスに乗り遅れて,全体の人が不愉快になったことなどの話し合いから,「きめられた時刻に,みんながきっちり集まることができるようになるには,どのようにしたらよいか。」を問題に取り上げ 学習することにしたとしよう。
こどもは,とけいの読み方や道のりを時間ではかったりする方法をくふうしたりして,この問題の解決を考えるであろう。この問題の解決によって,とけいが日常の生活で相互に協力して楽しい生活をするのになくてならないものであることや,とけいが正しい時刻を示すように時報に合わせておかなければ役にたたないことなどを,はっきり理解するであろう。
これに比べて,単にとけいの文字板を見て,とけいを読みとるだけに指導の重点を置いた学習では,思考や行為の改善に役だつことを明らかにすることができないであろう。
要するに,前者のように,こどもの直接している問題を取り上げ,問題解決の力が伸びるように指導していけば,こどもは,とけいがその問題解決に役だっていることをよく理解するであろう。また,どんな生活の場で,とけいをどのように使うことができるかも知るであろう。また,このように指導していけば,教師は,とけいに対する具体的なこどもの行為によって,学習の成果をはっきり評価していくこともできるのである。
(3) こどもの当面する問題と似かよったものを取り上げる
こどもが直接に当面している問題は,指導の上にどんなに役だてることのできるものであるかについては,さきに述べたところである。
しかし,そのような問題だけで算数を日常生活に生かして用いることができるまでに,指導することのできないことがある。このような場合には,日常生活に起る問題とできるだけ似かよった問題を選ぶようにするのがよいことはいうまでもない。
(4) 反復練習して,いつもやさしく使えるようにする
今までに述べたことは,主として,学習したことが日常生活にうまく使えるようにするためには,どんなに技能と生活の場とを結びつけたらよいかについて述べたものである。しかし,日常生活に生かして用いることができるようにするためには,これだけでは,ふじゅうぶんである。技能と生活の場を一応結びつけることができたとしても,必要に応じて,これを気楽にしかも的確に使えるようにすることを忘れてはならない。
このようになるためには,反復練習の必要であることはいうまでもない。さて,その反復練習するための目あてとなるものを,二つの類型に分けて考えることができる。その一つは演算の意味などを拡充し,一般化するためのものである。他の一つは,技能をすっかり身につけて,必要に応じて,これを気楽に用いることができるようにするためのものである。この二つの類型は,それぞれどんな内容を持っているかを明らかにするために,具体的に説明してみよう。
前者は,どんな時に,よせ算で解決することができるかとか,ひき算で解決することができるかとか,また,かけ算でよいとか,わり算でよいとかが,気楽に判断できるようにすることなどをねらっている。このねらいを達成するためには,演算の意味などがよく理解できたところで,それを適用できるいろいろな身近な事例を用意して,これを練習させ,その意味を拡充し,一般化して,その内容を豊かにすることがたいせつである。
たとえば,さきにあげたとけいについての指導において,次のような練習をさせるのである,家から学校まで25分必要であるとして,このこどもが,8時10分の始業に間に合うようにするためには,何時に家を出ることにしたらよいかを考える,また,学校から帰って家の手伝いをする計画を立てるとか,楽しみ会をする際のプログラムを組むときに時間が延びて遅れないように計画を立てることを考える。このように,時刻や時間についての計算を適用する場をできるだけひろく,できるだけ数多く用意して,適用練習をする機会を多くすることが,第一の類型について主張しているところである。
後者は,技能についての理解が成立して,その技能のもとになっている原理が理解されても,その適用が簡単なときにはうまくできるが,適用する手続が複雑になると,うまくできないのが普通である。
たとえば,分数についてのよせ算の原理といっても,整数,小数あるいは時間の時と同じであって,いわば,位取りをそろえることである。しかし,この原理がわかりさえすれば,分数についてよせ算であれば,どれでもよくできるとは考えられない。
そこで,分数の計算の手続の簡単なものから複雑なものに,いくつかに分類して,それらについて,どの段階でも正しく計算できるように,じゅうぶん練習する時間と機会を与えなければならない。これが第二の類型として主張しているところである。
この際,じゅうぶん注意してほしいことは,ここでいう練習は,時間的に早く,しかも,機械的にできるようにするための反復練習だけをさしているのではない。理解された原理や概念などを,いっそう確実に,しかも,正しく身につけさせるためのものである。
(5) 問題の解決の手がかりをこどもが見いだすようにする
こどもが,算数を日常生活に用いていくことができるようにするためには,こどもが,みずから算数を用いて問題を解決していくようにしなければならない。その手はじめとして,こどもが,みずから問題解決の手がかりを見いだすことができるようにしなくてはならない。
このための有効な方法の一つは,生活の場,いわば問題の場を豊富に持っていて,自分の現在当面している問題の場と,今までに学習して持っているものとの類似点を見いだすことができ,そこから手がかりを得るように指導することであろう。
他の一つの有効な方法として,こどもに対する発問についてくふうすることである。いわば,教師の援助や示唆が必要であったとしても,教師はその必要な限度を,こどもの行動から鋭敏に見きわめて,こども自身がみっちり考えていく部面をできるだけ多くするように,発問をくふうするのである。ところが実際の指導においては,教師がややもすると,この手がかりをあらかじめ考えておくのはよいとして,これを一問一答の形式にまで分解していき,こどもが腰を落着けて考えていくのを妨げているとさえ見えることがある。教師は,こどもが,独力で解快していくことのできる限度をじゅうぶんに知り,解決の手がかりを必要とする場合でも,こどもの考える力や創造力をそがないように指導したり助言したりするために,どの程度までのことは発問して,手がかりを与えたらよいかについて,綿密な案を持つことがたいせつである。しかも,指導の実際にあたっては,こどもの発する声や動作,こどもの質問などの具体的な行動をとおして,個々のこどもの必要な限度を察知し続けて,指導を進めることが必要である。
要するに,教師の発問は,できるだけ少なくして,こども自身が考え,できるだけ多くのことを自分で見いだすようにくふうすることが肝要である。ここに述べたことを,具体的な例について脱明してみよう。
買い物ごっこのときに,「どのようにおかねを出したら,見て金高がすぐわかるようになるだろう。」ということが問題になったとする。これは,さきにも出した例であるが,こどもが当面している困難をはっきり自覚しておりさえすれば,その解決の目やすは持っているわけである。
(a) 同じ金高のお札はまとめておく。
(b) 枚数ができるだけ少なくてすむようにする。
このようなことは,問題を取り上げたときに,もう見当がついているはずである。
教師は次のような発問をする。
○どんなおかねの出し方がよいでしょう、38円のコンパスを買ったとして,机の上に並べてみましょう。
おかねの並べ方に,次のような並べ方が予想されるので,机の上にならべているようすを観察する
| (ⅰ) |
{ |
10円札 3枚
5円札 1枚
1円札 3枚 |
(ⅱ) |
{ |
10円札 3枚
1円札 8枚 |
(ⅲ) |
1円札で38枚 |
だれも(ⅰ)のような出し方をしたら,その出し方を一般化するように,85円で,飛行機の組立材料を買ったときなどの出し方を考えさせる。これもできたら,今までの出し方をまとめるために,次のような発問をする。
○この出し方は,どんなわけでよいのですか
さらに,次のような発問へ発展していく。
○ねだん表を見て,出すお札をどのようにしてきめたらよいですか。今までのおかねについて,考えをまとめましょう
このようにして,43円などと書かれた数字を見て,10の位の数字は10円札の枚数,1の位の数字は1円札の枚数を表わすとみてよいことをおさらいするとともに,位取りの原理とおかねの出し方とを結びつけるようにするのである。
ときに,(ⅰ),(ⅱ),(ⅲ)の出し方のまじっていることがある。このような場合には,(ⅱ),(ⅲ)の出し方を示したこどもに,(ⅰ)の出し方と比べさせて,どちらがよいか,またそのわけはどうかなどと発問して考えさせていく。
とにかく,必要に応じて,こどもの行為や思考を方向づけていくように示唆するがよい。そして,こどもに,できるだけのことを考えさせ,最少限の発問で,こどもの学習の方向づけをすることがたいせつである。
(6) 指導の機会を見のがさない
算数を用いる場合は,算数について指導しているときだけではない。算数についての指導を主として考えているとき以外の場合にも,多いのである,したがって,算数を主要な指導のねらいとしていないときにも,必要に応じて算数について指導してこそ,はじめて日常生活に算数を用いるように指導することができるのである。言い換えると,算数を使う機会があったら,それがどんな場合であっても必要に応じてそこで時間をとり,算数が有用であることに,こどもの目を向けるようにしなければならない。
たとえば,夏期になって伝染病が流行し,「どのようにしたら伝染病になる人を少なくすることができるか。」を問題にして,主要なねらいを理科の目標においたとしよう。そして,上水道,下水道の設備をよくすることが,赤痢やチフスを少なくするために役だちそうだと考えたとする。上下水道の設置される以前とその後の罹病の様子を比べようとして,罹病の割合を計算したとする。このために,すでに学習した百分率を使うことになったとする。ここで,百分率の便利さや有用なことを取り上げて,確認させるようにすることがよい。
教師がこのようなことに対して注意を払えば,こどもは学んだ喜びをしみじみと味わうことになり,さらにうまく使おうとする意欲を起すことであろう。
これがひいては,こどもが算数を日常生活に用いていく傾向を伸ばしていくのに,役だつものとなるのである。
以上は,こどもが算数を日常生活に用いていくようにするためには,どのようにしたらよいかを考え,これを述べてきた。これらは,一つのことをいろいろな角度から述べたにすぎない。決して,全く違ったことを述べているのではないことを注意しておきたい。
6.こどもと学習内容
| 学習内容を,ひとりびとりのこどもに適合させるには,どのように指導計画をたてたり,指導したらよいか。 |
(1) 標準テストなどで,こどもの進度を知る
学習内容が,ひとりびとりのこどもにじゅうぶん理解され,こどもの身につくようにするためには,その内容を累積的,漸進的に指導することが必要である。新しい理解は,今までの理解と関係なしに生れてくるものではなく,必ず,今までの学習の上に積み上げられて,生れてくるものである。
学年の初めに,その学年の指導内容を決定するにあたって,こどもは,前学年までにおいて,どんなことを学習したか,また,それによって,どんなことを理解しているかを知ることは,教師にとってたいせつなことである。
これを評価するには,標準化されたアチーブメントテストでなくても,こどもの進度を知るために教師が作ったテストでじゅうぶんである。とにかく,評価の方法として,必要に応じていろいろな方法がくふうできるであろう。その方法については,次の章の評価のところを参照していただきたい。このようにして,評価ができると,そのこどもの今学年の学習を,どこからはじめたらよいかが明らかになってくる。
さて,こどもの進度を知るための評価として,次の二つのことがらをあげることができる。
その一つは,前学年の指導内容としてあげてあるものでなくても,算数の学習において基礎的な事がらとみられるものについて調査することである。たとえば,高学年のこどもであっても,どのこどもも乗法九々を正しく記憶しているとはいえない。また,乗法は,どんな場合に使ったらよいかなどについても,よく知っているとはいえない。このようなことについて評価をしてみるのである。
他の一つは,今学年の指導に支障をきたすおそれのある事がらについて,評価をしてみることである。たとえば,5年生で時間についての加法や減法を指導しようとする。この場合に,時間についての加法や減法の基礎的な事がらと考えられるものは,時刻と時間の区別,1時間は60分であること,午前と午後との関係などであるが,これらがじゅうぶんに理解されているかどうかを評価してみることが,まず,必要である。
このように,学年の初めに,前学年の指導内容と直接には関係のない基礎的なものと,前学年の指導内容の中て理解されていないと,今学年の指導にさしつかえる事がらについて,こどもの程度を明らかにすることがたいせつである。
このようにして,こどもの程度が明らかになったら,それを参考にして,今学年の指導計画を修正し,その指導内容がこどもの能力に相応するように指導していくことが必要である。
(2) 能力差を考慮に入れた指導計画をたてる
新しい理解は,常に今までの学習を土台にして,その上に段階的に積み上げられていくものである。このような意味から,ひとりびとりのこどもの能力や理解の程度を基礎にして,その上に学習を進めていくことによって,こどもは,次の理解がいっそう容易にできるようになるのである。
そこで,二位数に基数をかける計算を指導しようとする場合を例にとって,考えてみよう。こどもが今までに習得している,かけ算についての理解や能力には,こどもによって多少違いのあることはいうまでもない。
○乗法九々が正しく速く唱えられ,また,それが事実問題に適用できる。
○16+16+16は,16×3として計算すればよいことがわかっている。
○3×2は,2×3に等しいことがわかっている。
○0×nは,0に等しいことがわかっている。
○231の2は,100が2個,3は10が3個,1は1が1個ということを示していることがわかっている。
○加法での,繰上がりについての正しい理解をもっている。
これらのいくつかの事がらについては,正しく理解され,正しく処理できるが,しかし,他のいくつかの事がらについては,まだ,ふじゅうぶんなこどもがある。とにかく,単なる二位数に基数をかける計算を指導するような,簡単だと思われる場合においても,その基礎となる理解や能力のもち方は,こどもによって多種多様であるといえる。
このように,能力差のあるこどもに対して,一様に同じ程度の内容を指導すると,多くのこどもは,わからないままに終ってしまうか,さもなければ,わかりきったことを何回も聞いて,退屈してしまうかの,どちらかであるといってよい。 このようなことを避けるためには,できるだけ,こどもの能力差に応じて,どのこどもも,自分の必要とする学習ができるように,指導計画をたてる必要がある。
(3) こどもの当面している困難や混乱を見定める
こどもの書いたものや,口頭で説明している内容を詳しく研究し評価してみると,そのこどもの当面している困難を見定めたり,また,こどもが混乱を起している内容を発見したりすることができるものである。
この努力をしないで,どんなりっぱな指導計画をたてても,また,どんなにりっぱに指導をしているように見えても,それは形式的な指導計画であり,指導であるといわねばならない。
たとえば,郵便はがきのねだんの変化をグラフに表わさせてみると,こどもの中には2銭も2円も同じように,2円のところにしるしをつけて,平気でいることがある。また,こどもの中には,2円のところはわかるが,2銭は,どんなに表わしたらよいかがわからないで,まごまごしているこどももでてくる。この場合に単位がみな円であればできるのであるが,銭という単位がはいってきたために困難になり,混乱を起していると考えられる。
このように,こどもが,困難や混乱に当面しているような場合には,その状態をできるだけ早く発見し,こどもが自分で,その障害を取り除くことができるように,適当な手がかりを与えて,次の学習に進むことができるように,指導することがたいせつである。
もちろん,こどもが困難や混乱に当面しているときに,直ちに,それを救うつもりで,簡単に解答を与えてしまうようなことは,避けなければならない。もし,そのような指導を繰返していくと,自分の力で,自分の問題を解決しようとする意欲や能力を伸ばすことができないばかりでなく,何事にも,人の力を借りなければできないこどもにしてしまうおそれがあるからである。
したがって,一見親切にみえるこのような指導は,実は,こどもに対して,不親切極まる指導であるということができる。
こどもが当面している困難や混乱が,どんなものであるかを,こどもにも気づかせるようにしたり,どのようにしたら,その障害を克服できるかを,そのこども自身でもくふうするように指導することは,きわめてたいせつなことであるといえる。
以上述べたように,こどもの当面している困難や混乱を見定めることは,指導内容を,ひとりびとりのこどもに適合するように,計画を修正していく上に,必要欠くことのできないことである。
(4) 遅れているこどもの困難をつきとめる方法
前にも述べたように,指導内容が,こどもに適合するようにするためには,こどもの書いたものや説明の中から,こどもの書いたものや説明の中から,そのこどもの困難や混乱を見定めるようにすることが必要である。その場合に,教師にとって最も困難なことは,進度の遅れているこどもの困難や混乱が,どこにあるかをつきとめることである。それは遅れているこどもは,一般に,発表することをいやがるからである。たとえ,わかっている場合であっても,人前で発表することをいやがるのが遅れているこどもであるといえる。したがって,遅れているこどもの困難や混乱がどこにあるかを見定めることは,きわめてむずかしいことであるといえる。
遅れているこどもに,その混乱している点を見いださせるには,正しいものと比べさせる方法が考えられる。たとえば,計算の仕方に誤りのあることがわかったら,正しい計算のしかたと比べさせ,どこに誤りがあるかを見いださせるようにするとよい。こどもは,これによって,自分はどこに誤りがあったかを,はっきりつかむことができるのである。これができたら,次に,どうして,正しいしかたのようにしなければならないかを考えさせていくと,なおいっそう自分の誤りを明らかにすることができ,正しいしかたを身につけることができるのである。なお,このような指導をしているときに,自分の誤りを指摘することができたら,教師は,ほめることを惜しんではならない。こどもは,教師にこごとをいわれるよりも,ほめられると,学習に興味をもち,学習に対する意欲をもつようになるからである。
このように,遅れているこどもを伸ばすには,そのこどもと教師とが協力して,困難や混乱をつきとめ,教師はその内容が,そのこどもに適合するようにくふうして指導計画をたて,実際の指導にあたることがたいせつである。
このように,遅れているこどもを伸ばすには,そのこどもと教師とが協力して困難や混乱をつきとめることがたいせつである。困難や混乱をつきとめることができると,それをもとにして指導計画をたてることができ,実際の指導も,こどもに適合するようにすることができるといえる。したがって,こどもの困難や混乱をつきとめることは,指導上きわめて重要なことであるといえる。
(5) 必要があったら,たった,ひとりのこどもであっても,その必要に応ずるように指導する
学習指導でたいせつなことは,めいめいの能力に応じて,学習していけるようにすることである。したがって,進んだこどもは,その能力に応じた,むずかしいことについて学習するし,遅れているこどもは,その能力に応じて,最大限の仕事をするように,指導することがたいせつである。
ひとりの教師が,多くのこどもを受け持って指導していることから,とかく,同じ内容を,いっせいに指導しがちである。このような指導をすると,必ず学習に参加しないで遊ぶこどもがでてくる。この遊ぶこどもというのは,特に遅れているこどもはいうまでもなく,ずっと進んでいるこどものことでもあるといえる。
計算の意味のわからないこどもが,級でわずかひとりであるからといって,そのこどもの指導をなおざりにすることはできない。そのようなこどもに対しては,おはじきや石ころなどのような具体物や半具体物を使って,そのこどもが理解できるまで,教師は努力すべきである。また,ずっと進んだこどもがいるような場合に,そのこどもが,今指導している内容では簡単すぎたり,あきるようなことが起ったら,もっと進んだ事がらについて学習させるようにすることを忘れてはならない。
教師は座席表のような記録用紙を用意しておき,こどもがどこに困難を感じているか,また,どんな問題や学習活動が,こどもにぴったりしているかなどを見定め,こどもごとに記録しておくようにするとよい。
この記録をうまく使うと,そのこどもは,どんなところに混乱を起しているかがよくわかり,こどもの必要に応ずる指導が容易になる。
したがって,特別に指導を要するこどもが,ただのひとりであろうと,このように指導法をくふうして,指導にあたることはたいせつなことである。
遅れているこどもを指導する場合に,特に注意しなければならないことは,遅れているこどもを指導するために,他のこどもを遊ばせないように,計画したり,指導したりするということである。したがって,他のこどもが熱心に学習をしているときに,これらの遅れているこどもの指導もうまくできるように,くふうすることが必要であるといえる。
このように,学習指導は,一般のこどもの指導とともに,特別指導を要するこどもがたとえひとりであっても,そのひとりに対しての指導も行き届くようにくふうされなければならない。このようにされてはじめて,指導内容が,ひとりびとりのこどもに適合するようになったといえるのである。
(6) 問題のありかや,困難を克服する方法を,こどもにわからせる
学習の過程で,こどもがつまずいているときに,そのこどもが,障害を自分で見いだすように指導することの必要であることは,すでに述べたところである。それと同時にその障害をなくすためには,どんな方法があるか,また,どんなことをしなければならないかを,こども自身が納得するように指導することも必要である。
たとえば,二位数に基数をかける計算で,それができないでいるときに,その原因が乗法九々の記憶違いにあることがわかったら,その誤っている九々を,カードに書き,そのカードで,くり返し練習するように,助言するのは,その方法をわからせる一例である。
このように,こどもの当面している困難や混乱からみて,基礎になる事がらをもう一度練習しなおしてみる必要が起る場合もあろう。また,教科書その他の参考書について,解決の手がかりを求めることもあろう。とにかく,このような場合に,こどもが,その困難をできるだけ自分の力で解決できるように,その方法に対して適当な助言を与えることが必要である。
こどもの中に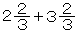 の計算ができないものがあった場合に,こどもに,分数の加法を小数の2.7+3.5のような計算と比べて,どんなところが同じで,どんなところが違っているかを研究させるのである。このようにすると,その違っているところに注意を集中していき,この困難をとり除くことがある。
の計算ができないものがあった場合に,こどもに,分数の加法を小数の2.7+3.5のような計算と比べて,どんなところが同じで,どんなところが違っているかを研究させるのである。このようにすると,その違っているところに注意を集中していき,この困難をとり除くことがある。
このように,こども自身が困難な問題のありかを見いだし,さらに,解決の方法を考え出すように指導していくと,指導内容は,教師が考えて与えたものでなくなり,こどもひとりびとりが,自分自身で考え出したとみられるものになるのである。このような考え方で指導したならば,指導内容が,ひとりびとりのこどもに適合することはいうまでもなく,学習がこどもによって,積極的に進められるようになり,教師は,それによって節約された労力を,他の有効な直接指導のために用いることができるようになるのである。
以上は,学習指導の計画や実際が,こどもひとりびとりにぴったり適合するようにくふうされることが,ひとりびとりのこどもを伸ばし続けていくために,きわめて重要であるということを述べたのである。
7.有効な反復練習
| どのように,実際に適用することや,練習,反復練習を指導したら,算数を有効に用いることができるようになるか。 |
算数を有効に用いることができるように,実際に適用してみることや,練習あるいは反復練習を指導するには,どんなことに注意したらよいかを述べてみようと思う。
(1) こどもが,算数を実際に使ええるようになってから,反復練習にとりかかる
特に,計算についていえることであるかもしれないが,導入的な指導をしただけで,すぐに,その計算の反復練習をさせるような指導が,よく行われているようである。
この方法は,必ずしも学習の効果をあげるものであるとはいえない。
たとえば,そろばんの運珠法を,ひととおり指導したところで,すぐに反復練習に移ることは,その反復練習の価値を高めることにはならない。反復練習の前に,そろばんは,どんなときに使うと有効であるか,どんな場合にそろばんで計算するより筆算でするほうが便利であるかなどについて,じゅうぶんな指導がなくてはならない。このような指導をしたあとで,練習に移ることがたいせつである。このようにしないと,その技能を,日常生活にうまく生かして使うことができないからである。
こどもの中には,ノートに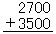 とわざわざ筆算形式に書き改め,それにそろばんをあてて計算し,その結果をその下に書いているものがある。これは,そろばんを,どんな場合に使ったらよいかについて,じゅうぶんな理解をもっていないからである。
とわざわざ筆算形式に書き改め,それにそろばんをあてて計算し,その結果をその下に書いているものがある。これは,そろばんを,どんな場合に使ったらよいかについて,じゅうぶんな理解をもっていないからである。
このように,こどもが技能の持つ社会的な意味について,じゅうぶんな理解をもち,その技能を使う準備がじゅうぶんにできたところで,反復練習にはいるようにしなくてはならない。このような点に注意して反復練習を指導するならば,こどもは,その技能を有効に用いることができるようになるであろう。
(2) 技能が,その学習の場において,有用なものでることを明らかにする
こどもが学習に興味をもったり,また,切実な必要を感じたりするようにするためには,これから学習しようとする技能や,あるいは現在学習しつつある技能が,こどもの当面している問題を解決するのに非常に有効なはたらきをもつものであることを,明らかにすることが必要である。その技能が,単に,こどもの当面している問題を解決するのに役だつばかりでなく,他のいろいろな問題を解決するのにも,きわめて大きな役割を果たしていることもまた,明らかにされなければならない。このようにすれば,技能を練習し,それを身につけようとするこどもの意欲は,さらに積極的になるであろう。また,こどもはその技能を身につけようとして,学習に対する努力も惜しまなくなるであろう。
夏休みに,こづかい帳を記録しておいて,それを二学期の初めに整理しようということにしたとする。筆算で支出の合計を求めようとすると,非常に多くの数を加えなければならないので,めんどうである。そこで,その計算をうまくするしかたはないだろうかと,こどもに考えさせると,こどもの中には「おかあさんは,いつも家計簿の整理をするとき,そろばんを使っていらっしゃる。ぼくたちも,そろばんで計算してみよう。」という者がでてくるであろう。そこでそろばんでやろうとすると,そのしかたがよくわからない。しかし,そろばんは,こづかい帳ばかりでなく,学級費や給食費の合計を整理する場合など,その使われる機会が非常に多いことが理解されると,こどもは,いっそうそろばんの有効なことを知り,その技能を身につけようとして,積極的に学習するようになるであろう。このように,これから学習しようとする技能が,その学習の場で有効なことがわかり,さらにその上に,その学習の場だけでなく,他の学習の場においても,問題を解決するのに有効であることが明らかにされ,その上に反復練習が積まれると,こどもは,その練習された技能を,有効なものとして使えるようになるのである。
(3) 計算などについて,理解をもたせる
「一冊5円のノートを,6冊買ったら,いくら支払えばよいでしょう。」という問題を解くときには,「5円×6」として,その結果を求めるのが普通である。ところが,この問題を,「ノートを6冊買いました。どれも1冊5円でした。ぜんぶでいくら支払ったらよいでしょう。」とすると,「6×5=30(円)」として結果を求めるこどもがでてくるであろう。
こどもが,このような誤った解決をするのは,かけ算の意味をひととおり理解しているにしても,その理解が形式的になっていることを示しているといえる。
問題が,どんな形式で出されようとも また,いくつかの条件がどんな順序で書いてあろうとも,かけ算を式で示すとすれば,(グループの大きさ)×(グループの個数)=(量全体の大きさ)であることが,こどもにじゅうぶん理解されておらなければならない。この一般化がふじゅうぶんなために,6×5=30(円)というような式を書くのである。
とにかく,形式的な練習に移るにさきだって,技能などについての理解をじゅうぶんに伸ばすことを忘れたのでは,反復練習したものを有効に用いることができないであろう。
(4) 計算などの手続が,正しくできるかどうかを確かめる
計算などの手続は,これについての正しい理解のうらづけがあって,はじめて,正しくできるものである。ところが往々にして正しい理解をもたないために,誤った手続を用いることがある。それにもかかわらず,反復練習の指導に進んだとすると,こどもが,その誤った手続をくり返していくうちにそれを,はっきりと身につけてしまう。これをあとになって気がつき,この悪いくせを改めようとしても,なかなか思うように改まらないものである。もしも,誤って記憶していたり,理解がふじゅうぶんであったら,できるだけ早く,これを正しくするための指導にとりかかることが必要である。
たとえば,乗法九々で,「八,六,四十二」「六,八,四十二」などと,まちがって記憶しているこどもがある。このような誤りを,何回もくり返していたのでは,実際の問題に,九々を用いて正しく解決することができないし,また,学年が進んだときに,大きい数についての乗法や除法も正しくできないであろう。高学年の乗法や除法の誤答を調べてみると,その原因が,乗法九々の誤りにあることの意外に多いことに気づくであろう。したがって,このような基礎的な事がらについて,こどもが正しくできるかどうかを,よく確かめておくことは,きわめて重要なことであるといえる。
こどもが正しく理解しているかどうか,また,正しい手続で計算しているかどうかを確かめるには,こどもに,口頭で発表させるのもよいし,また,ノートなどに書かせて調べてみることもよい。また,そろばんのように,実際にそろばんで計算させてみて,その運珠が正しいかどうかを確かめなければならない場合もあるだろう。とにかく,教師は,こどもが算数を正しく使うことができるかどうかを確認して,はじめて練習に進むようにすれば,その練習が,こどもにとって,いっそう有効なものとして使われるようになるであろう。
(5) 成功による満足感を味わわせる
こどもが,学習に興味をもつようにするには,その一つとして,自分はこれだけのことができたという喜びを,感ずるようにしてやるということをあげることができる。こどもが学習に成功し,それによって,満足感を味わうと,次の学習に対する意欲も高まり,学習が積極的に始められるものである。
学習において,成功の喜びを味わえるようにするためには,こどもの学習する内容が,ひとりびとりの能力に即し,しかも必要に応じたものでなくてはならない。たとえば,低学年のこどもにとって,輪投げ遊びなどは興味のあるものである。もし,こどもが,輪投げをしようということになると,お互に,はいった輪の数を調べる必要が生れてくるであろう。そこで,数えるという必要が生れてくる。また,大ぜいで交互に輪投げをする場合には,はいった輪の数を忘れないようにするために,その数を記録しておくと便利だということになろう。そこで表を作って,それに数を記入することが考えられ,ここに記録するという必要が生れてくるのである。
このように,こどもが,必要と興味に応じて学習していくと,学習は積極的になり,その学習をする喜びにひたることができるであろう。学習がこのようであれば,こどもが学習に成功することはまちがいないことであろう。このようにすれば,今まで数えることのできなかったこどもでも,数えることができるようになるであろう。また,数字を書くことのできなかったこどもも,遊びのうちに,数字が書けるようになるであろう。
こどもの能力や必要に応じて学習をし,その必要を強く感じているときに反復練習をすると,その反復練習が,当面する問題の解決に役だつし,しかも,それによって,こどもは,成功の満足感を得ることができるであろう。このようにしていけば,こどもは,反復練習をしたことを身につけ,これをうまく生かして使うことができるようになるのである。
(6) 反復練習したことを,実際に応用するようにする
反復練習したことが,多くの学習の場で使われると,その技能が,ますます確実なものとなるのである。そのためには,反復練習すると,たしかにこども自身のためになり,それによって,次の学習が大いに気楽にできたという感じをもたせるようにして,こどもが進んで,練習をくり返すようにしてやることが必要である。
例をものさしの使い方にとって,これを説明してみよう。
まず,ものさしの使い方や目盛の読み方について,一応の指導ができているとする。あとで,こどもがお店やさんごっこをするために,たくさんのお札を紙で作ることになった場合に,かってな大きさで作ると,大小さまざまなお札ができ,お札のやりとりや整理に不便である。お札の寸法をそろえると取扱に便利であることがわかると,こどもは,ものさしを使って,きちんと寸法をはかり,同じ大きさのお札を作るようになるであろう。前に学習したものさしの使い方や耳もりの読み方を活用すると,新しい学習がいっそう気楽に,能率的に,しかも正確に進めることができるのである。そこで,こどもは,ものさしを使うと,どんな便利なことがあるか,また,ものさしを使うと,どんなに仕事が気楽にできるかなどに気づくであろう。このように指導していけば,こどもは,ものさしの使い方を喜んで練習するだろうし,また,その反復練習したことを,有効に用いることができるようになるだろう。
反復練習を,単に,技能をくり返し練習するというだけにとどめておいては,なんの意味もないことになる。練習された技能が,どしどし,実際の場に使われるようになり,それを使うことのおもしろさがわかるようにしなければならない。このような指導をとおして,はじめて,こどもが,反復練習したことを,いっそう有効に使うようになるのである。
(7) 練習の機会を,できるだけ多くつくってやる
一つの技能が,こどもにじゅうぶん使いこなせるようになるためには,単に,反復練習をするだけでは,じゅうぶんであるとはいえない。それにさきだって理解したり,実際に適用してみたり,また,考えながら練習したりして,こどもが自信をもって,学習し続けるようにすることが必要である。
さて,反復練習は,単に,機械的に使えさえすればよいと考えて,形式的にまとめて練習することをさしているのではない。その技能を,気楽に使えるようにするために,こどもが何回も経験できるような,実際の場を設けて,指導することをねらっているのである。たとえば,ものさしで紙の長さをはかることを学習したら,さらに発展して,身のまわりにある,いろいろな物の長さをはかってみるように指導するのである。いわば,ものさしを使うことを必要とする環境をできるだけ多くつくり,その練習をとおして,ものさしの使い方を確実にし,さらにいっそう有効に使われるように指導するのである。
しかし,このように,ものさしの使い方を指導する場合にも,常にものさしだけの指導をしていて,じゅうぶんであるとはいえないであろう。ものさしについての技能が確実になったら,次の学習の場では,それ以外の多くの技能が練習されるように指導されなければならない。たとえば,一枚の紙から,決まった大きさの紙を何枚か切り取ろうとする場合に,ものさしで寸法をはかることばかりでなく,その小さい紙が縦に何枚とれるだろうか,横に何枚とれるだろうか,全体としては,何枚とれるだろうかなどを問題にするように指導するのである。このようにすれば,ものさしの使い方からみれば,反復練習の機会であるにしても,これをとおして,長方形の面積を求める方法についての素地をつちかうところまで,学習を進めることになるわけである。このようにすれば,学習が単調になり,こどもが学習にあきることのないようにすることができる。
もちろん,初めから多くの技能について,練習させるようなことは,しないほうがよい。それは,学習に混乱をひき起し,練習の成果のあがらないことがあるからである。したがって,初めは,純粋に提示することが必要であることはいうまでもない。学習が進んで,その技能が確実になったときに,はじめて他の技能も組み合わせ,その場を複雑にしていくようにするがよい。現実の社会におけるものは複雑であって,決して単純ではない。学習が単純な場においてのみ指導されると,そのような学習の場で習得された技能は,実際の社会でじゅうぶんにその力を発揮することができないであろう。
以上述べてきたように,こどもにできるだけ練習の機会を多くつくってやり,しかも,その学習が,だんだんに複雑な場で行われるように指導されてこそ,はじめて,練習したことを,こどもは,いっそう有効に使うことができるようになるのである。
以上は,反復練習したことが,実際の場において,有効に使うことができるようにするために,どんなところに目をつけたらよいかを考え,その主要なものについて述べてみたのである。
8.教科書の使い方
| 教科書を,有効に使うには,どのようにしたらよいか。 |
教科書を絶対なものとして,忠実にページを追って指導していく方法は,既に過去のものとなった。今日においては,教科書を指導するのでなく,教科書によってこどもの生活を指導していくようにされなければならない。しかし,ややもすると,こどもの実際の生活とか,地域の生活とかにとらわれすぎて,教科書を軽視し,これを活用することを忘れ,無系統で,筋も骨もない場当り式の指導をしたり,また,数学的な内容のみにとらわれて,それを形式的に教え込んだりする傾向がないでもない。
そこで,教科書を有効に使うには,どのようにしたらよいかについて,教師の立場と,こどもの立場から述べてみようと思う。
(1) 教師は,教科書をどのように使ったらよいか。
教科書の使い方は,いろいろな角度から考えてみることができるが,ここでは,指導計画をたてたり,指導をしたりする手続からみて,どんなに有効であるかを述べてみることにする。
(a) 学級のこどもの実態からみて,教科書を使えば,どの程度に,その学級のこどもの必要に応ずることができるかを調べる
教師は,こどもの生活をよりよく指導するために,学年または学期のはじめにおいて,あらかじめ1年間または,1学期間の指導計画をたてることが必要である。また,さらに,この指導計画をたてるにあたって,教科書の中の教材で,どんなものが,学級のこどもの必要に応ずることができるかを,次のような観点から考えてみることも必要である。
○こどもの生活経験の範囲内にあるか
○こどもの必要や興味にあっているか。また,それが,学級の特定のこどもでなく,全体のこどもの必要や興味にあっているか。
○社会の必要,たとえば,生産・消費・保健・衛生・交通・通信・政治等の社会機能の面からみて,こどもに指導できるようになっているか
○学校や地域社会の特質から考えて,適当なものが取りあげてあるか
○学校や地域社会の行事などに適合しているか
○数学的内容と生活問題とが,うまく調和しているか
このような観点から教科書を調べ,教科書にあるもので,指導に使うことができる教材を選ぶのである。
(b) 不適当な教材があったら,その補助として,必要になる経験や教材を集めて,組織だてる
教師は前に述べたように,教科書の中に適当な教材があれば,それを,そのまま用いたり,また,修正して用いたりすることが必要である。しかし,たまには,こどもに問題とならない不適当な教材があることも考えられる。このような場合には,それにかわる必要な経験や材料を集めて,それを組織だて,指導するようにしなければならない。
たとえば,教科書に,さつまいものとれ高を比べたりして,重さの単位やはかりの使い方を指導する教材があったとする。このような場合に,事情によっては,それが実際に行えないことがある。このようなときには,こどもが直接に経験できるような学用品やその他の身のまわりの物の重さをはかることに関係のある教材にかえることが考えられる。また,一粒の種もみから,いく粒のもみができたかを調べながら,被除数が三位数や四位数で,除数が基数の場合の除法を指導する教材があっても,こどもに直接経験がなくて,理解が困難であると予想されることがある。このようなときには,こどもの生活経験や社会の必要にぴったりとあてはまり,しかも,同じ数学的な内容が,うまく調和して学習できるような教材,たとえば,単位時間に,電車に乗ったり,電車から降りたりするお客の人数を調べるような問題にとりかえることも考えられる。
(c) 計算やその他の数量関係について,適切に理解されるように提出されているかを調べる。もし,それが適切でなかったら,その補助的な指導を考える
こどもに,しっかりとした理解をもたせて,学習を進めていくためには,その指導の過程に飛躍がないように,理解の段階が分祈され,指導されるように計画されなければならない。
たとえば,四位数÷基数のわり算,(2034÷4)のしかたを理解させるためには,次のような段階が考えられる。
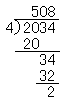
○被除数の相対的な大きさについて理解させる。
(2034は,1000が2個,10が3個,1が4個,または,100が20個,10が3個,1が4個)
○100の個数,10の個数,1の個数などを求めようとして,順序にわり算をしていく。20個(100の個数)÷4=5(100が5個ずつになる)。100が5個あることは,500であるから100の位に5を書く。
○余りがでたら,それが,除数より小さくなっているかどうかを,いつも確かめる。
また,小数の意味を理解させる場合には,次のような段階に分けることができると考えられる。
○金高,長さ,重さなどのように,10,100,1000などが,順次にその単位の間の関係を表わす数になっているときには,これらの単位で表わされた測定値は,そのうちの一つの単位で表わすことができる。
(2㎞と40は,2.04㎞と書ける)
○小数点の位置は,測定値を一つの単位で表わして,その単位名の位置を示している。
○小数点を使って表わした測定値についても,0は,整数と同じように空位を示している。(3円5銭は,3.05円と書く)
○小数点を使って表わした測定値は,整数と同じ法則によって,大小を知ることができる。
○ある位の単位の大きさは,その右の位の単位の大きさの10倍である。
○ある位の単位の大きさは,その左の位の単位の大きさの1/10である。
以上は,除法のしかた,および小数の意味について,その理解の段階を示したものである。このように,理解の段階が,こどもの発達に即して分析され,それが適切に提出されているかどうかを,教科書について確かめるのである。もし適切でないものや,理解事項として,おちているものがあったら,補助的な指導の計画をたてることが必要である。
(d) 教科書に使ってあることばを調べ,学級のこどもが,それを理解することができるかどうかを確かめる
教科書を読んで,こどもが学習を進める際に,そこに使われていることばが,むずかしくて,はっきり読みとれなかったり,またわからなかったりして,学習がうまくいかないことがある。たとえば,低学年のこどもには,「けいかく」ということばの意味がわからなかったり,あるいは「はじめのけいかくどおりにするには……」と述べられてある場合に,「はじめのけいかく……」が,どれをさしているのか,わからなかったりすることがある。
そこで教師は,このような誤りやすいことばや,わからないことばがないかどうかを, 学習を展開するにさきだって,あらかじめ調べておくことが必要である。もしも,学習の途中において,理解できないことばがあったら,これをわかりやすく説明するなどして,こどもの学習を援助するように,くふうすることが必要である。
(2) こどもは,教科書をどのように使ったらよいか。
ここでは,こどもが,教科書を学習に活用する場合に,どのようにしたらよいかについて,述べてみることにする。
(a) こどもは,教科書を参考書として,計算その他についての学習をする
こどもは,教科書の中に書いてある事がらから,どのようなことに問題をもち,その問題を解決するのに,どんな学習の計画をたてたらよいか,また,その計画に従って学習を進めるには,どんな方法をとったらよいかについて,暗示を受けることができる。また,自分の考え方と,教科書に書いてある考え方とを比べて,自分の考え方を確かめたり,あるいは,自分の考えつかなかったような,よい解決の方法を知ったりすることもある。また,教科書に,学習した内容をまとめてあるようなところがある場合には,自分が今までに学習した事項を整理するために,これを参考とすることもできるわけである。とにかく,このように,こどもに教科書の使い方をくふうさせ,有効に使えるようにすることは,指導上たいせつなことであるといえる。
(b) 教科書にある問題を用いて,計算などの技能を実際に適用してみたり,練習したり,また反復練習をしたリする
この学習のしかたについては,「有効な反復練習」で詳しく述べたので,ここでまた,述べる必要もないと思われる。しかし,こどもが教科書を用いて練習する場合のたいせつなことは,自分から進んで練習ができるようにし,しかも,いつも,自分の力を確かめて,次々に進むように指導することであるといえる。
以上は,教科書を,どんなに生かして使っていくかについて述べたのである。ここで注意しておきたいのは,上に述べたことはどのように教科書を修正して指導計画をたてたり,指導したりするかということについてであった。このようにしてはじめて,教科書を活用することができるのである。教科書をそのままに教えることが,教科書を活用することにはならないのである。