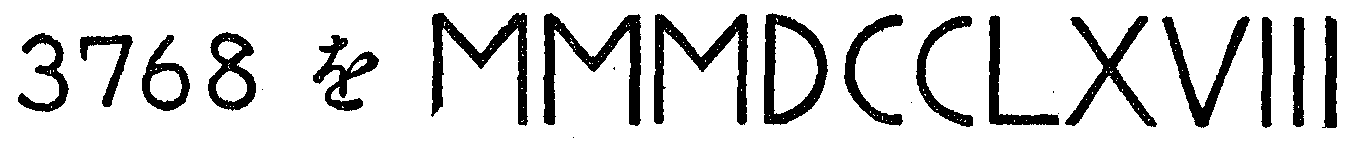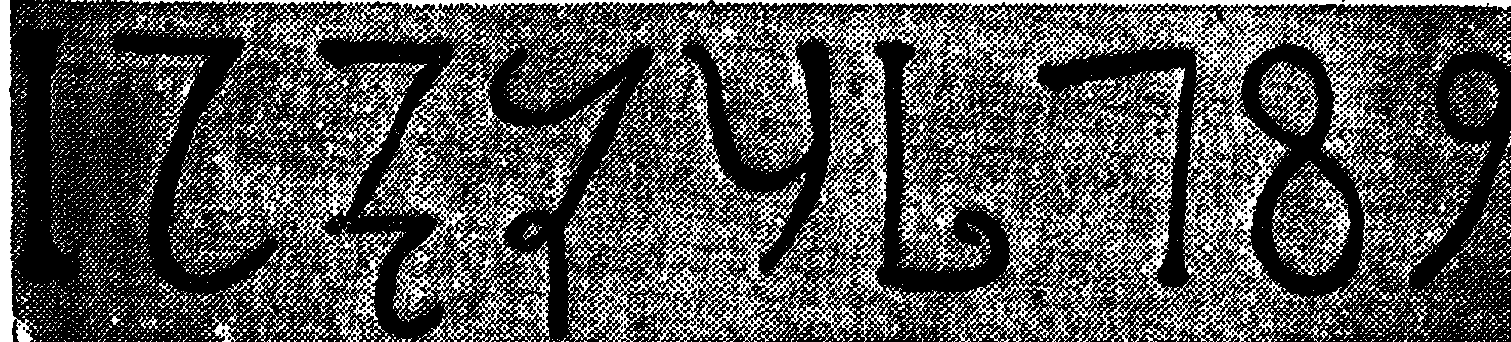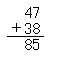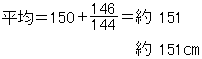Ⅱ. 算数科の一般目標
算数科の一般目標として,どんなものをあげることができるか。
Ⅱ.算数科の一般目標
算数科の一般目標として,どんなものをあげることができるか。
1.算数は,われわれの生活に,どのように役だつか。
2.算数は,教育の一般目標を達成するのに,どのように役だつか。
3.算数科の一般目標として,どんなものが考えられるか。
1.算数とわれわれの生活
人類の長い経験と努力によって現在の文化が作られてきたことは,ここに改めて言うまでもないことである。この文化の中でも,算数の発生は古く,その発展に従って,生活の改善に必要な考え方を生み出し,また,その考え方で処理するのに必要な,すぐれた用具としての役目を果してきた。
このような算数の生いたちを考えていくと,今までと同様に,現在も,また将来も,おとなの生活に役だつとともに,こどもの生活にも必要であることはすぐうなずくことができる。本節では,算数の基礎的な事がらについて,その発展の筋道を明らかにするとともに,算数がわれわれの生活に,どのように役だつかを述べることにする。
われわれは今日,命数法・記数法・計算・測定などを用いているが,その便利さになれすぎてしまっている。そのために,何が,どんなときに,どのように便利であるかということに,ほとんど注意しなくなっているといってもよいであろう。このように,算数が日常の生活にしみこんで生活化されたのは,先人の長い間のくふうのおかげであるということができる。
教師は,命数法・記数法・計算・測定・図形・用語などについての指導をするときに,これらのものが,どんなにすぐれたものであり,われわれの生活にどのような関係があるかを知っていることが必要である。それは,これらのことがらを学習すると,生活がどのように改善されるか,また,数量的な処理がどのように進歩するかが,はっきりわかるからである。
これがわかって,はじめて,算数の本質や価値が明らかにされるといえる。また,学習指導の方法は,これによって,有効適切なものとなるであろう。
(1) 命数法や記数法は,われわれの生活に,どのように役だつか。
(a) 命数法や記数法の組立とその進歩について
命数法とは,数に名まえをつける方法のことであり,数詞の組立といってよい。記数法とは,数を記録する方法のことである。現在,われわれが用いているような,便利な命数法や記数法が,大昔からあったのではない。現在,われわれが用いている方法と,大昔に用いられていた方法とを比べてみると,現在の方法が,どんなに便利であるかが明らかになってくる。
有史以前の数詞が,どんなものであったかは,明らかでない。しかし,未開人が今日用いている数詞を調べてみると,およその見当をつけることができる。次にあげるのは,今日,グリーンランド人が用いているといわれる数詞の組立方を書いたものである。かっこの中にあるのは,その意味を示したものである。
ひとつ, ふたつ, みっつ, よっつ
片手が終った(5),片手とひとつ(6),
片手とふたつ(7),片手とみっつ(8),
片手とよっつ(9),両手が終った(10)
ここまでくると,足の指に移っていく。
両手と片足のひとつ(11),
両手と片足のふたつ(12),‥‥‥‥,
両手と片足(15),
両手と片足とひとつ(16),‥‥‥‥,
ひとりの人が終った(20)
これは,命数法の一例であるが,大昔の人たちは,手近にあるものの名まえを,数詞として用いていたように想像される。
このような命数法では,すくなくとも,多くのものの個数を数えるのに,不便であったに違いない。
この不便さは,いくつかずつにくぎって数える方法が考え出されて,はじめて解決された。前の例にあげたように,人間の両手両足を用いて数えていく場合に,片手の指を使い終ったとき,つまり,5まで数えたとき,これを一くぎりにして数える方法が考えだされた。さらに,両手の指が終ったとき,つまり10まで数えたとき,これを一くぎりにして数える方法が考えだされた。
このように,いくつかずつにくぎって数える方法を,五進法とか,十進法と呼んでいるわけである。
現在も,未開人の中には,五進法と十進法をまぜて用いているものがあるといわれているが,われわれは,十進法を用いている。
さて,われわれが現在用いている数詞は,次のように,できあがっているといえる。
「いち」「に」「さん」「し」「ご」「ろく」「しち」「はち」「く」「じゅう」として,これを一くぎりにし,「じゅうといち」のことを「じゅう」と「いち」の間にある「と」をはぶいて,これを「じゅういち」といっている。
このようにして,「じゅうに」「じゅうさん」‥‥,として,「じゅう」が二つのことを「にじゅう」としている。これから先も同じように,「にじゅういち」「にじゅうに」としていく。「じゅう」が三つのことを「さんじゅう」,「じゅう」が四つのことを「しじゅう」としていき,「じゅう」が「とお」のことを,つまり「じゅうじゅう」のことを「ひゃく」として,「じゅう」の次のくぎりとしている。
このあとは,「じゅうひゃく」のことを「せん」,「じゅうせん」のことを「まん」,‥‥として,前のくぎりの10倍を,その次の大きいくぎりとしている。
これが,現在用いている十進法による命数法である。この方法は,次のようにやさしくまとめることができる。すなわち「いち」から「く」までの9個の数詞と,「じゅう」,「ひゃく」,「せん」,「まん」,‥‥の位をあらわすことばに,よせ算やかけ算で数詞を組み合せていくと,どんな大きな数でも,となえることができるようになっているといえる。
にじゅう=(じゅう)×2
じゅうご=(じゅう)+(ご)
にじゅうご=(じゅう)×2+(ご)
このようにして,比較的少ないことばで,非常に多くの数詞を組み立てることができ,となえることができるところに十進法のよさを認めることができる。
次に,記数法について考えてみよう。
ごくわずかな個数しか数えることができなかった大昔では,その個数を忘れないようにするのに,なわ結びや小石などを用いていた。大昔に,このような方法で数を忘れないように記録したであろうということは,現在でも未開人が,これらの方法を用いていることから想像することができる。この方法は,数えたものの個数を,そのまま,なわの結び目や小石に置きかえたというまでのことであって,数を記録するためのじょうずな方法であるとはいえない。
人類が進歩して,多くのものを数えたり,大きい数を取り扱ったりする必要が起ってくると,前に述べたような,小石やなわの結び目などを使っていたのでは,間に合わなくなる。そこで,昔の人たちは,大きな数を記録するのに,いろいろな方法をくふうしたのである。
そのいくつかの方法を,例としてあげてみよう。
エジプトでは,次のような記号を考え出して,数を書き表わしていた。
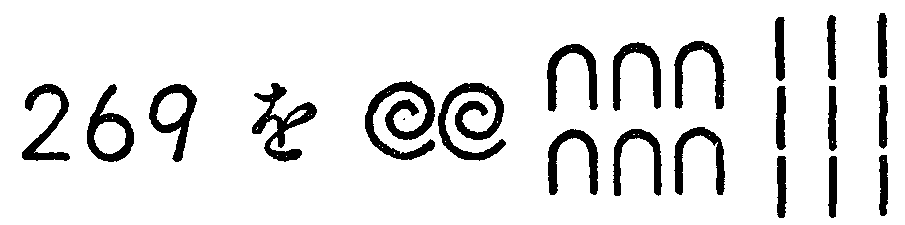
これは,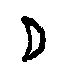 が10個で
が10個で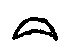 (10),
(10),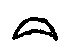 が10個で
が10個で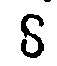 (100)と決めて書き表わしているのである。
(100)と決めて書き表わしているのである。
また,ローマでは,次のような記号を使って,数を書き表わしていた。
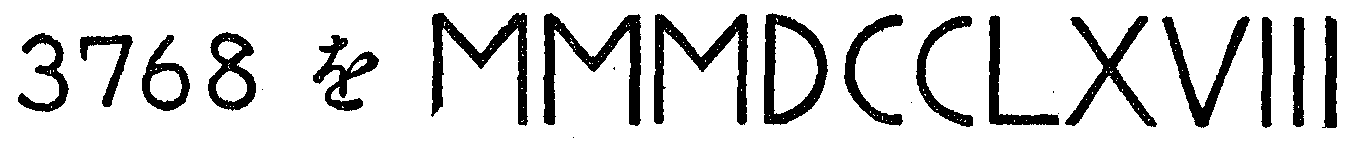
これは,1が5個でV(5),1が10個でX(10)とし,Xが5個でL(50),Xが10個でC(100)とし,Cが5個でD(500),Cが10個でM(1000)と決めて書き表わしているのである。
これらの方法は,前の説明でわかるように,数えるときの一くぎりごとに,新しい記号が用いられている。これらの方法は,数を記録しておくのに,小石やなわの結び目を使うのに比べて,やさしく記録しておくことができるという便利さをもった進んだ方法であるといえる。したがって,数を記録する場合に,今日われわれが用いている方法に比べて,記号が多かったり,記録する場所を広くとったりするだけで,さほど不便な方法であるとはいえない。
しかし,記録してある数を用いて,計算をすることになると不便である。よせ算やひき算をするときの不便さは,さほどでないにしても,かけ算やわり算になると,非常に不便さが目だってくる。
今日,われわれが用いている数を記録する方法は,インド人によって考え出されたもので,世界各国で用いられている。
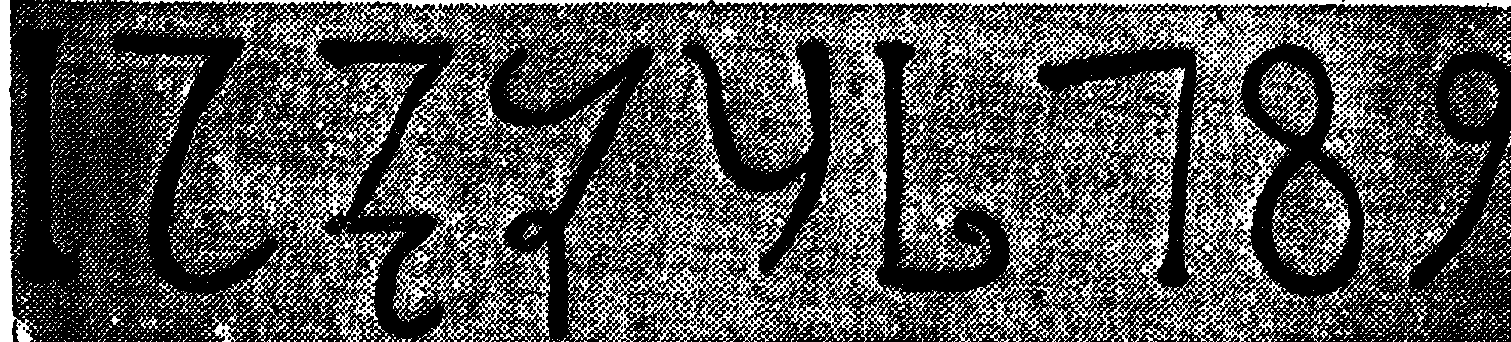
これは「いち」から「く」までを表わす9個の数字,1,2,3,4,5,6,7,8,9と,空位を示す記号「0」とを用いて,数を書き表わす方法である。つまり,右から左へ,順次に一,十.百,千,万,‥‥,の位に,それぞれ,0から9までの十個の数字を書いて,数を書き表わすのである。
このようなきまりに従えば,どんな大きな数でも,0から9までの十個の数字だけで書き表わすことができて,ことさらに,くぎりを示す記号を必要としない。したがって,数を記録する場合にきわめて便利である。このように便利になったのは空位を示す記号として,0が見いだされたからであり,これによって,位取りがやさしくできるようになったからである。
(b) 十進法が考え出されて,個数がどんなに多くなっても,たやすく数えられるようになった
ものの個数を数えるとは,数えようとするものに,数詞を順次に一つ一つあてはめていき,最後のものに与えられた数詞によって,そのものの個数を表わす手続である。
数えるときに,十進法を用いると,あてはめる数詞が規則正しいので,簡単に数えることができる。
すなわち,ものを数える場合には,まず,10個ずつのグループにまとめる。このようにすると,10個ずつのグループがいくつあるか,そのときの端数がいくつあるかで,簡単に数えることができる。
次に,この10個ずつのグループがたくさんできた場合に,さらに10個ずつまとめていくと,どれも,100個のグループになる。これによって,100個のグループがいくつあるか,10個のグループがいくつあるか,その端数はいくつあるかで,個数を知ることができるのである。このように,今までと同じような手続を続けていくと,どんな大きな数でも,容易にその個数を知ることができる。
この数え方は,数詞を順次にものにあてはめていく数え方に比べて,次のような便利さが考えられる。
(ⅰ) 10個までのものを数えるだけで,すますことができる。
(ⅱ) 10個数えるごとに,数える仕事が一段落する。したがって,数え始めてから,数え終るまで,ずっと注意を集中し続けなくてもよい。
(ⅲ) 数え違いがあったような気がして,数えなおす場合でも,10個だけを数えなおす手数ですますことができる。つまり,初めから、すっかり数えなおさないですますことができる。
このようなわけで,十進法による数え方が考え出されたおかげで,ものの個数がいかに多くなっても,あまりむずかしい操作をしないで,気楽な気持で,数えることができるようになった。
(c) 記数法が進歩して,どんな大きな数でも,かんたんに記録ができ,また,かんたんに数の大きさを比べることができるようになった
ものの個数を記録するには,前に述べたように,ものを10個ずつまとめる方法で数えていき,端数がなければ0,端数があれば,その個数を数字で順次に,左に書き並べて行く。
この記数法では,0,1,2,‥‥,9までの10個の数字の書いてある位置によって,その大きさが違う。これは,左のほうに順次に,1,10,100,1000,‥‥を単位にして書き表わされているからである。
したがって,どんな大きな数でも,0,1,2,‥‥,9の10個の数字と,規則正しい単位の大きさをもとにすることによって,書き表わすことができる。
一万五千三百二十五のように,漢字で数を書くと,万,千,百,十の単位の大きさを示すことが必要となる。ローマやエジプトで用いられた方法でも,これと同じように,各位の大きさを示す記号が必要であった。これと比べてみると,位取りの原理に従っての数字による記数法は,どんなに便利なものであるかがわかる。
位取りの原理を用いての数字による記数法は,数を記録するのに簡単で便利であるだけでない。これを,いくつかの場合をあげて,説明してみよう。
数の大きさの程度は,「何けたの数」というように,数を,位取りの原理に従って書き表わした数字の個数によって表わすことができる。また,これによって,数の大きさを,やさしく比べることもできる。この方法を述べると次のようになる。
(ⅰ) 数字の個数に違いのあるときには,数字の個数の多いほうの数が,個数の少ないほうの数よりも大きい。
(ⅱ) 数字の個数が同じであるときには,はじめの数字の大小で,二数の大小がきまる。はじめの数字が等しい場合には,次の数字の大小できまる。これも等しい場合には,第三の数字というようにして,比べることができる。
たとえば,5324と10281,580269と580517とは,次のようにしてやさしく大小をくらべることができる。
百の位の2,5を比べると5のほうが大きい。したがって,580517のほうが大きい。
このほかに,位取りの原理による記数法は,四則計算,特に,かけ算やわり算をするのに,最もすぐれたものである。これについては,あとで述べることにする。
なお,数を読んだり記録したりするのに,わが国で古くから用いられている用語がある。すなわち,それは,「いち」「じゅう」「ひゃく」「せん」であり,この次の位に「まん」という新しい用語が用いられ,「じゅうまん」「ひゃくまん」「せんまん」が用いられている。これは,位取り記数法に比べて,前に述べたように不便なこともあるが,10000000を千万と書くことができることを考えると,便利な場合もある。
(d) 命数法や記数法が進歩して,数を他の人々にやさしく伝えることができるようになった
数のとなえ方や書き方が,規則正しく簡単で,しかも,書き表わされている数が読みやすく,それが表わしている数の大きさも,すぐ知ることができるので,数を,他人にやさしく伝えることができるようになった。特に,どんな大きな数を書くにも,わずか10個の数字ですますことができるので,近代の通信機関を利用して,ある数値を他人に伝える場合でも,簡単に,しかも速く伝えることができるわけである。
とにかく,位取りの原理さえわかれば,どんな大きな数でも,やさしく取り扱うことができるといえる。
今日位取りの原理を用いての十進法による命数法や記数法が,世界中どこでも用いられるようになったのは,今までに述べてきた便利さがあるからである。
(e) 命数法や記数法は,こどもの必要にこたえるものである。
こどもたちは,学校に入学する前から数えることが必要な実際の場に当面している。これは,幼稚園のこどもなどをみれば明らかなことである。したがって,このような点から考えてみると,こどもたちは,数える必要を感じているといえる。こどもたちが,数える必要を感じてくると,もっと多くても数えることができるようになりたいとか,数を記録したり読んだりすることができるようになりたいとか,いろいろと考えてくる。また,こどもたちは,困難な場に当面して,このような必要を感ずることも考えられる。このような意味から,命数法や記数法の指導は,こどもの必要にこたえるものであるといえる。
(2) 計算は,われわれの生活に,どのように役立つか。
(a) 計算の意味とその進歩
計算が,社会科やその他の教科の学習に必要であり,また,こどもたちの日常生活にも必要であることは,いうまでもない。その計算をうまく指導するには,計算の組立と,そのよさをじゅうぶん知っていることが必要である。
計算はものの個数を数える一つの方法であり,直接数える方法を改善したものである。言い換えると,直接数える手数をできるだけ少なくして,その数えたものを用い,機械的な操作によって,結果を求める手続である。
実際の生活で,いくつかのグループのものの個数から,全体の個数を知ることが必要になる場合がある。これを簡単にする手続が加える計算であり,場合によってはかける計算である。また,一つのグループを,いくつかのグループに分けることが必要になる場合がある。これを簡単にする手続がひく計算であり,わる計算である。
大昔の人々は,計算をするのに,指や小石などを用いたであろう。また,数が小さいとか,簡単なものである場合には,暗算を用いたこともあろう。
しかし,数が大きくなってくると,このような方法だけでは、その目的を達することができなくなる。
そこで,計算の能率をあげようとして考えだされたのがそろばんである。そろばんは,ずっと昔から使われていたといわれている。ロンドンの大英博物館に保存されているものは,ローマ人が使ったもので,そろばんの中では,世界で最も古いものであるといわれている。
そろばんによる計算の特長は,よせ算やひき算が速くできるところにある。西洋では,筆算が盛んに使われるようになるとともに,そろばんは,そのかげをひそめていった。
わが国では,明治の初めに,西洋の算法を取り入れるまで,主として,そろばんによる計算が行われていた。それは,位取り記数法がなかったので,筆算が進歩しなかったためであると考えられる。しかし,筆算が使われるようになった今日でも,そろばんは用いられ,その長所を発揮している。
最近,さらに進んだ計算機が発明され,かけ算,わり算も楽にできるようになってきている。
西洋で,位取りの原理を用いた記数法が使われ,それによる四則計算の方法や形式がくふうされ,完成されたのは,だいたい15世紀のころであったといわれている。
そこで,この位取り記数法の原理を用いたこの計算の方法を,具体的な例によって述べてみよう。
記数法が進歩したために,0,1,2,‥‥,9の10個の数字を用いて,どんな大きな数でも書き表わすことができることは,前に説明したとおりである。それは,ものを順次に,10個ずつのグループにまとめていき,1,10,100,‥‥などにまとめたグループの個数を,順次に左のほうに書きならべていく方法である。
たとえば,47人と38人の二つのグループがあるときに,合計が何人になるかを知りたいことがある。この場合に,よせ算を知らないものは,一方が47人であるから,その数をもとにして,他のグループの人数をひとりずつ数えたしていくであろう。もっと幼稚な方法をとるとすれば,二つのグループを一つにまとめ,47人と38人であったことを,全く用いないで,初めからひとりずつ数えていくであろう。
この二つの数は,それぞれ,10が四つと1が七つ,10が三つと1が八つからできていると考えられる。したがって,それをあわせたときの10個のグループと,あとの個数を求める方法が計算であるといえる。
ここで,個数を数えるときと同じように,10個のグループにまとめることを考える。すなわち,7と8では10以上になる。そこで,10個のグループを作ると,10個のグループが一つと残りが5個になる。10個のグループの個数は,一の位の計算で出てきた1個と,それにもとからあった4個と3個とをあわせて,8個になる。このようにして,人数の合計が85になることがわかる。
| この計算の方法を,形式にまとめたものが,右に書いたようなよせ算の筆算形式である。 |
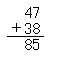 |
(b) 肉体的な労力をできるだけ用いないで,個数を知ることができるようになった
計算を用いると,直接ものについて1個ずつ数えるよりも,肉体的な労力を節約することができる。これを,具体的な例によって説明してみよう。
(ⅰ) 各学年の人数は,次のようであるとする。
178, 175, 176, 178, 175, 179
この学校のこどもの合計は,まず,よせ算で求めることができる。しかし,かけ算を合わせ用いると,ずっと計算の手続が簡単になる。
すなわち,175×6+(3+1+3+4)あるいは170×6+(8+5+6+8+5+9)として,計算することができるからである。
(ⅱ) 次の表は,身長についての平均を求めるために作ったものである。手続が,どんなに簡単になるかを示すために,㎝を単位にして,身長を表わしたものを用いた。
|
身 長
|
人 員
|
150との差
|
差×人員
|
|
161㎝
160
159
:
:
:
151
150
149
:
:
:
142
|
1
2
0
:
:
:
4
6
5
:
:
:
1
|
11㎝
10
9
:
:
:
1
0
−1
:
:
:
−8
|
11㎝
20
0
:
:
:
4
0
−5
:
:
:
−8
|
|
合 計
|
144
|
|
過〜不足
146
|
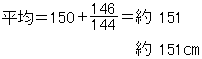
そこで,この表を用いて,150を平均とみなし,これを修正する方法によって,平均を計算する。
このような方法を使えば,大きな数をそのまま取り扱って計算する必要がなく,ほとんど,暗算でできるくらいの計算になってしまう。
(ⅲ) 次に178×367の計算について考えてみよう。
かけ算を用いて,下にあるような結果が得られたとする。
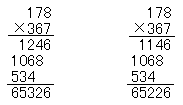
この二つの計算で,どちらが正しいかを確かめる方法を考えてみよう。
まず,初めから,計算をしなおしてみる方法が考えられる。また両方の部分積を比べ,178×7の部分積に違いのあることがわかり,これを確かめてみる方法も考えられる。この二つの確かめる方法を比べてみると,計算の過程が明らかに示されているときには,後者の確かめ方のほうが,どんなに確かめるための労力を節約することができるかは明らかである。
(ⅳ) 一箱に,みかんが178個ずつ入れてある。それが367箱あったら,みかんの総数はどれだけになるかを調べることについて考えてみよう。
これを,1個ずつ数えて,65326個あるとしたものと,65226個であるとしたものがあった場合に,どちらが合っているか,また,どちらも違っているかもしれないなどと考えられる。そこで,これを調べるには,どんな方法を用いたらよいだろうかが問題になる。
もし,かけ算を知らないとすれば,もう一度初めから数えなおしてみるよりしかたがないだろう。また,かけ算を知っているとすれば,正しい総数を知るのに,簡単に確かめることができるわけである。
(c) 精神的な労力をできるだけ用いないで,個数を知ることができるようになった
計算は,ものについて直接数えるかわりに,機械的操作を用いる方法であることは,前に述べたとおりである。計算の原理が理解でき,その理解の上にたった九九を記憶しておれば,ものに即して直接数えなくとも,その個数を知ることができる。
この方法は,ものに即して数える方法と比べて,ずっと,精神的な労力を節約することができるといえる。
(d) 計算の使い方が理解でき,また,式を用いることができれば,計算に用いられている思考や資料を,他人に伝えることができたり,また,反省したりすることができる
数量を使って,ものごとを処理するときに,式やことばを用いて,結論を導いた方法や,その過程を表わすことができる。これと同時に,結論を導くために用いた資料も表わすことができる。したがって,その式やことばを見れば,結論を導くのに用いた自分の思考や資料を反省したり,また,場合によっては誤りを正したり,方法を改善したりすることができる。また,自分が結論を導くために用いた方法や資料を,他人にわかりやすく伝えることもできるわけである。
(e) 計算は,こどもの必要にこたえるものである
ものの個数を知るのに,一々数えていくことは,手間のかかることである。手間がかかるということは,それだけ肉体的にほねのおれることであり,精神的にもずっと緊張し続けていかなければならないという点から考えて,労力を要することである。
このようなことは,こどもといえども望むはずはない。したがって,結果が簡単に求められるという計算は,当然,こどもの必要にこたえるものであるということができる。
また,こどもは,自分の考えの筋道をうまくたてていったり,その考え方を,もっとよいものにしたいと思っている。また,他人の結論そのものだけでなく,その結論を導くのに用いた方法や資料についても,知りたいと思っている。このような面を考えても,計算や式やことばで言い表わすことは,こどもの必要にこたえるものであるといえる。
(3) 量の測定は,われわれの生活に,どのように役だつか。
(a) 量の測定の意味
測定は,量の大きさを,数で表わすための操作であるといえる。
ものの個数を数えることも,量の大きさをはかる測定の一つの方法であり,最も素ぼくな方法の一つである。出席人数や欠席人数は,出席や欠席について測定した値であるといえる。今日では,長さや重さなどの量を測定するために,進んだ道具や方法があるが,これらの道具や方法は,大昔からあったのではない。人類が生活の必要から,それを満たすために,いろいろと,測定する道具や方法を進歩させてきたのである。
人類がまだ,野生の植物や動物に依存して,生活ができた時代には,量を考えたり,また,量を測定したりすることは,あまり必要がなかったと思われる。
その後,物をたくわえておいて,あとで使ったり,また,食物を栽培したり飼育したりなどして,生活をしなければならなくなった。このようになると,いきおい,生活のための計画をたてることの必要に迫られ,量を測定することが行われるようになったと想像される。
しかし,初めのうちは,自分で決めたいれ物を使って穀量をはかったり,また手足など身体の一部分の長さをもとにして,いろいろなものの長さをはかったりして,必要を満たすことができたようである。これらのことは,つか,ひろ,フートなどのことばから想像することができる。つまり,自分で選んだものを単位にして,それの何倍あるか,また,その長さのいくつ分にあたるかというようなことがわかればよかったのである。
しかし,このように,めいめいが,そのときどきに都合のよいものを単位にして,量の大きさを表わすのでは,その量の大きさを,だれにもわかるように表わすことができない。そこで,この不便さを取り除くために,単位にとる大きさをきっちりと決め,この単位を使えば,だれでも,量の大きさを同じようにとらえることができるようにくふうしたのである。これが,今日,われわれの社会で用いられている主要な測定単位であるといえる。しかし,いつもこのような測定単位を用いなければならないというのではなく,場合によっては,身近にある適当なものを単位として量の大きさを表わすことも,測定の方法として重要な点であるといえる。つまりこれは,そのもとになっている大きさがわかっておれば,きわめて手軽であり,場合によっては,これでじゅうぶん測定のねらいを達することができるからである。
(b) 単位が統一され,量の大きさを他人に正しく伝えることができるようになった
人類は,初め,ものの個数を言い表わすのに,「たくさん」とか「すこし」とかいうことばを用いていたが,測定をする必要がおきた場合にも,その結果を表わすのに,このようなことばを用いたであろうと考えられる。
暑さ寒さを言い表わす場合でも,初めは「きょうはきのうよりもすこし暑い。」とか,「昨日よりも暑さがひどい。」とか,また,「この二,三日,ずいぶん寒い。」とかいうように,自分の感じで言い表わす以外には,表わす方法がなかったと考えられる。もちろん,現在でも,このような言い表わし方を用いる場合もあるが,温度計や湿度計が発明されて,「きのうは26°であったが,きょうは30°だ。暑いわけだ。」とか,「どうも蒸し暑いと思ったら,湿度が80%もある。」というように,暑さ寒さを,できるだけ客観的にとらえようとして,言い表わすことができるようになった。
さて,量の大きさは,これを表わすための単位と,その単位ではかったときの数値で言い表わすことができる。しかも,この単位をきめておけば,数値は,おのずからきまってくるはずである。測定で最もたいせつなのは,単位である。
しかし,このような単位は,ずっと昔から統一されていたわけではなかった。わが国でも,江戸のころは,地域によってその単位が違ったり,また,仕事によって,単位の大きさが同じでない場合があったようである。十五世紀ごろのローマ帝国の末期には,長さの違ったピエ(ローマのフート)という単位が,200種もあったといわれている。これでは布100ピエで金額がいくらといっても,長さが客観的になっていないから,その布の価値も,客観的にならない。したがって,布などを売買する場合には,いろいろ困難な点が多かったろうと想像される。
ところが,交易が盛んになり,生産物が商品化されてくると,品物を取り引きするために,共通の大きさを単位にとることが必要になってくる。
さらに,この交易が世界的になってくると,どの国とでも簡単に取り引きできるようにするために,いわゆる国際的な単位の必要が考えられる。1875年に万国度量衡条約をつくり,世界共通の単位として,メートル法が採用されたのは,前に述べた必要にこたえたものであるといえる。
さて,このように,測定単位が国際的に統一されると,測定した人に関係なく,同じ数値で表わすことができる。したがって,単位の大きさが国際的に決められているから,この単位を使っていろいろな量を表わすと,地球上のどこの国の人にも,量の大きさをまちがいなく伝えることができるようになったといえるわけである。
このように,国際的な単位が生れたことは,国際貿易や,分業による生産方式に大きな影響を与えただけでなく,地球上の人々が互いに協力していくことができるようになったところに,その真の意義を見いだすことができる。
(c) 測定が進歩して,量の大きさを,手軽に知ることができるようになった
昔の人は,土地の広さを知ろうとするときに,まわりの長さをはかる方法として,歩測を用いたといわれる。歩測によって,詳しくはかろうとすると,一歩の歩幅が,きまった長さになるようにくふうをしなければならない。また歩幅を一定にするためには,相当に練習もしなければならなくなる。
われわれは,このような場合に,巻尺を用いて測定をしている。巻尺を用いて測定するには,全く測定する技術がいらないというわけではないが,その技術は,詳しく歩測するための技術にくらべて,ずっとやさしいといえる。
したがって,現在では,巻尺を用いることによって,土地などの長さを手軽に測定できるようになったといえる。
また,重さをはかる場合でも,ずっと以前には,もっぱらさおばかりを用いていた。さおばかりを用いるのでは,はかろうとするものの重さによって,おもりをつるす位置を決めなければならない。その位置を簡単に決めることができるようになるためには,相当の練習が必要である。ところが,ぜんまいを用いたはかりでは,ただ,物をつるしたり,台の上にのせたりするだけで,重さを測定することができる。したがって,ぜんまいを使ったはかりを用いることによって,重さを手軽に測定することができるようになったということができる。
このほか,とけいを用いると,時刻や時間が簡単Kわかるということも,前に述べたことと同様に,測定がきわめて手軽になってきているということができる。
(d) 測定が進歩して,量の大きさを,いっそう詳しく知ることができるようになった
量の大きさを,必要に応じて,いっそうくわしくはかることができるようになった。これは,計器の進歩によるものである。
手軽に秒の十分の一まではかることができるストップ・ウォッチ,短時間で体温を知ることのできる体温計,薬品などの調合に,その微量を測るために使われるてんびんなども,その例である。
このように,すぐれた計器を考案して,いろいろな量をいっそう詳しく測定できるようになったとともに,その詳しい測定値を,数に書き表わすことも,できるようになった。
米の量を表わす場合に,最近まで,ます目による表わし方がよく用いられていた。しかし,これは,たとえば1升ますに一ぱいの米といっても,米の入れ方で,その量が多かったり少なかったりする。したがって,この表わし方では米の量を詳しく表わすことはできない。そこで最近では,米の量を重さで表わすようになってきた。しかし,ますは,必要な米のおよその量を知るのに便利であるから,家庭では今でも,これを用いて,米の量を測定している。
この例から考えても,人々は社会生活が正しくできるように,計器をうまく利用して,測定値を必要に応じて詳しく知ろうと努力していることがわかる。
(e) 測定は,こどもの必要にこたえるものである
量の大きさを測定しても,測る人ごとに測定値が違うようでは,こどもたちといえども喜ばないところである。
このようなことでは,たとえば,めいめい,一つの物の部分を受け持ち,これを作って,一つの物を組み立てようとしても,組み立てることができないからである。
また,こどもたちは,測定の手続が手軽であることも望んでいるところである。このように考えると,測定単位がだれにもわかるようなもので,取扱が簡単であることと,測定の手続が手軽であるということは,こどもの必要にこたえるものであるといえる。
(4) 図形は,われわれの生活に,どのように役だつか。
(a) 物の形や構造を表わすのに,図形が用いられる。また,図形を見ると,実物を見るような感じをうけるので,図形を用いると,物の形や構造を,やさしく他人に伝えることができる
遠方にある物や,簡単に見ることができない物を,見ることができたときに,見たままを,図にかきとめておくことがある。このようにしておけば,あとで必要になった場合に,その図を見さえすれば,実際の物を前にしていると同じように,ある程度のことは調べることができる。
とにかく,現存していない物でも,これを,かき残された図で調べたり,外国の様子を図や写真で調べたりすることができるのは,図形が,物の形や構造を示すのにすぐれているからである。また,これから作ろうとする物の設計図をかくと,それが実際にできあがったときの様子を,やさしく想像することができて便利である。また,このような便利な図形が考えられるので,これから作ろうとする物についても,図の上で,いろいろとくふうすることができる。
また,このような図形は,図をかいた人だけに役だつばかりではない。これを用いて,自分の考えを他人に伝え,他人の参考になるように役だてることもできる。これは,図形が前に述べたような特質をもっているからである。
建築家の設計図や,研究者の報告書の説明図などは,このような場合に用いられたよい例であるといえる。
(b) 量の大きさについての関係を,図形で示すと,視覚に訴えて考えることができる。したがって,図形は,考えを進める上に有用なものである
前に述べたように,設計図が,形や構造を示すことのできるのは,直線や曲線,平面や曲面などによって長さ・面積・体積・角度などの量の大きさの関係を示すことができるからである。しかも,この図によって,自分の考えを進めていくことができることは,前に述べたとおりである。
このような設計図などとは別に,数量についての関係を示すのに用いられる重要な図がある。
統計的な数値を,図で表わす場合が考えられる。普通,グラフと呼ばれるものはこれにあたる。
棒の長さで量の大きさを表わし,それらの量の大小を比べやすくする棒グラフ,円で全体の大きさ,扇形で部分の大きさを表わし,それらの量の割合を比べやすくする円グラフ,これと同じような考えで用いられる帯グラフ,正方形グラフ,また,量の大きさの変化をわかりやすくする折れ線グラフなどがこれである。
このほかに,文章の筋道や,概念の関係などを,わかりやすくするための図もある。このような図を用いると,ただ頭の中で考えるよりも,やさしく考えを進めていくことができる。
問題解決の場合に,図を用いることがある。これは,今述べたような理由によるものである。
(c) 位置の関係や,連結の様子は,図形で示すことができる。図形は,位置を示したり,道案内をしたりするのに有用なものである
なれない場所を歩くときに,最も役だつのは地図である。土地の様子がわからないときに,これを図で示してもらうと,非常にわかりやすくなる。
したがって,地図を用いると,位置や道順,方向や距離などを,簡単に知ることができる。これは,地図が,実際の土地の様子を縮めてかいた図であるからである。つまり,どの長さをとっても,実際の長さを同じ割合で縮めてあるからである。
大きな建物や広い複雑な土地は,現地で見ても,なかなか全体の見とおしがつかないものである。このような場合に,縮図や地図を用いると,現地で実際に見るよりも,かえって,わかりやすくなることがある。
また,道案内をする場合に,ことばだけでするよりも,案内図を用いるほうがよくわかる。これは,図を用いると,道などの連結の様子を示すことができるからである。
(d) 図形は,いろいろなもののデザインをするにも役だつ。
普通に用いられている図形は,整ったものが多い。これをうまく配列すると,いろいろの美しい模様を,作ることができる。

基礎になる図形のかき方や性質についての知識をもっておれば,複雑な物の形や構造を取り扱うにも,また,数量関係を図に表わして,それを研究するにも便利である。また,美しい模様のデザインをするにも役だつ。
(e) 図形は,こどもの必要にこたえるものである
こどもは,いろいろな物を手分けして作ったりすることがある。このような場合に,その物の形や大きさを.お互に話し合って協力することが必要になる。この場合に,図形を用いるとき,自分の考えをやさしく示すことができるし,また,自分の考えている案を他人にやさしく伝えることができる。このようなことを考えると,図形は,こどもの必要にこたえるものであるといえる。
また,友だちに自分の家までの道順を話したり,また,へやに,いろいろなものを配置する必要が起る。このようなときにも,こどもは図形の必要を感じる。このような点から考えても,図形は,こどもの必要にこたえるものであるといえる。
(5) 用語や記号は,われわれの生活に,どのように役だつか。
(a) 用語や記号の意味
ものごとを,はっきり言い表わすには,そのときに用いることばの内容が,すでに,きっちりと社会で認められているか,さもなくば,その意味を,きっちりと決めておかなければならない。
算数は,数量的な事がらを,正確に,的確に,しかも能率的に処理することを目的としている。したがって,算数で用いられる重要なことばの内容が,きっちりときめられていなかったら,その目的を達することができない。つまり,ことばの内容があいまいであったのでは,事がらを正確に,しかも的確に表わすことができなくなるとともに,処理することもできなくなる。
まして,理解するのに,ほねがおれるようなことでは,処理の能率があがらないのは,当然のことである。
したがって,重要なことばは,特にまちがいの起らないように,その意味がきっちりと決められていることが必要である。この意味のきっちりと決められていることばを,用語といっている。
用語を,こどもの場合も成人の場合も,同じにしたのでは,かえってわからなくなることがある。たとえば,長方形と直方体を,低学年では,いずれも長四角とよび,正方形と立方体を,いずれも,ましかくと呼んでいる。
低学年のこどもには,このように用いても,不便を感じないのである。いわば,低学年のこどもは,正方形と立方体とを区別して考えねばならないまでに,図形についての分析を必要としないからである。学年が進んでくると,平面と立体とが区別できるようになる。言い換えると,平面図形と立体図形とに分析して考えるまでに,こどもが発達してくるのである。
いわば,厚みが問題ではなくて,その表面の形だけをとらえていけばよい場合に当面したり,また,その厚みも考に入れて,物の形をとらえていけばよい場合にも当面したりするのである。ここではじめて,ましかくということばの意味内容を,立方体と正方形とに分析して考えることが必要になり,また,それを表わすことばも必要となるのである。
このように用語は,成人の使用しているままに用いるというよりも,成人が使用しているように導くことがたいせつである。すなわち,ふじゅうぶんながらも,こどもながらにじゅうぶん分析した内容をもとにして,それを表わすことばを,用語としたいものである。
このように,こどもの知能の発達に従い,成人から見て,ふじゅうぶんなところを修正し続けていき,だんだんに成人が用いる用語に導くのであるから,その過程に用いられることばも,ここでは用語ということにする。
記号についても,用語と同じようなことがいえる。記号の場合には,用語の場合と違って,用いるものは同じであるが,その記号の示す意味内容に差異が認められる。等号=にしても加法の記号+にしても,初めは,ことばの代用として用いていく。そのうちに,ことはの意味がきっちりと限定されてくるに従って,その記号の意味も,きっちりとしたものになってくる。
(b) 用語や記号を用いて,ものごとを表わすと,物事をきっちリ記録しておくこともできるし,他人にまちがいなく伝えることもできる
次のような若い教師の学級日誌があった。
学年共同で,計算練習のプリントを作る。
部数142を注文した。
桃組45名,かつら組45名,たちばな組46名で,どの学級も2部ずつひかえをおくから,45+45+46+2×3=142となる。
1部40円,140部代の請求(2部おまけ)
生徒ひとりの負担は41.18円
40円×140=14×400=5600円
5600円÷(45×3+1)=41.176円……41.18円
桃組とかつら組の負担は,1853円ずつ,(41.18円×45=1853.1円)
たちばな組の負担は,1894円(41.18円×46=1853.1円+41.18円=1894.28円)
1853円+1853円+1894円=5600円
41.18円は端数があり,集金がめんどうであるから,円以下の端数は切り上げて,42円ずつ集める。残金は,学級費の中にくり込むことにした。
この計算は,生徒たちに請求書を見せ,いっしょに計算しながら,個人の負担額と,学級の負担額をきめた。こうして,生徒の当番が集金して,印刷屋に代金を支払い,受取書をもらったのである。
この記録で,適当な用語や記号を用いていなかったら,これによって,家庭に,この会計の様子を正しく伝えることができない。用語や記号を正しく用いて,考えの筋道を表わしていてこそ,このねらいを達することができるのである。
この例を見ても,用語や記号を正しく用いると,ものごとを,きっちり記録しておくことができるし,また,他人に対しても,その様子を,まちがいなく伝えることができる。
(c) 用語を用いると,自分のもっている考えを整理することかできる。また,ものごとを厳密に考えることができる
一般に,用語は具体的なものから抽象化し,一般化したものである。たとえば,正方形という用語について考えてみよう。
正方形の大きいもの,小さいもの,また,その表面にいろいろな色がついているもの,水平においてあるもの,水平面に垂直な平面の中にあるものなど,これらから一般化して出てきたものが,正方形という用語である。したがって,用語は,こうした種々の具体的な事実にうらづけられているので,いろいろなものを整理することができるわけである。いわば,用語を指導するときに用いられた具体的な事実から,その他の具体的な事実に対して,正方形という用語を用いることができ,これで,具体的なものを整理することができるのである。
また,用語を用いようとすると,ものごとに対して厳密に考えることが必要になる。たとえば,正方形という用語を用いようとすると,その四角の辺がまっすぐであるとみることができるか,頂点の角が,どれも直角であるとみることができるか,辺の長さはどれも,同じであるとみることができるかを考えなければならなくなってくる。いわば,こうしたことから,用語の意味が,きっちりと決められてくるにつれて,だんだんに,ものごとを正確に考えなければならなくなってくる。
(d) 用語や記号は,こどもの必要にこたえるものである
こどもは成長するにつれて,いろいろな事実に当面するのであるが,これを整理していかないと,これにうまく対処していくことができない。二つのグループをあわせて数えるにしても,増加したとき,違いがわかっているときなどと,多くの事実に当面する。これを,一つ一つ違ったものと考えていたのでは,こどもといえども,やりきれるものではない。これを,すべて,よせるという用語や,+という記号によってまとめることができて,これらのものを簡単に処理することができるのである。
また,こどもは,協力して仕事をしていかねばならない。そのときに,意味内容のはっきりと決まった用語や記号がなかったのでは,お互の考えを,まちがいなく伝えることができないので,協力することが困難になる。
このようなことを考えると,用語や記号を正しく使うようにすることは,こどもの必要にこたえるものであるといえる。
こ の 節 の む す び
人類は,生活を合理化しつつ,よりよい生活を常に求めてきた。その一面として,数量関係をとらえ,これを正確に,的確に,能率的に処理しようと努力してきたといえる。したがって,このような必要から,これまでに述べてきたような,命数法や記数法・計算・測定・図形・用語や記号などに対して,改善を加え続け,今日のようなすぐれた方法や原理を生みだしてきた。その結果,数量関係をやさしく,手軽に,必要に応じて処理できるようになったのである。
算数が,以上のように,人類の進歩に伴って生れてきたものであってみれば,今日のこどもにとっても,必要なものであり,また,役だつものであるといえる。
こどもは,これまでの人類の進歩を受けつぎ,更にこの向上に貢献していく使命を持っている。つまり,こどもが環境にはたらきかけて,自己を更新していくとともに,われわれの現在の思考や行為を改善していくべき使命をも,になっているのである。
算数科は,このような必要にこたえようとするものである。
したがって,このような意味から,こどもは,算数を必要とするだろうし,さらに改善の必要を見いだし,改善し続けていくであろう。
このように,こどもが,思考や行為を改善していくようにするにはどうしたらよいか。それには,こどもが,人類の進歩に尽してきた努力や,算数がはたしてきた貢献を知り,数量的な処理の方法を,具体的な生活をとおして理解し,さらに生活の処理に,これを適用する能力を伸ばすことが必要になるであろう。また,これと同時に,自己の生活を改善し,社会の進歩に協力する態度を伸ばしていくことも必要になるであろう。
2.算数と教育の一般目標
| 算数は,教育の一般目標を達成するのに,どのように役だつか。 |
算数の指導は,小学校教育全般の中で,どんな役割を果すのであろうか。どの教科も、それぞれの性格に従って,その目標を達成しようとするが,常に教育全般の目標を忘れずに,互に協力してこそ,教育の一般目標を達成することができるといえる。
本節では,教育の一般目標が,算数とどんな関係にあるかを述べてみよう。そうして,とれをとおして,教育の一般目標を達成するのに,算数はどのように役だつかも,明らかにしてみよう。
(1) 算数は,教育の−般目標とどのような関係にあるか。
(a) 一般編に示してある教育の一般目標は,社会の理想を示している。そうして,その社会の必要とその社会に生活しているこどもの必要とが結びついたねらいを示している
社会は,その理想に従って,こどもの生活に必要なものを選び,これをこどもの具体的な生活をとおして計画的に.能率的に指導しようとしている。そのために,こどもの本性を尊重しながら,こどもひとりひとりの行動や考え方の,望ましい方向を見いだし,その方向に修正し,新しい人間を形成して,社会を改善しようとするのである。このようなことをねらって書かれたものが,教育の一般目標である。
(b) 算数は,こどもの生活に有用なものである
こどもは,社会の歴史の中に生れてきたものである。しかも,その中で生きていこうとしている。その社会の中には,数が非常によく用いられている。これをうまく処理していくことができないようでは,社会で生きていくことができない。このような意味から,算数を用いないでは,こどもは,社会にうまく適合していくこともできず,また,うまく個人生活をしていくこともできない。
このように考えてくると,算数は,こどもにとって,きわめて有用なものであるといえる。言い換えると,こどもの個人生活にも,社会生活にも,数を用いることが必要になってくる。この必要にこたえられるように,数をうまく用いることができるようになると,それだけ,こどもは,社会における責任を果すことができるのである。
(c) 算数は,他の教科と,手をたずさえて,教育の一般目標を達成するのに欠くことのできない独自の目標をもっている
人間は,どんな生活をするにも,数量関係をうまく処理することが必要になる。しかも,その処理が科学的であり,技術的であり,能率的であることが,近代的な処理の一つの性格である。算数はこの性格を実現していくために,なくてはならないものである。
しかも算数は,本来,鋭い刃物のようなものであって,良い目的を達成するためにも,悪い目的を達成するためにも使われるものである。したがって,このように考えてくると,算数は,どこまでも,生活の改善向上のために使用する人間の善意と結びつけるようにしなければならない。そのためには,他の教科と手をたずさえて,常によりよい目的を実現するために使っていくように,指導されなければならないといえる。
このようなことが考慮されて,はじめて社会改善と個人生活の向上に対し,算数がすぐれた道具となることができ,教育の一般目標が達成されるのである。

(2) 算数は,個人生活をよりよいものにしていくのに,どのように役だつか。
個人生活を充実するには,日常生活に必要な,基礎的な知識・理解・能力・態度を身につけて,生活を改善していくために必要な問題を解決し,環境にはたらきかけていく能力を伸ばすことがたいせつである。
しかも,このようなことができるようになるためには,数えたり,計算したり,測ったりするようないわゆる,数量関係を処理する能力を伸ばすことがたいせつである。
算数が,数量的に物事を,正確に,的確に,能率的に処理する能力を伸ばすものであってみれば,個人生活を向上させる上にも,欠くことのできない重要なものである。
これを具体的に説明するために,一般編にあげてある,いくつかの項目について,算数がどんなに役だつかを述べてみよう。
(a) 物事を自主的に学ぼうとする意欲と,正しい態度を養うのに役だつ
たとえば,自分の計算の結果と,友だちの計算の結果とがちがっている場合に,この二つの計算をよく調べて,自分の計算がはっきりと誤りであることが認められないかぎり,他人の意見を受け入れるわけにはいかない。
算数は,判断の自主性を性格としてもっている。したがって,算数を用いると,自主的な判断ができやすい。
(b) 物事を正確に処理せずにはいられない,鋭い道徳的感情を養うのに役だつ
文明が進むにつれて,集団の成員の協カが必要になり,めいめいの行動や思考が,正確で能率的であることが,今までよりもいっそう重要なことになってきている。そのために,数量関係を処理していくときに,これを機械的にし,単純化して,できるだけ労力を節約することが必要になった。特に,最近,社会のどの機構も組織的で,計画的になり,しかも,数量的に運営されるようになってきている。したがって,その機構のうちのたれかが,不正確な処理をしたり,能率のあがらない方法を用いて処理したりすると,その影響は,機構全体に及んでくるのである。
このような点から考えると,不正確であったり,能率があがらなかったりすることは,簡単な金銭の支払いや,つり銭を渡すことに至るまで,近代社会では道徳的でないということができる。すなわち,もらうお金,支払うお金,おつりなどについての処理が正しくでき,しかも,その処理が速くできるということは,他人に迷惑をかけないという点から考えて必要欠くことのできないことである。したがって,計算が正しく,しかも速くできるようになることは,近代の社会における道徳的な感情のあらわれであるということができる。
算数で,よく売買についての経験を取り扱うことがある。これは.単に知識を得させるというだけではじゅうぶんであるといえない。正しく計算をしたり,正しく測定をしたり,また,適当な機会に,その正しい計算や測定をしないではいられない感情が,行為に表われるようになるまで指導することがたいせつである。
計算や測定は一般に,経済的な道徳的な感情をうらづけるもののうち,重要なものの一つである。したがって,計算や測定が,正しくしかも能率的にできるということが,道徳的感情を高めていく第一歩であるといえる。
数量を正確に,的確に,能率的に処理する方法や技術を指導するとともに,近代の生活が,数量的な判断を特に必要としていることについての指導もまた重要である。
このように考えてくると,算数科は,他教科と協力しながら,他人の不正確や非能率がなおざりにできないばかりか,進んで,正確に能率的に処理せずにはいられない道徳的感情を養う使命をもっているといえる。
したがって,算数は,鋭い道徳的感情の基礎を養うのに,役だてることができるといえる。
(c) 物事をはっきリ言い表わしたり,書き表わしたり,また,人の話を聞いたりするのに役だつ
物事を,筋道をたてて考えたり,それを,他人によくわかるように説明したり,また,他人の話を聞いて.その真意を正しく理解したりすることが,われわれの個人生活にとって重要なことであることは言うまでもない。
前節で述べたように,量の大きさをはっきり表わすために,人々は命数法や記数法,測定法などを考え出したのであった。また,表現を正確にするために,用語や記号をきめ,その意味内容もきっちりと決めたのである。
近代の社会では,いっさいのことが,正確に,的確に,能率的に処理されなければならないので,できるだけ,物事を数量的な角度から考察して,その内容を明らかにしようとしている。
物事を,数量的に筋道を立てて,はっきり考え,これを正確に,的確に,能率的に処理することは,算数のもっている本来の使命であるといえる。この意味から,算数は,物事をはっきり言い表わしたり,書き表わしたり,また,人の話を聞いて判断したりするのに役だつものであるといえる。
(3) 算数は,家庭生活および社会生活を,よりよいものにしていくのに,どのように役だつか。
こどもが,家庭や社会で生活するときに起ってくる問題を理解したり,処理したり,発展させたりしていく上に必要なものとして,いろいろなものをとりあげることができる。社会制度や組織についての理解,そこに起る問題を処理する能力,お互に個性を尊重したり協力したりして,家庭や社会の秩序を保持したり,社会を健全に発展させようとする努力,また,その一員としての責任を果そうとする努力などは,どれも重要なものである。
こうした家庭生活や社会生活の中には,その中から数量関係を見いだし,これを正確にとらえて,能率的に処理することの必要なものがある。これを具体的に説明するために,一般編にあげてある,いくつかの項目について,算数が,どんなに役だつかを述べてみよう。
(a) 家庭生活や社会生活を能率的に営むのに役だつ
家庭生活や社会生活に関係して,数量的処理を必要とする場合の多いことは,常に経験しているところである。
たとえば,家計について考えてみると,衣・食・住・文化……の費用,税などを計画的に処理することは,家計の根本であって,これがうまくいくか,いかないかは,仕事の能率に直接に関係してくるものである。また,仕事の計画を四季により,月により,日によってたてることも必要なことであって,これもまた,仕事の能率に直接に関係をもっているものであるといえる。
このように,家庭や社会に関係のある問題を,数的な資料を考察することによって,それを概括的につかみ,あるいは,正しく処理することによって,社会生活や家庭生活を能率的にしていくことができる。
(b) 家庭や社会の秩序を立てるのに役だつ
家庭や社会の秩序を立てるものとして,いろいろと考えられるが,時間や金銭の問題は,特にたいせつである。いかに他の条件がそなわっていても,経済的な面を抜きにしては,生活できない。また,時間的な計画を無視しては,やはり生活はうまくできない。この二つがうまく処理されて,はじめて,社会の秩序を保っていくことができるといえる。
また,家庭や社会の秩序のうらづけをしているものには信用があるが,これも,時間や金銭の正しい取扱に基くものであるといえる。
たとえば,時間についての処理が正しくできないために,約束の時刻が守れなかったとすれば,これによって,社会の秩序の基礎は乱れ,他人に迷惑をかけるばかりでなく,社会的な信用をおとすことになる。

算数では,金銭に関する計算や,金銭の処理に必要な,銀行の手続や売買の手続として,収支勘定,勘定書,領収書などについて,指導することになっている。また,時間については,時刻表,時間を使った計画のたて方などについても指導することになっている。これらはともに,前に述べた理由から,社会の秩序をささえる基盤のうちの重要なものの一つである。
(c) 有能な指導者,ものわかりのよい協力者となるのに役だつ
有能な指導者に必要な性格として,次のようなものを,あげることができる。
(ⅰ) 物事を概括して,全体的な見とおしをつけることができる。
(ⅱ) 物事を綿密に観察して,周到な計画をたてることができる。
(Ⅲ) 自主的に判断ができる。
(ⅳ) 判断の理由が,協力者によく理解されるようにすることができる。
たとえば,ある団体が,ハイキングに行くために,リーダーを選んだとしよう。リーダーは,目的地,道順,キロ程,時間,時刻,費用,団員の体力等を考慮して,計画をたてなければならない。そうして,これをみんなに示して,相談しなければならない。この際に,できるだけ,数量的な資料を示して自分たちの判断の根拠を明らかにするとともに,これを理解してもらうことが必要である。この場合に,示された側の者もまた,リーダーの判断の根拠を詳しく検討して,自分で納得のいくまで話し合ったり,必要に応じて,その計画を修正したりすべきである。
このように,リーダーも団員もともに,確かな資料を用い,その計画についてじゅうぶん納得し合わなかったら,団員全体の調和もとれないだろうし,建設的に,積極的に,お互に協力し合うこともできないであろう。
このように,確かな数的な資料をもとにして,自主的に物事を考えたり,自主的に他人の意見をとり入れたりするために,算数は重要なものであるといえる。
物事を数量的に精細に観察して処理することは,きわめて重要なことではあるが,不必要に精細に処理する必要はない。目的に応じたくわしさで,資料を処理することが重要である。これこそ,算数本来のねらいであるといえる。
このような意味から考えると,必要に応じて,物事を概括的にみることも,重要なことであるといえる。
概数をとったり,概算をしたりして,全体の見とおしをもつことができることは,うまく,物事の本質をつかみ,それをうまく表現して,利用する上に,たいせつなことである。
これもまた,指導者にも,協力者にも必要な能力ということができる。
(4) 算数は,経済生活および職業生活をよりよいものにしていくのに,どのように役だつか。
経済生活や職業生活を改善していくことは,わが国で最も重要なことの一つである。言い換えると,生産や消費の面において,数量関係をとらえ,これを正確に,的確に,しかも能率があるように処理することが要求されている。
たとえば,品物の計量,金銭の勘定,製品の規格の正しさ,期限の厳守などがそれである。
また,経済生活をじょうずに営むには,需給の様子や物価などを概観することが重要である。
このような数量関係を正しくとらえ,これを正確にしかも能率のあがるように処理する方法や態度を養うのに,算数を役だてることができる。
これを具体的に説明するために,一般編にあげてあるいくつかの項目について,算数科が,どんなに役だつかを述べてみよう。
(a) 経済生活に必要な知識を広くするのに役だつ
経済生活に関係した事がらのうちで,こどもが当面するものとして買い物・お使い・学校の費用・貯金・こども銀行などがある。また,間接的ではあるが,店の売上げ・損益・銀行・郵便局・税・予算など,多くの事がらに接する機会が考えられる。
算数科は社会科などと手をつないで,貨幣・金銭勘定・収支決算・勘定書・貯金のしかたなどの意味や取扱方について,指導しようとしている。このような点から,算数は,経済生活に必要な知識を広めるのに役だつものであるといえる。
(b) 経済生活を良心的に営む態度を伸ばすのに役だつ
算数では計算をしたら,これをいつも確かめるように導こうとしている。これらは,金銭勘定をしたり,個数を数えたり,測定したりするときに,なくてはならない心構えであり,いつも,やさしく確かめることができるように,処理する態度を伸ばしていくことが重要である。
測定をする場合に,計器が不正確であったのでは,何の役にもたたない。したがって,測定をする場合には,正しい計器を用いることが,まずたいせつである。また,計器の構造とはたらきについての知識をもち,計器を用いる場合には,必ず,計器のくるいの有無を確かめ,もし,くるっているようであったら,これを修正して用いるような態度が身についていることもたいせつである。
このような傾向を常に伸ばしていくと,売買するときに,正しい計器で測定しないではいられない気持を養うことができる。
お金の勘定を正確にすることは言うまでもなく,前に述べたように,品物の量を正しく測定することも,経済生活を良心的に営むための基本的な事がらである。
このような点から考えて,算数は,経済生活を良心的に営む態度を伸ばすのに役だつといえる。
(c) 予算を立てて,消費生活をご計画的に営むのに役立つ
こども個人の小づかいにしても学級会計にしても,予算を立てることが必要である。全体の収支の関係から,各費目の支出予定を考えるには,算数は欠くことのできないものであるといえる。また,学校の運動部,図書部,新聞部,科学部などの各部が,月々,どんな支出を必要とするか,また,どれだけの支出を必要とするかなどについての計画が考慮されていなかったら,これらの各部の運営を,うまくしていくことはできない。
また,帳簿の記載,収支計算などを正確にしておかなかったら,帳簿の上の金高と,現金とが,きちんとあわないだろう。これでは,帳簿を消費生活に役立てていくことにはならない。
したがって,算数は,前に述べたようなことが起らぬように,予算をたて,消費生活を計画的に営むようにしていくのに役立つといえる。
こ の 節 の む す び
算数が,教育の一般目標に対して,どのように役だつかについて述べてきた。
算数は,生活の各分野を,数量的な立場から考察し,これを,正確に,的確に,能率的に処理するためのものであり,個人生活とともに,社会全般の改善向上をはかることをねらっている。
すなわち,算数は,数量関係をうまく処理するための,すぐれた道具であるばかりでなく,物の見方や考え方を伸ばしてくれるものでもある。しかし,これは,算数科だけでできることではなく,他教科との関連協力によって,はじめて,できることである。教育の一般目標を達成することも,このようにしてはじめてできるといえる。
われわれは,算数をじゅうぶん使いこなせるようにするとともに,これを善用して,個人生活の向上はいうまでもなく,人類の進歩と社会正義のために貢献していこうとする態度を伸ばさなければならない。この後者の望ましい態度が伸ばされて,はじめて,算数は,社会において役だつものであるということがいえることを忘れてはならない。
3.算数科の一般目標
| 算数科の一般目標として,どんなものが考えられるか。 |
第1節では,算数が,われわれの生活に有用であるとともに,こどもの必要にこたえるものであることを述べた。
第2節では,教育は,社会の理想を実現して,人類の進歩をはかるための,重要な社会機能であること,算数はその中にあって,教育に欠くことのできないものであること,伸びようとするこどもの数量的な必要を満たすものであることなどを,個人・社会・経済の生活の面から述べた。
本節では,前の二つの節を受けて,算数科の一般目標の意義とその内容について述べよう。
(1) 算数科の一般目標は,どんな意義をもっているか。
教育が,社会の理想を実現するために企画されるものであるから,その理想は,どんなところにあるかを,めいりょうに示さなければならない。これが何であるかを示したものが,教育基本法にある教育の目的であり,一般編にある教育の一般目標である。
さて,これらの教育の目的や教育の一般目標を実現しようとして,こどもの具体的な生活を分析したり,おとなの社会生活を考察したりして,それらの生活に必要なのものの中から,数量的な処理に関するものをとりだし,これを,こどもの成長発達を考慮してまとめたものが算数科である。
算数科は,教育の一般目標の中で,主として,どんな分野を担当しているか,また,その学習は,どんな点をねらいとして進めたらよいかを示したものが,算数科の一般目標である。
次に,その内容を述べてみよう。
(2) 算数科の一般目標として,どんなものをあげることができるか。
(1) 算数を,学校内外の社会生活において,有効に用いるのに役だつ,豊かな経験を持たせるとともに,物事を,数量関係から見て,考察処理する能力を伸ばし,算数を用いて,めいめいの思考や行為を改善し続けてやまない傾向を伸ばす。
(a) 一般社会人の生活,特に経済生活をしていくのに必要な数的資料として,どんな種類のものがあるか,また,これをどこから手に入れることができるかなどの知識を広めるとともに,その資料を利用する能力や傾向を伸ばす。
(b) 日常生活を,数量関係から見て分析したり,総合したりして,筋道をたて,問題をとらえる能力や傾向を伸ばすとともに,これを解決する能力を伸ばす。
(c) 社会・理科・図画工作などの算数以外の分野において,数量関係を見抜き,それが,巧みに処理できることから,算数が,どんなに大きな貢献をしているかを知り,数量関係を生かして用いる能力や傾向を伸ばす。
(d) 書物を読んだり,実務を処理したりするときに,よく出会う数量関係についての用語や記号の理解を深めるとともに,これらの用語や記号を用いて,正しく考えたり,まちがいなく他人に伝えたりする能力や傾向を伸ばす。
(e) もののねうち,長さなどの測定の発達,その測定の社会的意義,実測の手続についての理解を深め,計器の使用に必要な技能を伸ばすとともに,正確な計器を正しく用いる能力や傾向を伸ばす。
(f) 算数は,数量関係をいっそう正確に,気楽に,能率のあがるように,しかも的確に考察処理するのに有用であることの理解を伸ばすとともに,算数を生活の向上に生かして用いる能力や傾向を伸ばす。
(2) 数学的な内容についての理解を伸ばし,これを用いて数量関係を考察または処理する能力を伸ばすとともに,さらに,数量関係をいっそう手ぎわよく処理しようとして,くふうする傾向を伸ばす。
(a) 位取りの原理についての理解を探め,これが,計算や記録するのに,簡単で能率をあげるのに役だつことの理解を深める。
(b) 必要に応じて,正しく,しかも,適当な速さで計算ができるようにする。
(c) 必要に応じて概数をとったり,概算をしたり,また,近似値を用いる能力を伸ばすとともに,その正確さと,それに対する制約についての理解を深める。
(d) 数量的な用語や記号についての理解を伸ばすとともに,これを正しく用いる能力を伸ばす。
(e) 数量関係をはっきり示すためにいろいろな方法を用いたり,その方法をくふうしたりする能力を伸ばす。
(f) 図形の性質や物の形の概略を,直観的にとらえる能力を伸ばすとともに,物の形や構造を,図やことばで表わしたり,模型に作ったりする能力を伸ばす。
(g) 数的な資料を,表やグラフにまとめたり,表やグラフで示されたことを理解したりする能力を伸ばすとともに,表やグラフを有効に用いる能力を伸ばす。
(h) 数量関係を,いっそう手ぎわよく考察処理しようとして,くふうし続ける傾向を伸ばす。
こ の 章 の ま と め
この章は,算数とわれわれの生活,および算数と教育の一般目標の二つの面を考察し,これに基いて,算数科の一般目標をあ明らかにした。これを要約すると,次のようになる。
(1) 算数とわれわれの生活
(1) 人類は,生活の必要から,個数を数える方法や数を記録する方法を進歩させてきた。
(2) 十進数の原理が使われるようになって,どんな大きな個数でも,簡単に数えることができるようになった。
(3) 十進法による記数法が使われるようになって,簡単に数を記録したり,簡単に数の大きさを比べたりすることができるようになった。
(4) 十進法による数え方や記録の方法は,数を他人に伝えるのに便利である。
(5) 十進法による記数法は簡単なので,計算もそれによって簡単にできる。
(6) 計算を用いると,数えるという肉体的精神的な労力を節約することができる。
(7) 社会で使われる測定の単位が統一されているので,この単位を用いると,他人に正しく量の大きさを伝えることができる。
(8) 生活の必要から,いろいろな測定器具が発明されてきたので,それを用いると,手軽にしかも詳しく量の大きさを知ることができるようになった。
(9) 図形を用いると,物の形や構造をやさしく他人に伝えることができる。
(10) 図形は,自分の考えを進める上に有用なものである。
(11) 用語や記号は,記録したり,考えを整理したり,また,物事を他人に伝えたりするのに簡単で便利である。
(2) 算数と教育の一般目標
(1) 教育の一般目標は,新しい人間の形成と,それによって社会を改善していくところにある。
(2) 算数を用いないでは,日常生活をうまくして,社会に適合していくことができない。
(3) 算数は,その処理の性格が科学的であり,技術的であり,能率的である,また,この性格を,こどもたちに明らかにすることがたいせつである。
(4) 算数は,自主的に学習しようとする態度を養うのに役だつ。
(5) 算数的処理をとおして,鋭い道徳的感情を養うことが必要である。
(6) 算数は,家庭生活や社会生活を計画的にしかも能率的にするのに大いに役だつものである。
(7) 算数は,社会のきまりを正しくするのに役だつものである。
(8) 算数は,経済的な生活に必要な知識を広めたり,生活を良心的に営む態度を伸ばしたりするのに役だつものである。
(9) 予算を立てて,消費生活を計画的に営むのに役だつものである。
(3) 算数科の一般目標
(1) 生活に起る問題を,必要に応じて,自由自在に解決できる能力を伸ばすことがたいせつである。
(2) 数量的処理をとおして,いつも生活をよりよいものにしていこうとする態度を身につけることがたいせつである。
(3) 数学的な内容についての理解を成立させないと,数量を日常生活にうまく使っていくことができない。
(4) 数量的な内容についてのよさを明らかにすることがたいせつである。
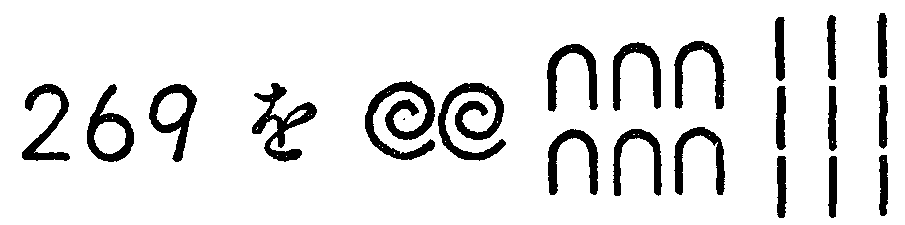
![]() が10個で
が10個で![]() (10),
(10),![]() が10個で
が10個で![]() (100)と決めて書き表わしているのである。
(100)と決めて書き表わしているのである。