①　学習段階に応じて，教材を選択すること　②　概略の形・大きさを用いること。　③　対応観念を用いること。　④　各種の数の意味を明らかにすること。　⑤　くりかえし練習を積むこと。　⑥　四則算法の意味を明らかにすること。　⑦　四則算法の間にある関係を明らかにすること。　⑧　計算過程の合理化をはかること。　⑨　計算において，よりよい方法を用いること。　⑩　力の意味を明らかにすること。　⑪極限の観念を明らかにすること。

①　学習段階に応じて，教材を選択すること

　子供は最も簡単かつ具体的な経験をもとにして生活している。しかし，子供は自分の自然な成長に促がされて，いつまでも同じような生活にとどまっていられない。教育は，この子供の欲求してくる機会をとらえて，熟練した人が行うような抽象的な思考過程に至らせるものであるといえる。したがって，学習は教育者がなかだちになって，生徒が自分の力で切り開いていく個人の進歩であると考えられる。

（一）　教師は教材としての素材を，子供の生活環境から採るように心掛けねばならない。

　しかし、生活環境といっても，子供の直接に経験することだけに限定せず，社会人として当然関心を持っているものや，関心を持たねばならないものをも含めて考えてよい。

　このようにして始めて，より広くより深く環境に対して，数理を用いるようになるのである。

（二）　抽象的な過程に至るといっても，一挙に最後の段階に達し得るものではなく，そこには種々の段階がある。しかもこの段階は，くりかえし練習しなくても，一つの段階から次の段階に移り得るように，きわめて自然的な発展過程として，くみたてられなくてはならない。

②　概略の形・大きさを用いること

　具体的な経験から素材を選んで，それを数や言葉で表現する場合に，表現されたものはどこまでも，概略の大きさや形に止まるものであるといってよい。

　これが有効な表現として人間生活に意味を持つのは，目的に達するような精度において表現されているからであるといえる。そこに数学における正確度ということと，その制約が問題となるのである。

（一）　統計に現われる数値を，測定によって得られる数値に関係をもたせて，有効数字に関する観念を明らかにしなければならない。一つの物の体積を測ろうとする場合でも，測定に用いる物指の最小目盛が１センチか１ミリか1/20ミリか1/100ミリかによって，測定値をどこまで信用してよいかが定まるわけである。面積や体積等を計算する場合に，測定値の有効数字が幾けたまでであるかを念頭におかないと，徒らに無意味な複雑な計算をして，不必要な労力を使ったり，また目的に応じて物指の精度を吟味したりする手段を忘れるものである。

（二）　測定や計算にとりかかる前に，その結果を予想してかかることは，計算過程を簡略にしたり，計算に於ける誤りを発見する有力な手段である。

（三）　概数をとる場合でも，切り捨て，切上げをするよりは，四捨五入をする方が，より正確な結果が得られる。二捨三入すれば，より一層正確な結果が得られる。切り捨て，切り上げが10単位として切り捨て，切り上げをするものであるとすれば，四捨五入は５を単位としてするものだからである。また，概数について計算する場合には，目的に応じて方法が選ばれなければならぬ。

（四）　形を取り扱う場合においても，概形に留意することが大切である。実際の取り扱いに際しては，種々の具体的な物の中から，共通する概形をとらえさせ，これから幾何学的な言葉によって定まっている形の概念，例えば正方形，矩形にまで発展させるべきである。これと逆に幾何学的な言葉によって定まったものとして形を先きに与えようとし，自然物をこれにあてはめてみるような指導に陥ってはならない。もし，このような指導を行うならば，子供は徒らに自然物を不完全なものと考えすぎたり，言葉を具体物に適用する自信を失うからである。このようなことでは具体的な物の形（これを言葉で言い表わせば，概形しかつかむことができないかもしれないが）と理想化された表現を理解し得ないものである。

③　対応観念を用いること

　算数は，日常の色々な現象を数や量や形に関係して調べていくものであるが，量は数に対応させて処理していくことができる。故に，処理するということを考えるには対応させる能力は欠くことのできないものである。この能力を養う留意点を二三述べてみよう。

（一）　数に対応させるには，その予備段階として，事柄を整理したり分類したりすることの指導が大切である。

　例えば，数える場合には，まず，何を数えるかを明らかにし，次に，どんな順序で数えるかを考えて，その物の整理，分類ということが行われねばならない。自動車を数える場合でも，単に自動車は何台かという場合と，乗合自動車は何台か，貨物自動車は何台かという場合とは，数える対象や数える操作が違ってくるのである。

（二）　次に，何を単位として数を対応させるかを明らかにしなければならない。

　普通に個数を勘定するように，１つを１つとして数えていくか，あるいは１つを1/10，1/100，等を単位として数えるか，あるいは単位分数を単位として表わしていくかは，場合によって異なる。

　量の場合でも，長さは何を単位とし，広さは何を単位とするか，また，かさは何を単位として表わすかを定めなくてはならない。このように，数との対応を考える場合に，まず，単位を決定することが大切である。

（三）　次に，対応については，one　to　one，one　to　many，many　to　one，many　to　manyの四つの仕方が考えられる。

　one　to　oneというのは，上に述べたように単位を定めて，それに対して１を対応させる仕方である。これによっては何も新しい数え方が生まれてこない。

　many　to　oneは，多くのものに対して１を対応させる仕方である。例えば，２,３,４等の基数を１に対応させる掛算九九の数え方や10,100,1000を単位として数えるものである。後者は，数の位取りを明確にすると同時に，多くのものを数える時における大切な数え方の—つである。

　one　to　manyは１つのものを，都合によって幾つかのものとして考えていく対応のさせ方である。分数や小数を単位として数えていくのがこれである。

　小数や分数は，ただ単に端数を処理するという便宜的なものではなく，数を適切に取り扱っていく技術に関係するものであるといえる。

　many　to　manyは多くのものに対して多くのものを対応させていく仕方である。これは比の考えにつながるものであり，複雑な量を簡潔に表わすためにも用いられる。

④　各種の数の意味を明らかにすること

　数は，数学史によって明らかな如く，正の整数が基となって，次第に発展したものである。これをいろいろの立場から考察することによって，いろいろな数のはたらきというものを，次第にわからせることができる。次にその二三の立場を示してみよう。

（一）　数の形の上からの系統

　整数は１,10,100,1000‥‥を単位として，物の大きさを表わすものであるといえる。即ち，１，１の10倍，更に10倍というように単位の系列として１から次第に大きいものを作り，これを用いていく数え方である。

　これに対して１,0.1,0.01,0.001，等を単位として，物の大きさを表わしていく仕方も考えられる。これが小数である。

　しかしこのようにして生れた小数も，単に形式的なものに止めてはならない。できれば，計算を簡単にするため，単位を適当にかえて，小数で表わしていくことが考えられなければならない。このようにしてはじめて，小数は小数として，はたらきを持つものとなるのである。

　また，１を10,100,1000‥‥等に限らないで，任意の整数で割ったものを単位として表わしていく仕方も考えられる。これが分数である。したがって，小数は幾つかの特殊な分数を単位として表わしたもので，諸等数であるとも考えられる。

　よって，小数計算では，普通の諸等数と同様に，単位をそろえて加減するように指導すればよいわけである。また，分数についても，単位が違っている時に，共通な単位を見出して，それを用いて計算が進められなけれはならない。

　このように，数や量に関する計算が，一つの統一された考えのもとに行われるということが，数や量，あるいはその関係の理解を一層深める所以である。

（二）　数計算の上からの系統

　数計算を行う時に，その結果ができるだけ簡潔に表現できるようにしたいということは誰でも考えることである。この立場から，数の系統を考えてみよう。

　減法が被減数・減数の大きさの如何に関孫なく，できるようにするためには，負の数を導入する必要がある。

　かくして導入された負の数は，そのような抽象的な働きのみに限らないで，ある場合には方向のある量を表わしたり，あるいははたら準点を設けて，そこを基準としての増減を表わす時にも用いられる。

　また，除法で割り切れない時に，それを簡潔に表現するのに分数がある。また，小数も使うことができる。

　一般に小数を用いれば，分数よりも，その大きさの観念が明確となり，分数を用いれば大きさが正確に表われるものである。したがって，計算の途中においては，分数を用いて正確度を保つことに心掛け，大きさを明確に表わす必要のある時に，はじめて小数を用いるように心掛けることが必要である。

　整数に関する乗除計算で，その結果に正確度を要求していくときには，これを分数の形に書き直して分母分子を計算し，まず，答を分数で出し，次に，これを小数で表わすようにするがよい。

　また，平方する計算の逆計算として，平方根を求める計算が考えられる。この結果は，小数ではっきり表わすことのできないのが普通である。ここで平方根数を導入して，それを記号で表わしていく方法が生れてくる。

　もしもこれを忘れて，単なる形式計算に終始するならば，数が十分理解されないばかりでなく，社会において十分に活用されずにすんでしまうであろう。

⑤　くりかえし練習を積むこと

　くりかえし練習を積むことは，具体的な処理において，計算が子供にとって精神的な抵抗にならないようにするためである。

　ここで精神的な抵抗にならないというのは，計算処理の過程において，論理の段階に支障を起さず，更に大略を見透すことができるだけの，精神的なゆとりが生まれてくるような状態にあることを意味する。

　くかえし練習をする際に，次の二つの点に留意すべきである。

（一）　くりかえし練習する計算の対象は，計算能力を考える場合の根本的なものであり，また，計算方法の一段階となるようなものであることが必要である。

　子供が少し考えれば，すぐ次のより高い段階に考え及ぶようなことは，練習を重ねても，低い段階の方法を固定させることになって，かえって，よりよい方法を習得させる場合の障害となり，教育的にも決して有益なものではない。

　例えば珠算を指導する場合に，五珠の特殊性を活かして，加減法を導入しても，計算の仕方を考えていく順序が必ずしも珠をうごかすのに便利であるとはいえない。このような場合に，前者の方法によって，加減をくりかえし練習することは無意味である。また，正方形・矩形の面積を計算する方法について指導する場合に，まず，小さないくつかの正方形に区切りその個数を計算する方法もあるが，これは容易に縦・横をかけて計算する方法に発展し得るものである。この場合に，前者の方法によってくりかえし練習することも無意味なことである。

　要するに，くりかえし練習を行う対象となるものは，形式として固定されるに値するものであって，かつ，次の段階に到達するために，相当の智能が要求されるものでなければならない。

（二）　形式は，もともと一定のものではなく，次の段階における形式の中にとけこんでいくのでなければならない。即ち，形式は何時になっても固定しているものではなく，次第により高い形式へと発展していくべきものである。例えば筆算の乗法において，被乗数と乗数との部分積が単に一けたずつずれるという機械的形式に固定しないで，部分積をかける数字の位置の真下から書くような形式にまで高めるがよい。この形式は，やがて乗数の数字に０を含んだ場合における，簡便算にまで発展するものである。

　このように，一つの形式は，その段階の計算を徹底させるだけのものとしてではなく，次の段階へと発展していく頭のはたらきの母胎として，役立つものでなくてはならない。故に，一定の形式を伴った技能は，智能の程度によって定まるのであって，智能に無関係に行わるべきものではない。

　技能は，いうまでもなくある一定の主題下において，くりかえし練習されなければならない。しかし，突差の際にも形式を用いて計算するまでに，技能が身についていなければならない。このような考えからも，一定の主題下になくて，くりかえし練習する機会を与えるようにしなくてはならない。指導においては，とくに後者に対する留意が大切である。

⑥　四則算法の意味を明らかにすること

　加減乗除は，社会に於ける各種の問題を，数・量・形について処理をする場合におけ最も基本的でかつ簡単な方法である。

　加法は“全部でいくつになるか”“全体はいくらか”という形の質問に対して行われるものである。即ち，一群のものがある時それに他の群を添加する場合か，あるいは二群の物が同時に存在するときに，その二群の物を一つの群にまとめる場合に用いられる計算である。

　減法は一つの数を持つていて，その一部分を知っているとき，他の部分を知る場合に用いられる計算であるといえる。実際指導においては，“幾つ残っているか”“幾つなくなっているか”“その差はいくつか”“もう幾つ必要か”の四つの質問の形式によって表わされる。しかし，いずれにしても，引算は一つの群が考えられたとき，その一部分がわかっていて，他の部分を一つの群にまとめる場合に，その群を数で表わすことであるといえる。

　乗法は加法と同じような形式で提出された質問に対して行われる計算である。つまり，同じ数を繰返して加える場合に加法または乗法が用いられ，等しくない数を加える場合には加法が用いられる。

　除法は次のような形式の質問に対して行われる計算である。即ち，一つの数が他の一つの数を何回含んでいるか，“一つの数を幾つかずつに分けたとき，その分けられた各部分は幾らか”の二つの形式である。

　第一の場合は，二つの群が与えられたとき，その一方が他一方と同等な群を幾つ含むかを計算するためのものである。これを包含除という。第二の場合は，一つの群を与えられた幾つかの同等な群に分解するためのものである。これを等分除という。いずれの場合でも，一つの群をいくつかの同等な群に再構成するのである。

　以上四つの算法は，互いに関係をもっているものであるが，また，独自な立場を特つことを，実際指導に即して，明らかにすべきである。

⑦　四則算法の間にある関係を明らかにすること

　四則算法の間にある関係を理解させるには，加法と減法，乗法と除法，加法と乗法，減法と除法というように，二つずつを組にして考えるがよい。

（一）　加法と減法

　加法・減法は，反対の操作を示すものである。即ち，加法は一つにまとめることであり，減法は一つの群から，その一部である群を取り去ること即ち，二つに分けることを意味する。





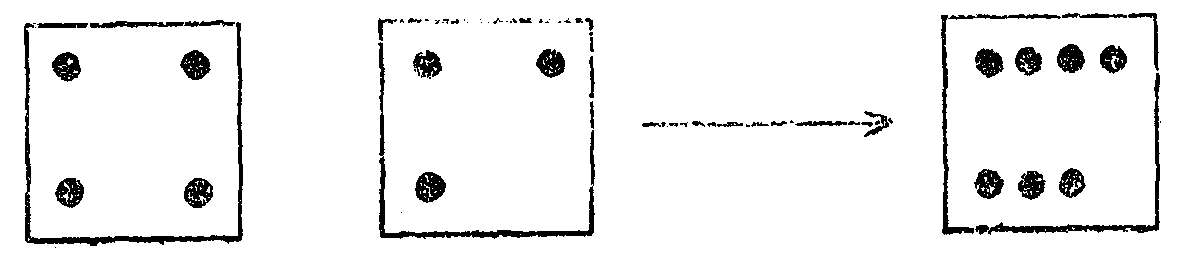
（二）　乗法と除法

　乗法と除法も，反対の操作を示すものである。乗法はいくつかの群を一つの群にするものである。また，除法は群全体を幾つかの同等の群に分けるか，あるいは与えられ個数だけの同等な群に分けることである。



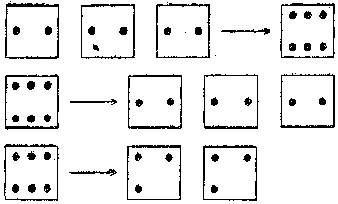
　なお，乗法の始めの導入では，倍とか割るとかいう言葉を用いないがよい。即ち，４×３を４つが３つずつで幾らかと読ませるがよい。また，12÷３を12の中に３は幾つあるか，あるいは12を同じように３つに分けると幾つになるかなどと読ませるがよい。このようにして，ある程度意味内容がはっきりわかってから，倍とか割るとかという言葉へもっていくように指導するがよい。

（三）　加法と乗法

　加法と乗法とは，幾つかの群を一つの群にまとめることである。同等であるか同等でないかによって，加法または乗法が適用されるのである。



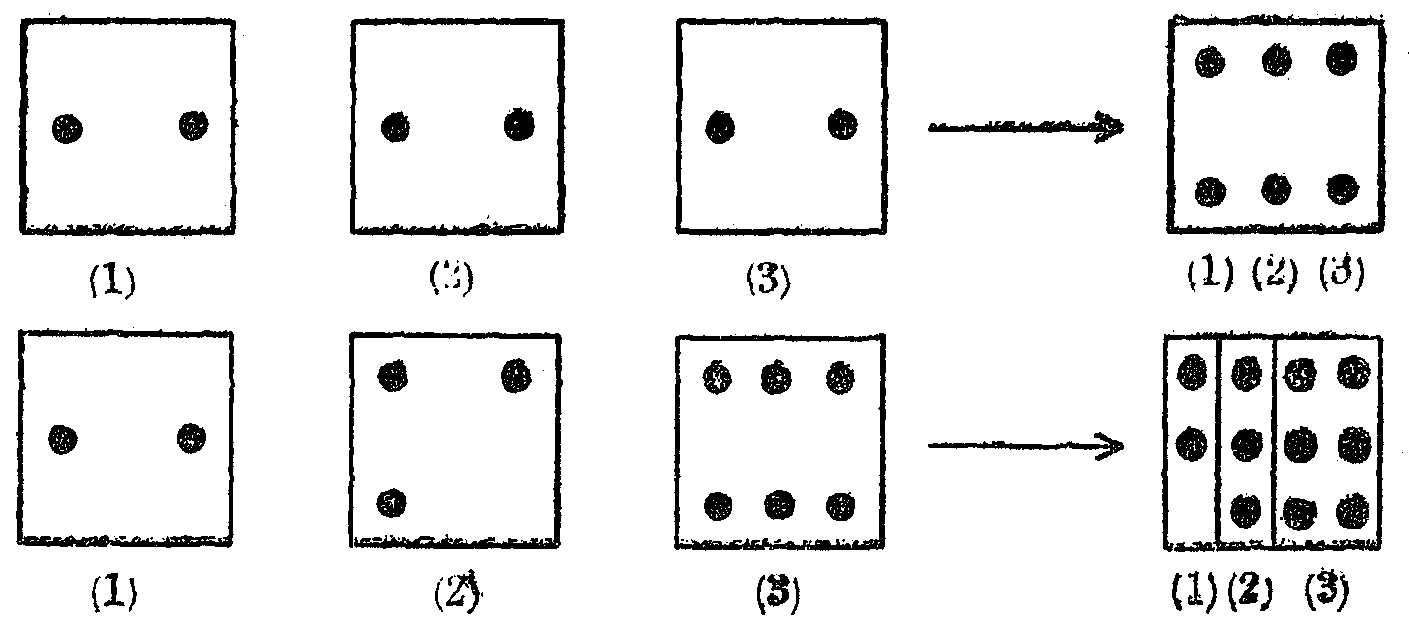
（四）　減法と除法

　除法は減法を連続的に行うためのものであるとみられる。

⑧　計算過程の合理化をはかること

　計算過程の合理化ということは，各種の算法についていえることである。ここにその大要をしるしてみよう。

（一）　暗　算

　暗算とは，計算過程を全く意識することなく，反射的に結果を得ることをいう。したがって，計算過程を意識するような計算は，外見上暗算のように見えても筆算と考えてよい。暗算と筆算は，紙の上に書くとか書かないとかいう形式上から区別されるものではなく，頭のはたらきの上から区別されるものである。また，暗算の範囲は一定しているものではなく，筆算・珠算などの計算能力が高まるにつれて漸次広くなっていくものである。いわば，子供の能力に応じて広くなっていくものである。

　暗算は形式上聴暗算と視暗算とに分けることができるが，小学校における聴暗算は，最も簡単なものとして，基数に関する加減乗除に限られるであろう。漸次その範囲を拡大して，加数だけが基数である場合，減数だけが基数である場合にも及ぶであろうと考えられる。しかし，これも子供の能力によって決定されるものである。

　視暗算は，数が目の前にあるもので，聴暗算と比べて容易である。この範囲も聴暗算と大体同様であると考えられる。しかし，方法として幾らかの違いは考えられる。

　例えば，37＋８を視暗算で行う場合に，７と８とをみ，加えて10以上になることから，直ちに，40以上として，まず十の位を４と定め，次に７と８とを加えた15の５を４の次の位に書き加えるがよい。

　また，45−８では，５と８とをみて，一位の数同志で引くことができないことがわかると，直ちに十の位を３と定め，次に，15−８を７として十の位の数字３の次の位に７と書きそえるがよい。

　87−68のような計算は，87−60−８とし，27−８と考えた上で，上と同様にできる。また，87−67−１とし20−１として考えることもできる。この場合，後者は前者よりも容易である。

　また，83−69のような計算は，83−70＋１として，13＋１と考えて計算することもできる。

　要は場合に応じて，適当な計算方法を案出するように工夫させ，程度の高い技能を身につけさせることが大切である。

（二）　珠　算

　珠算はその構造上の理由から，５を単位として計算を行なうものである。しかし，数の記法が10を単位としている関係から，５と10との補数関係を用いなければならない。

　例えは，12＋２または17＋２の計算では，一珠で２を入れることができるから，その計算は容易である。しかし，12＋３，12＋４，あるいは17＋３，17＋４では一珠でそれぞれ３，４を入れることができない。この場合には，３あるいは４の５に対する補数を一珠で払って，五珠を入れようとする。もし，五珠が既にはいっている場合には，それを払って十の位に一珠を入れればよい。また，五珠がはいっていない場合には，そのまま五珠を入れればよい。

　14＋８，14＋９のように，５以上の数を加えるとき、一珠で３あるいは４がはいらないときは３，４の５に対する補数を一珠で払う。払った数がそれぞれ，８，９，の10に対する補数であったことから，十の位に一珠を入れる。

　即ち，加法では５以下の数を加えるときは，一珠でそのまま加えるか，または５に対する補数を引き去って，五珠を入れることが基本となるから導入に際しては常に一珠に着目するようにしつければよい。

　また，５以上の数を加える時は，ます，その数ａから５を引いたもの，即ちｂ＝ａ−５が一珠ではいる時はそのまま入れ，次に，残りの五珠を入れるようにする。またｂ＝ａ−５が一珠ではいるが，五珠がはいらない場合は，五珠を払って，上のけたに１を入れる。また，ｂ＝ａ−５が一珠ではいらない時は，ｂの５に対する補数を一珠で払って，次のけたに一珠を入れる。

　しかしこの場合に，12＋３の如くに，思考の順序が，従来の運珠の順序に一致しない場合がある。このような場合に，形式を固定させないでよよい方法を考えさせ，便利な従来の運珠に気がついてから，くかえし練習を行うよう指導すべきである。

　減法についても同様で，被減数が５以下の場合には，それを一珠で引くことのできないときは，その数ａの５に対する補数を入れて，五珠があればそれを払えばよい。また，五珠がない場合には，上のけたの一珠を払って，下のけたに五珠を入れる。

　被減数ａが５以上の場合については，ａ＝５＋ｂとして、ｂが一珠で引けるときは，それを一珠で払い，五珠がはいっていればそれを払う。もし，五珠がはいっていないときには，上の桁の一珠を払って，今のけたに五珠を入れる。

　また，ｂが引けない時には，ｂの５に対する補数を一珠で入れ，上のけたの一珠を払えばよい。

　乗法は筆算の形式をそのままに運珠すればよい。この場合に位取りが問題となるが，それは概算で行えばよい。除法についても同様である。

（三）　筆　算

　筆算は計算の方法としては，最もよく行われるものである。場合に応じて他の方法によって計算させ，筆算のみにたよらないがよい。計算の原理は，算式が紙上に書いてあるために，いろいろと便宜な方法が考えられる。

　１．加　法

　筆算による加法は尾加法による。末位から加えていく方法である。この際に位取りをそろえるとか単位をそろえることが最も大切である。
 

125 +27

1.25 ＋0.27

１時　25分 ＋　　27分

　これが十分でないと，小数計算で間違いを起こすことになる。また，繰上がる時は，単位が何であるかを考えていくべきである。例えば下の計算で，分の単位から時の単位に移るには，60を単位としていかなければならぬことを注意するがよい。

１時　　37分
　　　　48分
１　　　85(60)
１　　　60
２　　　25
　

　これは整数，小数についての計算では形式的になりがちであり，それでも間違いは少ない。しかし，不十進諸等数になると単位についての概念が十分でないと，計算ができなくなる。同じようなことが，分数の加法についても，いえることである。

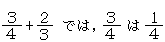　を単位として３であり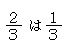，を単位として２であると考えられる。したがって，これを加えるためには，単位をそろえなければならない。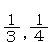を測ることのできる共通な単位は，明らかに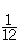である。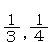はそれぞれ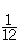を単位とすれば，４と３である。したがって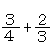，は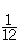を単位として17となる。よって

である。この分数計算では，単位は次のようなものである。
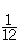，１，10，100，…
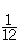を単位とするところでは，12を一束にして次の位である整数に移るのである。17−12＝５として，１を単位として１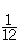，を単位として５であることがわかる。
　上の計算を，時間などの不十進諸等数等に関する計算についてのものと比べて，その考え方の同じであることに注意すべきである。

　２．減　法

　減法においても，加法と同じように，位取りをそろえるとか，単位をそろえることが大切である。
 

12 −7

1.2 −0.7

１時　２分 ＋　　７分

上の三つの計算は，同じ考え方で行うことができる。下の位で２から７を引くことができない時は，その上の単位のところから１だけをかりてくる。即ち，数の場合には，その単位を基にして測って，10をかりてくる。また，時間の場合には分を単位として60をかりてくる。その算法を式に書き表わすと

12−７＝（10−７）＋２

1.2−0.7＝（１−0.7）＋0.2

１時２分−７分＝（60分−７分）＋２分

というようになる。また分数についても同様である。例えば，



　上の計算で，分数部分同志だけで引くことができなくて，整数部分からかりてくることは，今までに述べたことと同じである。

　３．乗　法

　乗法においても，単位についての概念が，しっかりつかまれていなければならない。
 

147 ×7

1.47 ×　7

１時　47分 ＋　　７分

　上の三つの計算は，同じ考え方で行うことができる。

147×７では，次のような考え方になる。
 

100を単位としたところ	１×７＝７
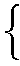
10を単位としたところ	４×７＝28		100を単位として 10を単位として		２ ８
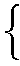
１を単位としたところ	７×７＝49		10を単位として １を単位として		４ ９
合わせて	100を単位として	７＋２＝９
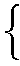
	10を単位として	８＋４＝12		100を単位として 10を単位として	１ ２
	１を単位として	９
更に合わせて	100を単位として	９＋１＝10	｛1000を単位として１
	10を単位として	２
	1を単位として	９
したがって	1000を単位として	１
	100を単位として	０
	10を単位として	２
	1を単位として	９

このようにして答1029を得るまでには上のけたから計算すると，何度も各けたの数字を補正していかなくてはならない。この不便を除くためには下のけたから数字をきめていくがよい。即ち，
 

１を単位として７×７＝49		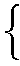10を単位として４ １を単位として９		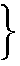	１を単位として９ 10を単位として12 100を単位として２
10を単位として４×７＝28		100を単位として２ 10を単位として８

100を単位として１×７＝７				100を単位として７‥‥‥‥‥‥‥‥‥‥
→		１を単位として 10を単位として 100を単位として	９ ２ 10		→		１を単位として 10を単位として 100を単位として 1000を単位として	９ ２ ０ １

　1.47×７でも，上のように考えることができる。しかし，このときは次のように考えてもよい。

　即ち，0.01を単位として，1.47を表わすと，147であるから

47×７＝1029
したがって　1.47×７＝10.29

　１時47分×７も同じように考えることができよう。即ち
 

時を単位として　１×７＝７
分を単位として47×７＝329		時を単位として　５ 分を単位として　29		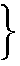→	時を単位として12 分を単位として29

　また，これを次のように考えることもできる。

　１時47分を分を単位として表わせば107分である。故に，１時７分×７を，分を単位として計算すれば，107×７＝749となり749分となる。
 

60)749(12 　　60 　 149 　 120 　　29

１時　47分 ×　　　７ 　７　329　60 　５　300　 　12　 29

　即ち，12時29分となる。

　次に，乗法における計算形式について考えてみる。

　　42×23で　42×３＝126　42×20＝840
 

となるから右の計算を得る。この場合に，840の終りのけたにある０は，部分積を書いていく位置をきめておけば不要であることに気ずかせることができる。	42 ×23 126 840 966
このように指導しておけば，42×203のような計算を考えさせる時，右のような筆算形式を生むであろう。	42 ×203 　126 84 8526

　このようなことを考えさせることによって，部分積を書く位置をはっきりつかまなくてはならない必要にせまられるであろうし，教師の指導も徹底するのである。

　次に，整数に小数をかける計算について考えてみよう。

128×5.2について考えてみるに

128×5.2と128×52とを比べると，かける数が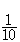であるから，前者の積は後者の積の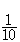である。したがって，次のような計算の仕方が考えられる。
 

1.28 ×52 256 640 66.56

128 ×5.2 　256 640 6.656

　
 

小数に小数をかける場合も同様であって，例えば1.28×52について考えれば，1.28×5.2は1.28×52と比べてである。したがって，右のように，計算することができる。 　分数に整数をかける計算においては，次のように考えることができる。即ち，×３では，はの４倍であるから×３は，の４倍を更に３倍することである。したがって，積はの12倍となる。

1.28 ×　52 　256 　640 66.56

1.28 × 5.2　 　 256 　640　 6.656

また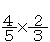，は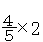と比べてかける数が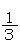である。したがって
４．除　法

　除法でも，乗法の時と同じように，単位の概念をはっきりさせておくことが大切である。

　84÷２で，84は10を単位としたものが８と，１を単位としたものが４である。したがって，84を２で割れば
 

84÷２

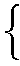10を単位としたもの　　４ １を単位としたもの　　２

したがって，　84÷２＝42　となる。

また，138÷２　では
 

138		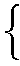10を単位としたもの　13 １を単位としたもの　８		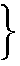→		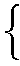10を単位としたもの　12 １を単位としたもの　18
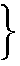138÷２		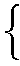10を単位としたもの　６ １を単位としたもの　９

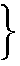したがって，138÷２＝69　となる。

　以上の計算の仕方は，84÷２，1.38÷２，８時４分÷２,１時38分÷２の計算に適用することができる。

　なお，小数で割る計算では1.38÷0.2，1.38÷２においては，除数が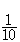であるから，結果は10倍にならなければならない。
 

0.69 ２）1.38 　　1 2 　　　18 　　　18 　　　 0

6.9 0.2）13.8 　　 12　 　　　18 　　　18 　　　 0

　このように考えても，商を求めることができるが，また，単位をそろえてから計算するというように考えても，商を求めることができる。。即ち，1.38は0.01の138倍であり0.2は0.01の20倍である。1.38，0.2をともに0.01を単位として考えてみれば，一方は138となり，他の方は20となる。したがって，138は20の何倍であるかを計算すればよいことになる。

　いろいろに考えて計算することはできるが，形式としては，今までにわかっている形式に帰着させることを考えられなくてはならない。即ち，小数を整数でわる計算がわかっているから，割られる数，割る数をともに0.1単位にして表わしていけばよいことに導くのである。

　分数についても同様である。例えば，



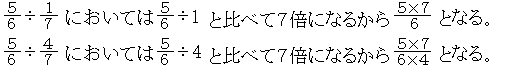
　これは，単位をそろえる考え方から，計算することもできる。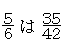

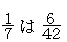　となる。したがって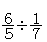，では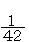，を単位と考えていけば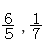はそれぞれ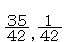したがって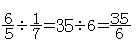となる。

　同様に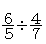では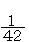，を単位とすれば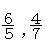，はそれぞれ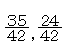となる。したがって，

　このようないろいろな形式のものを最も単純な形式にまとめる立場から，商が割られる数や割る数の分母・分子と，どんな関係にあるかを調べさせるがよい。

　

　このようにして，除法についての普通の形式が生まれてくるのてある。

　以上要するに計算過程の合理化ということは，種々の計算に一貫した考え方があることをわからせるように指導することである。子供は往々にして，十進数と諸等数の計算を別なものとして考えたり，小数や分数の乗法や除法を整数のそれと別々のもののように考えたりする。このように各種の計算が全く違った考え方によって行われるがために，考え方が混乱し，理屈をぬきにして形式的な計算になり，間違いを起すことになるのである。計算の仕方に一貫した考え方のあることを分からせることは，計算方法にも，形式にも，統一した理解を与えることになる。このように計算の仕方を把握しておれば，もし方法を忘れた場合でも，整数等の簡単な場合について考えれば，他をおし測ることができ，自分で考えつくことができるものである。

　このように忘れても苦にならない，はたらきとして理解されたものが身についた知識というものである。

　計算の合理化の基本他着眼は，すべての数の計算において，単位の観念を明確にし，数として把握させることである。例えば，分数の2/3を１個のリンゴを三等分したものが２つ集まっているというような，素朴な観念にこだわっていては，乗法や除法の意味の理解が困難となり，技能として計算も身につかないであろう。

⑨　計算において，よリよい方法を用いること

（一）　加法においては
78＋99＝(78＋100)−１＝178−１＝177

78＋49＝(78＋50)−１＝128−１＝127

　とするような方法を，場合に即して考えさせる。

（二）　減法においても，加法と同様に

157−99＝(157−100)＋１＝58

157−49＝(157−50)＋１＝107＋１＝108

（三）　乗法においては，次の如き方法が考えられる。
 

(１)　3.75×4.2を計算するのに，まず，3.75×42と普通に計算して，15750を得る。次に，整数部分３×４＝12を概算して15.75とする方法がある。

3.75 × 4.2 　 750 1500　 15.750

(２)　375×５＝(375×10)÷２＝1875

のように，５，25，125，をかける場合の簡単な計算方法も考えられる。

(３)　3.75×248の計算において
 

375 ×248 750・・・・・・375×２ 1500・・・・・750×２ 3000・・・・1500×２ 93000

375 ×248 　3000・・・・・375×８ 9000 ・・・・・3000×３ 93000　（24÷８＝３）

のような特殊な計算方法も考えられる。この場合に，部分積を乗数の真下に書くことの発展として，指導するがよい。

(４)　次に，375×99の計算において

375×99＝375×100−375

　　　＝37500−375

　　　＝37125

のように考える。375×98　375×999のようなものも同様に考えられる。

(５)　次に概算において

23×27≒25×25＝25÷４×100＝625

23×27≒20×30＝600

のように，被乗数と乗数の一方を切り捨てた時，他方を切り上げる等して，適当に按配して乗法を行う。これらの計算は生活に即して行わせるばかりでなく，他の計算に附隨して指導するがよい。仮商を立てたり，小数点の位置を定めたり，験算をしたりする場合に，繰り返し指導することが大切である。

(６)　分数計算においては

のような場合も考えられる。
（四）　除法においても，乗法と同じように，いろいうな方法が考えられる。
 

(１)　15.57÷37.5の計算において，これを整数として計算して4.2を得る。次に，15÷30＝0.5より15.75÷37.5＝0.42を得る。

4.2 375)1575 　　1500 　　　750 　750 　　　　0

(２)　485÷97の計算においては，485を500とし，97を100とみて，500÷100＝５とみて，仮商を立てさせるように指導する。

(３)　37÷５＝(37×２)÷10＝7.4

37÷25＝(37×4)÷100＝1.48

37÷125＝(37×８)÷1000＝0.296

のように５,25，125でわる簡単な計算方法も考えられる。

(４)　1375÷200では，次のような計算方法も考えられる。

(５)　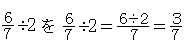とするような計算方法も考えられる。

計算においては，方法を固定せず，場合に応じて，更によりよい方法を生むように留意して指導すべきである。

　

　子供は，いろいろな場合に，力という言葉を使っている。このとき，何らかの方法で，その大小を直接にくらべたり，あるいは数字などで表わしたりして，間接にくらべたりする。力学で考える力についてもまた同様で，綱引とか，押し合うとかなどして，直接にくらべる場合もあれば，何キログラムの物を持ち上げる力などといって，間接にくらべる場合もある。

　力学で考える力についても，その大きさを力学的に定義してきめたものとして，子供に考えさせるべきではないであろう。持ち上げる力，引く力，あるいはそのような力におきかえたものとして，考えさせるべきであろう。いい換えれば，重さによって表わし，筋肉に訴えた感じで，その大きさを知ることのできるものとして，力の大きさを考えさせるべきである。この力の大きさの表わし方は，これは自然科学史を見ても明らかであるように，自然的発生的である。近代の力学における力の法則がまだわかっていなかったエジプト時代などに，ころやてこを用いて，重い物を引いたり，持ち上げたりしていたことからもわかる。したがって，力に対する指導もまた発生的・感覚的に行われなければならない。もし，観念的に行われたならば，数や量を抽象的に取り扱った場合と同じく，子供に興味もなく，実際生活に使えるものとはならないであろう。勿論筋肉に訴えられた力だけでは，その表現力が困難であり，記述の方法として，ベクトルが用いられるようになるのは当然である。要は力の指導は，子供が筋肉に訴えて知っている力から出発し，子供の直観を生かしながら行うがよい。そして，力を子供の身近な量として考えさせて，だんだん抽象化していくことを，心掛けねばならない。

　力学教材を取り扱う際には，とくに，次のことに注意をするがよい。

（一）　力の導入について

　力の観念及び力の大きさが子供に意識されるのは，力が足りないで，直接に重いものを持ち上げたり，動かしたりすることのできないときであろう。また，機械のはたらきが子供に意識されるのは，直接に動かすことのできないものを，機械を使って動かしているのを見て，驚異の念を起こす場合であろう。

　機械の働きを知るには，力の大きさを数で表わして，機械を使うとどんな大きな力が得られるかを調べなければならない。この必要から，まず，力の大きさを測る方法が考えられなければならない。

　義務教育においては，その測るものとして，ゴム秤あるいは手製のぜんまい秤などの程度のものでよいと考えられる。簡単な機械として，てこ・滑車・輪軸などについて，その働らきを明らかにする程度でよいと考えられる。

　子供の知識程度を考え，また，科学的な態度を養うことを目的とする教育であることを考え合わせれば，既成の力学法則を教えておいて，機械の働きを説明するのではなく，機械の働らきを調べた結果をとおして，力の間にある関係を帰納する態度でなければならない。

　てこ・輪軸・滑車等を取扱っていたのでは，力の大きさは意識されるが，力に向きのあることを考えねばならないことは，恐らく意識されないであろう。これは力の向きを考えないでよいとか，力の向きに気がつかないでいるとかいうのではない。機械が自らその方向を示したり，直観的に力の向きが明らかであったりして，力の向きを考えねばならないということが，子供の意識に上らないためであろう。力の向きを問題にしなくてはならなくなるのは，力を加えたとき，どの方向に物が動くかが，はっきりしないときである。物が動けばその方向に力が働らいていることは子供に容易にわかるであろう。したがって，幾つかの力を作用させて物が動くとき，それらの力の代りに，運動を止めさせるように，運動の方向と反対の方向に力をはたらかせて，その大きさと向きとか，始めの力の大きさと向きと，どんな関係にあるかを導いていけばわからせることができるであろう。

　この場合にも，抽象された力の合成・分解の法測を与えることなく，子供の経験から生み出してくるように，指導することを忘れてはならない。なお，はたらいている力の関係を明らかにして実験に移す際に，引く力は引いているものとし，押している力は押しているものとして測るのが，子供にはわかりやすい。しかし，実験の都合などで押す力を引く力て測ったり，引く力を押す力として測ったりすることがある。このような場合には，引く力と押す力との関係を十分に指導してから実験にとりかかるがよい。このような指導によって，力学における作用反作用についての秩序が別解されるであろう。

（二）　実験実測の際の指導

１．測定値に一々注意して取り扱うように指導すること。
　同じ実験あるいは測定を数回繰り返すと，一般に同じ値が得られないものである。しかし，条件を一定にしておけば，実験値はむやみに違うものでなく，大体似た値となる。したがって，もし，実験値としてそれまで測った値とかけ離れたものが得られたような場合には，何か特別な条件あるいは思わぬ誤差がはいっているときが多いから，その原因について一応たしかめてみるように指導すべきである。しかし，都合の悪い値が得られたからといって，その原因について吟味しないで，すぐに捨てるような習慣を付けないように注意すべきである。その原因について調べないでいると，実験の場合における条件を見落したままで実験を続けることになり，実験値は全くばらばらなものとなってしまうのである。実験実測にあたって，つねに，測定値に対して注意をしながら取扱うように指導すると，一々の操作を行うごとに，その条件をたしかめるような態度ができるし，往々にして，この特殊なものが大きな発見などのもとになることもある。
２．条件を明らかにし，それを一定に保つこと。
　力学の実験では，どんな条件の下に実験をしているのであるかということを，つねに念頭においていなけれはならない。とくに，繰り返えして測定をする場合には，その条件が，何時も同じように保たれるように，心がけねばならない。たとえば摩擦の実験をするときは，接触する二つの物体の種類は勿諭，接触する場所，特にゴム秤をかける場所や引き出すときの力のかけ具合などを一定に保つように，注意しなければならない。要すれば，位置などは線を引いて決めておくがよい。また，人によって，測定値を大き目に読む人と，小さ目に読む人とがある。このような避けられないものは，できるだけ多くの人の実験値をとりまぜて，その個人の避けられない誤差を，できるだけ除くようにしなければならない。
３．測定値から代表値を選ぶときの注意。
　測定値が得られたならば，それから代表値を決めることが問題となる。上にあげたことがらに，十分注意して行った実験から得た値は，すべて同等であると考えられる。したがって，その代表値を決める方法としては，義務教育の程度で栢加平均をとる程度でよいと思う。この場合に，実験値の正確度が揃うように，有効数字の個数について注意しなければならない。即ち，４回の測定で12.4㎝，12.3㎝，12.6㎝，12.4㎝が得られたとき，この平均12.425㎝を代表値として採ってはならない。この測定値では，0.1cmの程度の正確度しか保証されないのであるから，12.425cmとして終りの５まで保証することはできないわけである。したがって，代表値として12.4cmをとるのが適当である。
４．一段々々に見透しを持つこと。
　ある一つのことがらを調べるときに，条件をいろいろに変えて実験しなければならないことがある。このようなときには，なるべく各段階毎に実験値を処理させて，次の段階に対する見透しを持たせるがよい，先きの見透しを持っていれば，変えるように意図した条件のみが変っているか，また，変えないようにと考えていた条件を見落しているのではないかという反省ができるからである。

　しかし，この見透しはどこまでも暫定的なものであって，次の実験によってくつがえされるかも知れない運命をもっているものである。したがって，見透しは持ちながら，どこまでも忠実に実験を見守る態度を養わなくてはならない。いやしくも，その見透しを固守するために，実験値をことさらに大きく，あるいは小さく読むようなことがあってはならない。

５．グラフを作るときの注意
　実験の結果について，それらの間にある関係を見出すとき，数値の表によるよりも，一応グラフにまとめた方が見易い場合がある。

　測定値を記入した点から，その実験の結果をまとめるために曲線を推定するとき曲線がそれらの点を均等に分けるようにしなければならない。これは測定値に対して平均をとるのと同じような考え方である。

　あまりかけ離れた点があるような場合には，その点を決めるもとになっている測定値ついて，吟味をしてみる必要がある。これは，測定値について述べたときと同じである。また，グラフが直線であると推定されるようなときに，始めの点と終りの点を直線で結んで他の点を一こう省みない場合がある。これについても上にのべた観点から十分に注意して指導すべきである。

⑪　極限の観念を明らかにすること

　極限の観念は，我々の日常生活において，無意識的に用いられている。これを数学的に見直し，その観念の理解を深かめるようにしなければならない。

　極限の観念については，昔から有名なアキレスとかめの問題，アルキメデスの求積あるいは正方形の対角線を有理数で表わそうとした問題などがある。最初これ等はいずれも，極限の存在を仮定して解決したか，あるいは極限の存在について懐疑の目を向けたのみであった。その後，極限があるかないかが問題となり，その存在を仮定することは厳密性をかくことに気が付き，極限の存在自身についても考えられ始めた。しかし，義務教育程度の子供で，極限の存在を問題にするのは，恐らく無理なことであろう。このようなことは，子供の智能の程度を超え，子供の興味を減じ，子供にとって不自然なことである。故に，直観的に極限の存在を仮定し，その極限を用いて，色々なことがらを処理する程度に，その指導を止めるのがよいであろう。

（一）　数・量について

　数を表わす場合に，単位を10，100，1000，…と大きくすることによって，如何程でも大きな数を表わすことができる。また，単位を0.1，0.01，0.001，……と小さくすることによって，如何程でも小さな数を表わすことができる。

　1/3などの分数を小数に直すときに，小数点以下のけた数を多くすればするほど，如何程でも詳しく書くことができる。しかし，３をいくら書き続けても1/3に等しい小数を書くことはできない。0.3という記号によって，限りなく書き続けられたものを書き表わすのである。これに極限の観念がある。

　また，長さや重さなどの量を測定する場合にも，同じようなことがいえる。物の重さや長さなどを，われわれは観念的に考えることができる。しかし，これをそのままにしておいたのでは，処理することができない。どうしても，測ることをしなければならない。測り方を精巧にすればする程，詳しい値が得られる。このようなことを考えれば，素朴な考えとしての長さや重さなどの量も，測定値とくらべて考えれば，観念的には極限につながるものである。

　また，観念として持っている長さをもとにして，面積や体積を計算しようとしても，計算することができない。強いて計算しようとすれば，どうしても実際の数値である測定値に頼るほかはない。ここに，測定値の取り扱いの大切な点がある。即ち，正確度を要求している面と，適当な正確度をもって表現しなければならない宿命的な面がある。この二つの面の矛盾を打開し，目的に応じた正確さで処理していくところに，測定値・近似値の取り扱いの困難な点がある。

　極限の観念を明らかにさせるためには，以上の観点を十分に理解して，指導しなければならない。

（二）　形について

　複雑な図形は，正方形や立方体をもとにして構成されると考えられる。なお，この場合に，それを構成するための正方形や立方体の大きさを次第に小さくしていけば，どれだけでもその形に近いものができると考えられる。これは積み木でいろいろなものを作ったり，また円の面積を方眼から読みとろうとするときに，考えられることである。いいかえると，正方形や立方体は図形を構成する時において，単位であると考えられるものである。このように考えてはじめて，複雑な図形の面積や体積などを測ることができるのである。